문제 링크
https://www.acmicpc.net/problem/2133
문제 유형
DP
🌈문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
2출력
첫째 줄에 경우의 수를 출력한다.
3💡 아이디어
항상 DP문제를 풀 때 점화식을 세우려는 노력을 해야 하는데 나는 아직 그 부분이 부족한 거 같아서 그림으로 해결하려는 습관을 해결해야 할 것 같다.
점화식 세우기는 항상 어려운데 이문제는 도가 지나치게 어려웠다.^^ 하
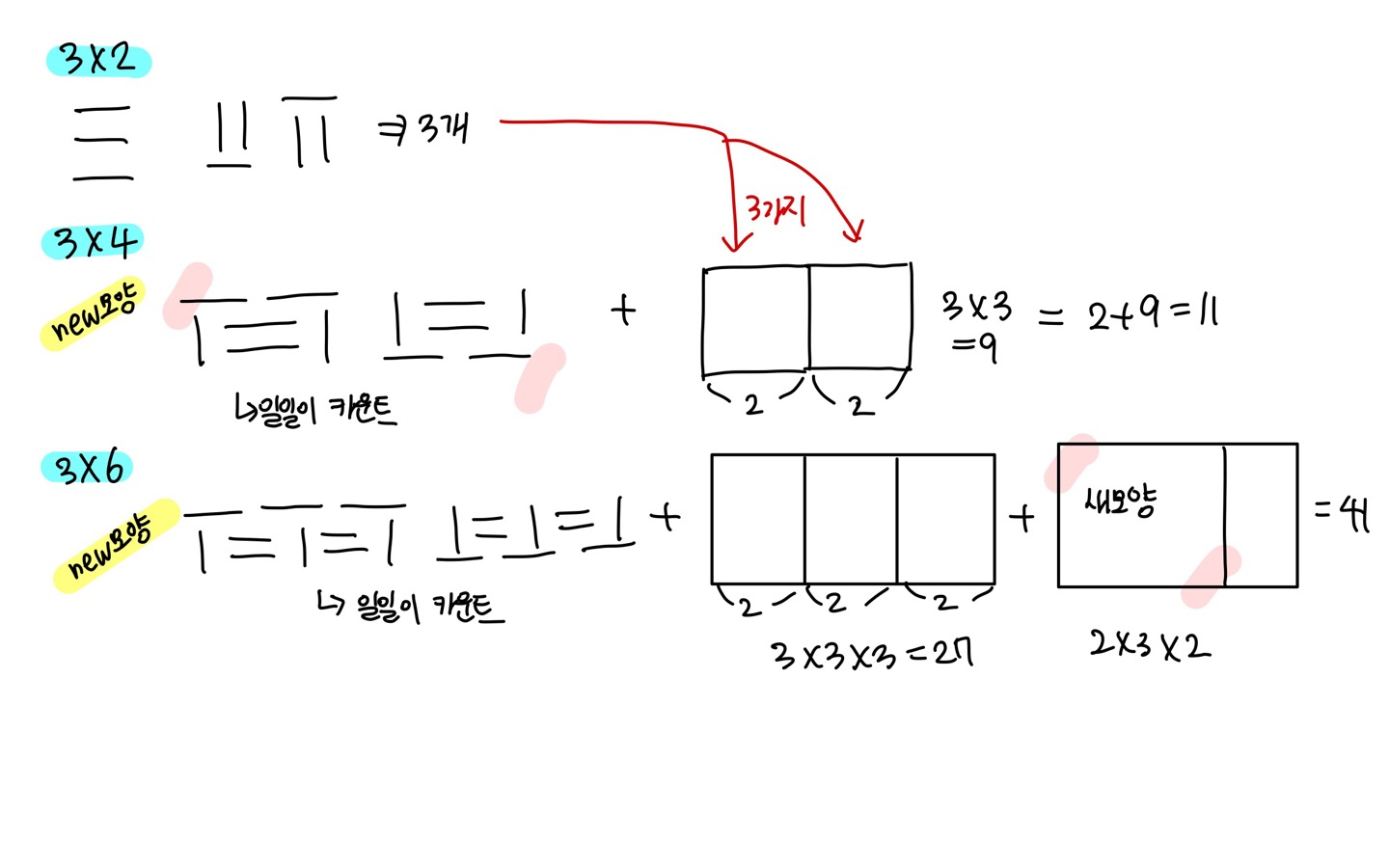
확인해야 하는 규칙은 다음과 같다.
1. 짝수만 경우의 수가 존재한다.
2. 한 단계씩 늘어날 때마다 새로운 모양이 2개씩 추가되므로 더해 주어야 한다.
3. 중간에 새롭게 생긴 모양에 대한 (2가지에 대한) 조합을 생각하기
새롭게 생긴 모양과 남은 자리에 대한 조합을 생각해야 하기 때문에 dp[6]을 구한다면 dp[2] x 2, 을 추가로 더해주고, dp[8]을 구한다면 dp[4] x 2, dp[2] x 2를 추가로 더해주어야 한다는 것이다. 이것은 n-4~2까지 시그마의 합으로 더해준다면 공식이 완성된다.
정말 매우매우 어려운 점화식 세우기이고 이해하기에도 많은 시간이 들었다.
👨💻 코드 작성
N = int(input())
d = [0]*31
d[0] = 1
for i in range(2, N+1, 2):
d[i] = d[i-2] * 3
for j in range(0, i-2, 2):
d[i] += d[j] * 2
print(d[N])코드는 매우 간단하다.
dp는 점화식을 정말 잘 세워야 하는 거 같다!! ㅜㅜ

논리에 문제는 없는데, 새로운 모양의 그림이 틀린 것 같습니다.
| = = | ㅡㅡㅡ
ㅡㅡㅡ | = = | <-- n = 6
| = = = | ㅡㅡㅡㅡ
ㅡㅡㅡㅡ | = = = | <-- n = 8 ...
이런 식으로 가운데 작대기가 사라져야 차원이 맞는 것 같습니다.