
문제 링크
https://www.acmicpc.net/problem/2294
문제 유형
DP (다이나믹 프로그래밍)
🌈문제
n가지 종류의 동전이 있다. 이 동전들을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그러면서 동전의 개수가 최소가 되도록 하려고 한다. 각각의 동전은 몇 개라도 사용할 수 있다.
사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.
입력
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다. 가치가 같은 동전이 여러 번 주어질 수도 있다.
3 15
1
5
12출력
첫째 줄에 사용한 동전의 최소 개수를 출력한다. 불가능한 경우에는 -1을 출력한다.
3💡 아이디어
엇, 그리디다.라는 생각이 먼저 들었는데, 이 문제는 그리디로 풀게 되면 틀리게 된다. 그리디의 생각을 한번 적용해보자면,
가장 가치가 큰 12를 무조건 사용해야 하고, 12를 사용하게 되면 1을 3번 더 사용하게 되어서 답이 4가 도출된다.
그러나 이 문제는 3이 답이고, 그리디를 사용한 결과 틀리게 되는 것이다.
그렇다면 완전탐색은 어떤가? 완전탐색으로는 3개의 동전을 수가 채워질때까지 확인하는 과정이 존재하여 최소 2의 15승이 도출되어 시간초과가 나게 될 것이다. 그렇게 하여 도출될 수 있는 것이 바로 DP인 것이다. 모든 경우를 한번 다 따져보자.
dp테이블이 어떤 역할을 하는지 정의를 해보자.
DP 테이블은 dp[i] = i원을 만드는 데 필요한 동전 개수라고 정의한다.
직관적으로 생각해본 dp 테이블의 모양은 아래와 같다.

이제 점화식을 찾아보도록 하자. 이 부분이 가장 어렵고 DP를 풀 때 까다로운 점이다.
DP 테이블을 초기화해야하는데, 해당 문제가 가질 수 있는 k의 값의 최대값은 10,000원이므로, MAX값은 만보다 1 큰 10,001로 잡아둔다.
초기화를 완료하였으니 어떤 로직으로 해당 테이블을 채워 나갈 것인지에 대해 로직을 생각해보면 되는데, 먼저 1원으로 채울 수 있는 금액은 모두 채운다. 이후,5원을 사용하였을 때 기존 1원을 사용하였을 때의 동전 개수보다 적게 사용되는 친구들이 있다면 그 값으로 DP테이블을 갱신하면 되는 것이다.
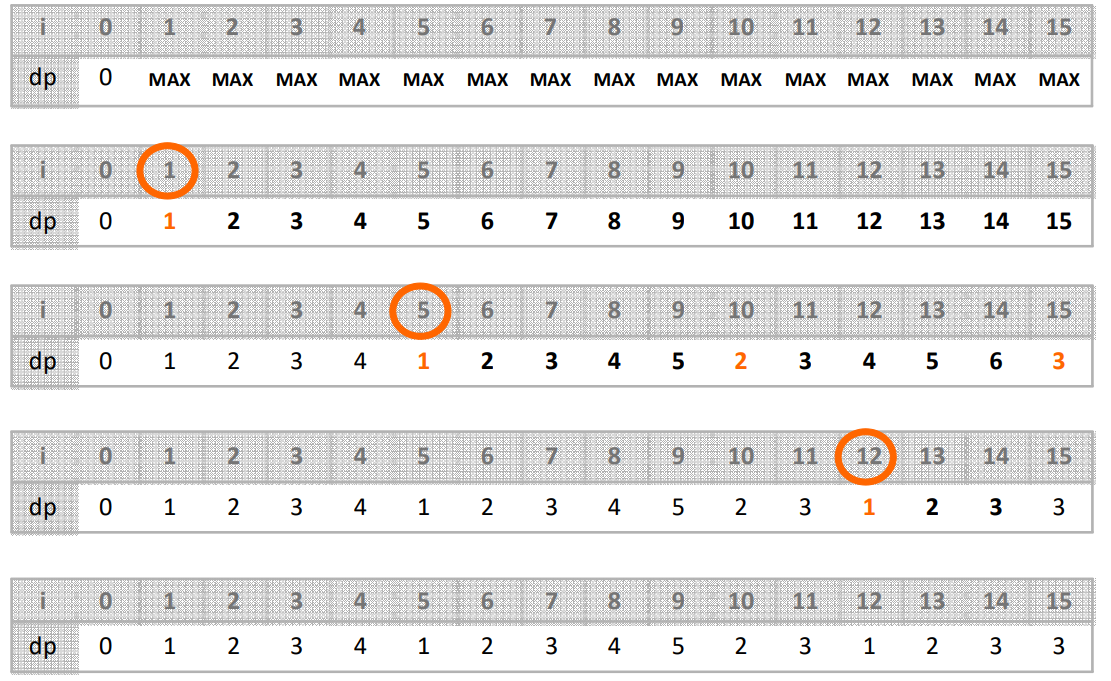
최소값을 이용하여 갱신을 쭉쭉 해준 모습이다. 처음 1원만 이용하였을 때, 5원을 이용하였을 때, 12원을 이용하였을 때의 모습이다.
그럼 그 이후 최소값 갱신은 어떻게 하나?
12원을 사용할 때를 보자. 13원을 만들고자 하면 13 - 12 = 1이고, 이전에 사용하였던 1원에 대해 사용한 동전 개수를 더해주면 된다. 그 이유는 앞서 존재하는 1~12원까지의 동전 개수가 최소 개수로 이미 갱신된 것이므로 이것을 이용하는 것이다.
그럼 MAX값으로 10,001을 잡는 이유는 무엇일까? 10,000원은 왜 안될까?
동전을 10,000개 사용하는 경우 최대값으로 판단하고 올바르게 출력해야 하는 로직을 세워야 하는데, MAX값을 10,000으로 잡게되면 오류가 발생하게 된다. 동전을 10,000개 사용하는 경우와, 10,001개 사용하는 경우를 구분하기 위하여 1을 더해놓은 것이다.
👨💻 코드 작성
코드는 다음 순서로 작성한다.
1. DP테이블 정의 : dp[i] = i원을 만드는 데 필요한 동전의 최소 개수
2. 점화식을 정의한다. dp[i] = min(dp[j], dp[j - coin[i] ] + 1)
dp[j]는 원래 채워진 값이고, dp[j - coin[i]] +1은 13 - 12원 1의 값에다가 1을 더한 값으로 갱신을 해주는 과정이다.
3. 초기값 설정 : dp[0] = 0, dp[i] = MAX + 1
n, k = map(int, input().split())
#최대 동전 종류 개수 100개까지 들어갈 수 있음
coin = [0 for i in range(101)]
dp = [10001 for i in range(k + 1)]
#dp값 MAX로 초기화, 단, MAX값에서 하나 더한 값으로 초기화
dp[0] = 0 #첫번째 dp는 0으로 정의
# 나머지 입력값 차례로 받음
for i in range(n):
coin[i] = int(input())
for i in range(n): #동전 개수까지만 검사!
coinD = coin[i] # 현재 어떤 동전의 가치를 확인하고 있는지 j에다가 시시각각 저장합니다.
for j in range(coinD, k + 1): #coin원부터 검사시작합니다. 이미 앞에 있던 친구들은 검사 끝났다..
dp[j] = min(dp[j], dp[j - coin[i]] + 1)
if dp[k] == 10001:
print(-1)
else:
print(dp[k])일차원 배열로 푸는 풀이인데, DP는 2차원 배열로 많이 푸니까 그것으로 도전해봐도 좋을 거 같다.
