[BOJ] 9251번 - 최장 공통 부분 수열 LCS알고리즘

김유진·2023년 1월 14일

DP boj

PS

목록 보기

12/36

문제 링크

https://www.acmicpc.net/problem/9251

문제 유형

DP (다이나믹 프로그래밍)

🌈문제

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

입력

첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.

ACAYKP
CAPCAK

출력

첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를 출력한다.

💡 1. 아이디어

DP로 풀어야 하는 이유부터 생각을 해보자.
먼저 완전 탐색으로 풀었을 때 무슨 문제가 있길래 DP를 가져와서 풀어야 하는 것일까?
N개의 주어진 문자열을 선택하거나, 선택하지 않거나 두가지 경우가 존재하고, 그 개수를 직접 세어보면 된다.
즉 나올 수 있는 수로는 O(2^n x 2^n x N) 되며.. 엄청나게 큰 수가 발생하여 완전탐색은 불가능하다는 것을 확인할 수 있었다.
그렇다면 DP를 이용하여 풀게 되면 어떻게 해야 할까..

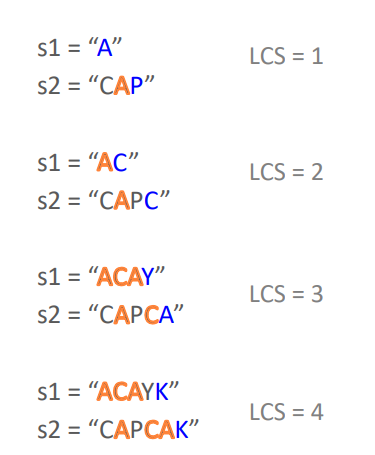
가지고 있는 공통 배열을 나열해서 하나씩 차례대로 보면,
s1에서 가져온 값과 s2에서 가져온 값을 비교해 볼 수 있을 것이다.
직관적으로 LCS가 최대 4가 될 수 있다는 것을 이해할 수 있다.

그런데, 이 LCS값을 더하는 기준을 어떠게 할 것인가?가 이 문제의 어려운 포인트라고 할 수 있는 것 같다.

1) 만약 LCS 끝의 두개의 문자열이 같은 경우

K로 같기 때문에 전 단계의 문자열을 비교하고 같은 것이 겹치는 것끼리를 계산하여 LCS에다가 1을 더하면 된다.

2) 만약 LCS 끝의 두개의 문자열이 같지 않은 경우

예시로 들 수 있는 상황은 아래와 같은 상황이다.
ACAY
CAPCA
첫번째 시도로는 두번째 배열의 A를 제거해보고 일치하는 문자열 개수를 찾아본다. 그러면 ACA와, AC가 존재하므로 LCS 값이 2가 된다.
두번째 시도로는 첫번재 배열의 Y를 제거해보고 일치하는 문자열의 개수를 찾아본다. ACA, ACA 두개가 존재하므로 LCS값은 3이 된다. 이 둘 중에 Max값을 찾아 정답으로 내놓으면 된다.

👨‍💻 2. 코드 작성

코드는 아래의 순서로 작성할 수 있다.

1) DP테이블을 2차원으로 작성한다. dp[i][j]로 작성하되, i는 첫번째 문자열의 길이, j는 두번재 문자열의 길이이다.

2) dp[i][j]에서

s[i] == s[j] 일때, 전의 LCS값에서 1을 더한다.
s[i] != s[j] 일때, dp[i-1][j]와 d[i][j-1] 값 중에서 더 큰 값을 선택한다.

import sys

read = sys.stdin.readline

# 두개의 문자열을 받아온다.
s1, s2 = read().strip(), read().strip()

# s1, s2를 행과 열로 삼아 dp 2차원 테이블을 만든다.
dp = [[0 for j in range(len(s2) + 1)] for i in range(len(s1) + 1)]


for i in range(1, len(s1) + 1):
    for j in range(1, len(s2) + 1):
        if s1[i - 1] == s2[j - 1]:
            dp[i][j] = dp[i - 1][j - 1] + 1
        else:
            dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

# 가장 마지막 행 출력!
print(max(max(dp)))