이진 탐색 트리(binary search tree)란?
- 이진 트리 기반의 탐색을 위한 자료 구조이다.
- 예) 전화번호 찾기, 사전에서 단어 찾기 등
이진 탐색 트리 탐색
- 컴퓨터 프로그램에서 탐색은 레코드(파일을 액세스 할 때 실제로 읽고 쓰는 단위)의 집합에서 특정한 레코드를 찾아내는 작업을 의미한다.
- 레코드는 하나 이상의 필드(field)로 구성된다.
- 레코드들의 집합을 테이블(table)이라 하고 레코드들은 보통 키(key)라고 불리는 하나의 필드에 의해 식별할 수 있다.
- 다른 키와 중복되지 않는 키인 주요키(primary key)로 특정한 키를 가진 레코드를 찾는다.
이진 탐색 트리의 정의
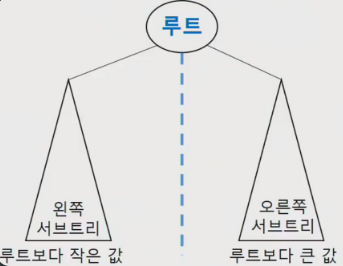
- 모든 원소의 키는 유일한 키를 가진다.
- 왼쪽 서브 트리 키들은 루트 키보다 작다.
- 오른쪽 서브 트리의 키들은 루트의 키보다 크다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
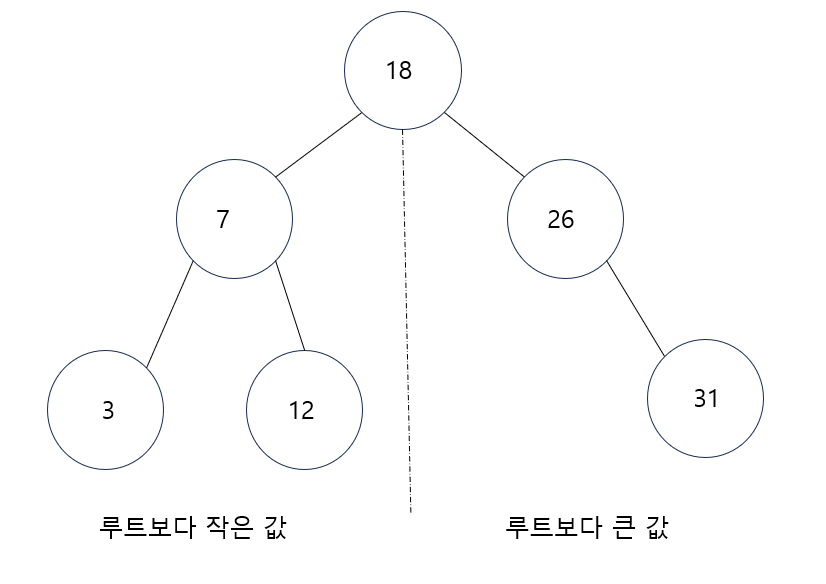
이진 탐색 트리의 성질
-
찾고자 하는 키값이 이진트리의 루트 노드의 킷값과 비교하여 루트 노드보다 작으면 원하는 키값은 왼쪽 서브트리에 있고 루트노드보다 크면 원하는 키값은 오른쪽 서브트리에 있다.
-
이진 탐색 트리를 중위순회 방법으로 순회하면 오름차순 정렬이 된다.
순환적인 탐색연산 알고리즘
- 이진 탐색 트리에서 특정한 키값을 가진 노드를 찾기 위해서는 주어진 탐색키 값과 루트 노드의 키값을 비교한다.
- 비교한 결과가 같으면 탐색이 성공적으로 끝난다.
- 비교한 결과가, 주어진 키 값이 루트 노드의 키값보다 작으면 탐색은 이 루트 노드의 왼쪽 자식을 기준으로 다시 시작한다.
- 비교한 결과가, 주어진 키 값이 루트 노드의 키값보다 크면 탐색은 이 루트 노드의 오른쪽 자식을 기준으로 다시 시작한다.
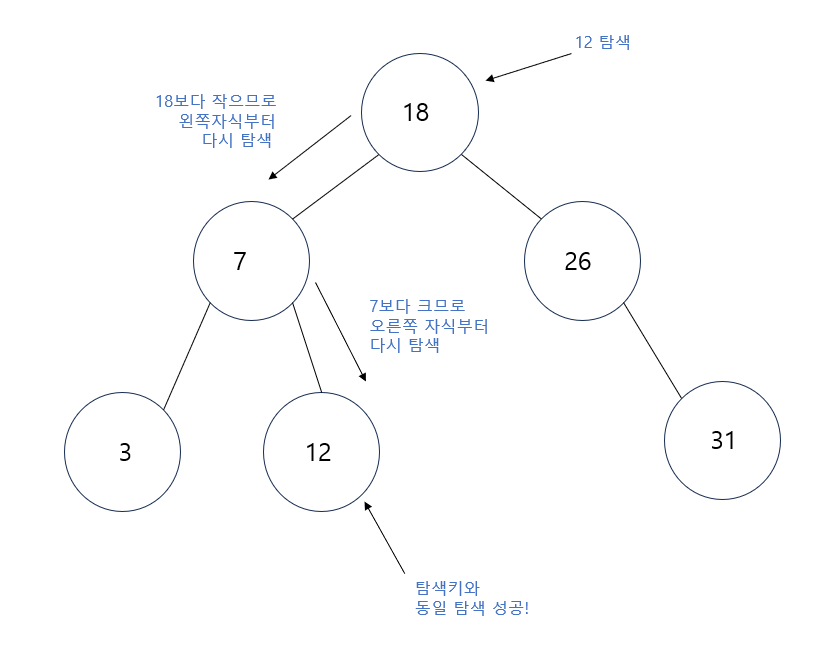
- 순환적인 탐색함수에 대한 코드는 다음과 같다.
//순환적인 탐색 함수
Treenode * search(TreeNode * node, int key)
{
if (node == NULL) return NULL;
if (key == node->key) return node;
else if (key < node->key)
return search(node->left, key);
else
return search(node->right, key);
}반복적인 탐색연산 알고리즘
- 매개변수 node가 NULL이 아니면 반복을 계속한다. 반복 루프 안에서는 현재 node의 키값이 key와 같은지 검사한다.
- 같으면 탐색 성공으로 현재 노드 포인터를 반환.
- 만약 key가 현재 노드 키값보다 작으면 node변수를 node의 왼쪽 자식을 가리키도록 변경
- 만약 key가 현재 노드 키값보다 크면 node변수를 node의 오른쪽 자식을 가리키도록 변경
- 이러한 반복은 node가 결국 단말노드까지 내려가서 NULL값이 될 때까지 반복한다.
- 반복적인 탐색함수에 대한 코드는 다음과 같다.
// 반복적인 탐색 함수
TreeNode * search(TreeNode * node, int key)
{
while (node != NULL) {
if (key == node->key) return node;
else if (key < node->key)
node = node->left;
else
node = node->right;
}
return NULL; // 탐색에 실패했을 경우 NULL 반환
}이진 탐색 트리 삽입연산
- 원소를 삽입하기 위해서는 먼저 탐색을 수행하는 것이 필요
- 이유는 이진 탐색 트리에서는 같은 키값을 갖는 노드가 없어야 하기 때문이고 또한 탐색에 실패한 위치가 새로운 노드를 삽입하는 위치가 되기 때문이다.
- 새로운 노드는 항상 단말노드에 추가된다.
- 단말 노드를 발견할 때까지 루트에서 키를 검색하기 시작하고 단말 노드가 발견되면 새로운 노드가 단말 노드의 하위 노드로 추가된다.
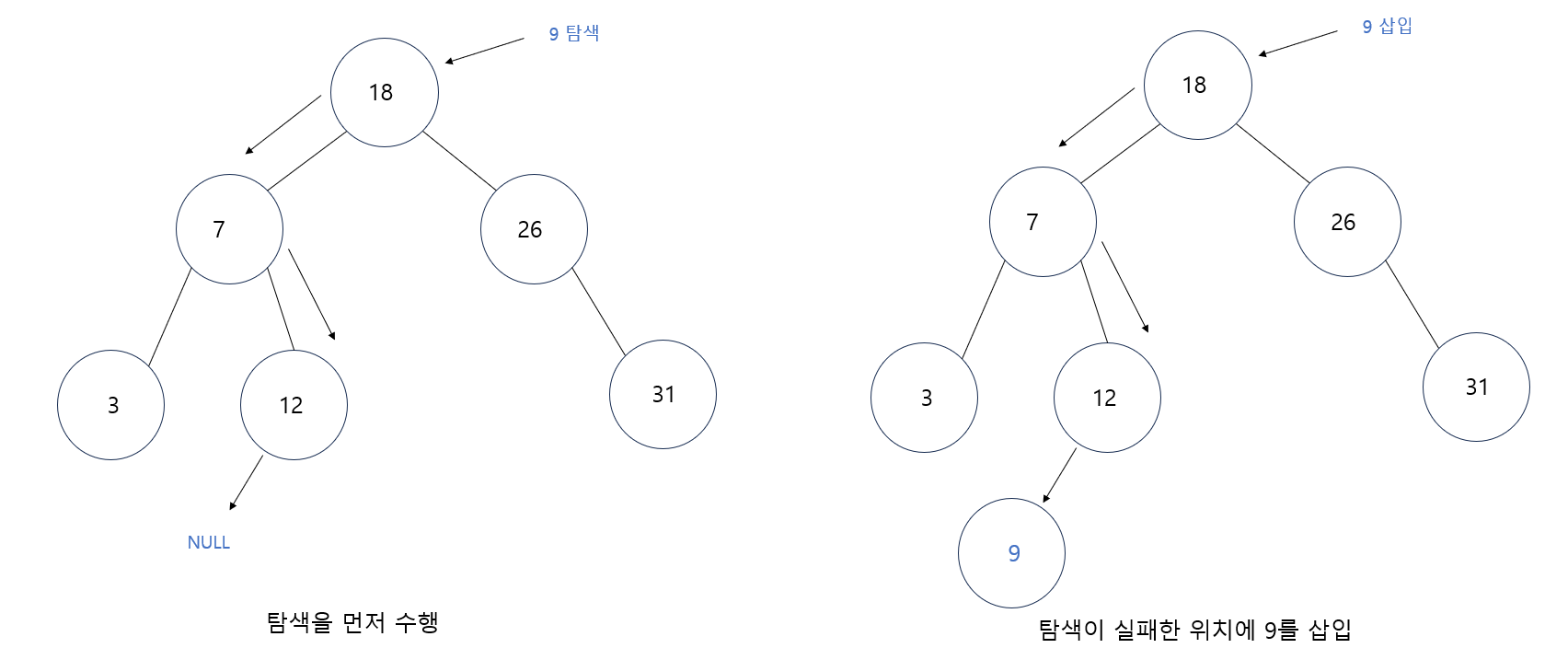
- 먼저 9를 삽입하기 이전에 루트에서부터 9를 탐색해 본다.
- 탐색이 성공하면 이미 9가 트리 안에 존재하는 것이고, 키가 중복되므로 삽입이 불가능하다.
- 만약 9가 트리 안에 없으면 어디선가 탐색이 실패로 끝날 것이고 그 위치가 9가 삽입 될 곳이다.
- 이진트리 삽입에 대한 코드는 다음과 같다
TreeNode * insert_node(TreeNode * node, int key)
{
// 트리가 공백이면 새로운 노드를 반환한다.
// new_node는 새로운 노드를 연결하는 함수이다.
if (node == NULL) return new_node(key);
//그렇지 않으면 순환적으로 트리를 내려간다.
if (key < node->key)
node->left = insert_node(node->left, key);
else if (key > node->key)
node->right = insert_node(node->right, key);
// 변경된 루트 포인터를 반환한다.
return node;
}이진 탐색 트리 삭제연산
- 삭제는 다음의 3가지 경우를 고려하여야 한다.
- 삭제하려는 노드가 단말 노드일 경우
- 삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리중 하나만 가지고 있는 경우
- 삭제하려는 노드가 두개의 서브 트리 모두 가지고 있는 경우
첫 번째 경우 : 삭제하려는 노드가 단말 노드일 경우
- 단말 노드만 삭제하면 된다.
- 단말 노드의 부모노드를 찾아서 부모노드안의 링크필드를 NULL로 만들어서 연결을 끊으면 된다.
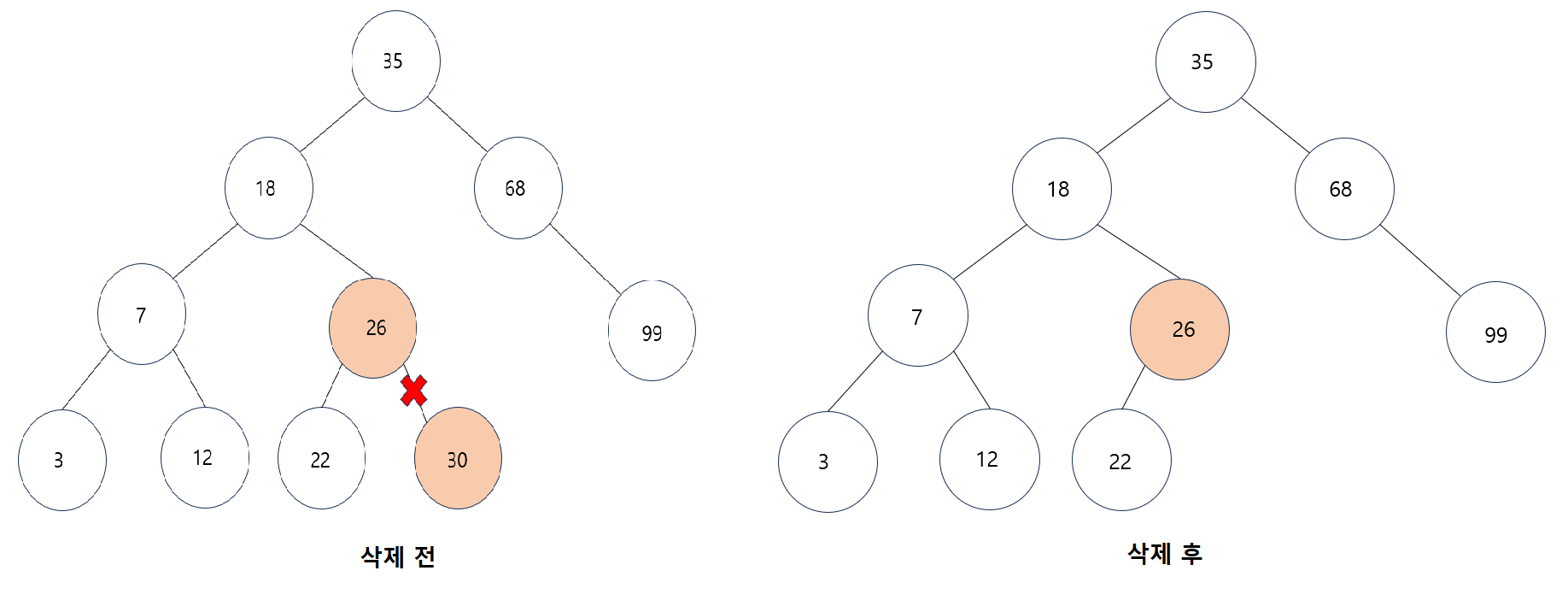
두 번째 경우 : 삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리중 하나만 가지고 있는 경우
-
자신 노드는 삭제하고 서브 트리는 자기 노드의 부모 노드에 붙여주면 된다
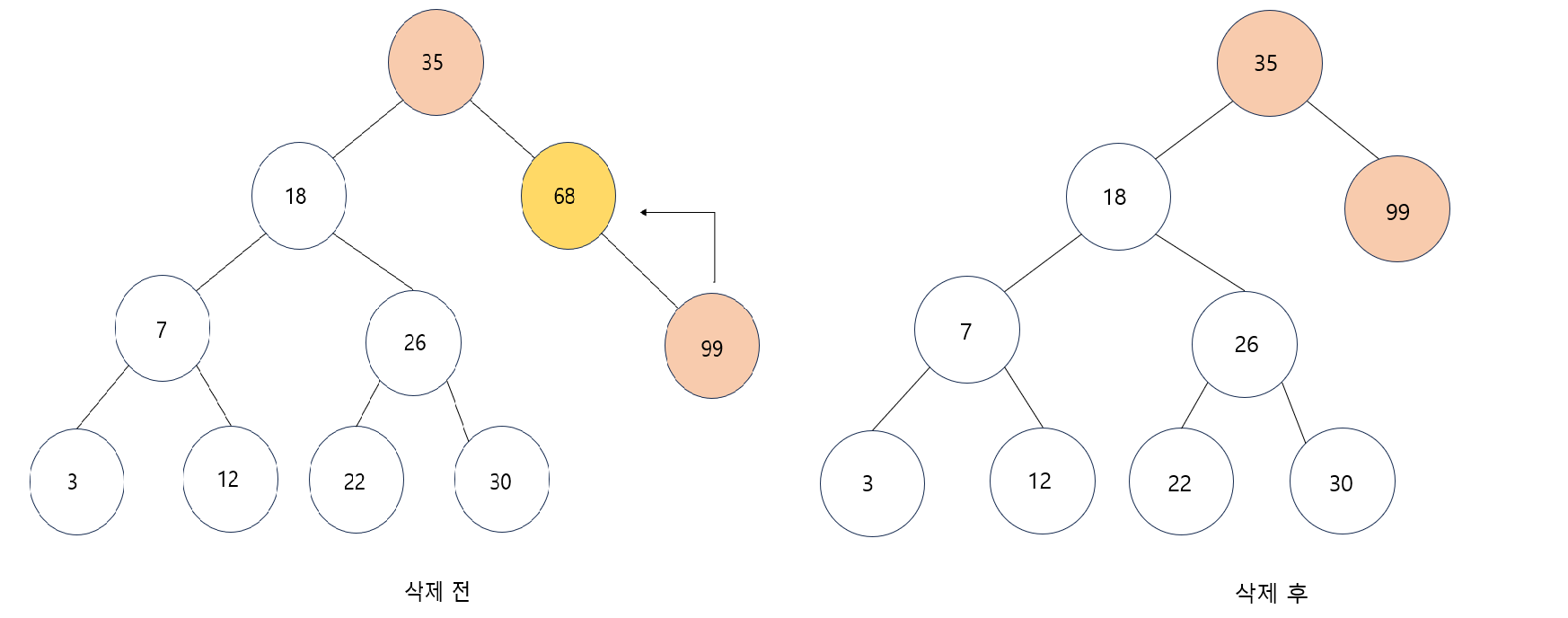
세 번째 경우 : 삭제하려는 노드가 두개의 서브 트리 모두 가지고 있는 경우
- 삭제되는 노드와 가장 값이 비슷한 노드를 후계자로 선택해야 한다.
- 왼쪽 서브트리에서 가장 큰 값이나 오른쪽 서브트리에서 가장 작은 값으로 선택
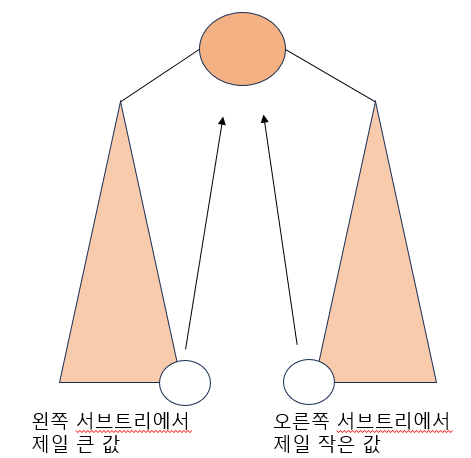
- 삭제노드가 18이라고 하였을 경우, 후계자가 될 수 있는 대상 노드는 아래와 같이 12와 22가 된다.
- 둘 중 어느 노드를 선택하여도 상관이 없다.
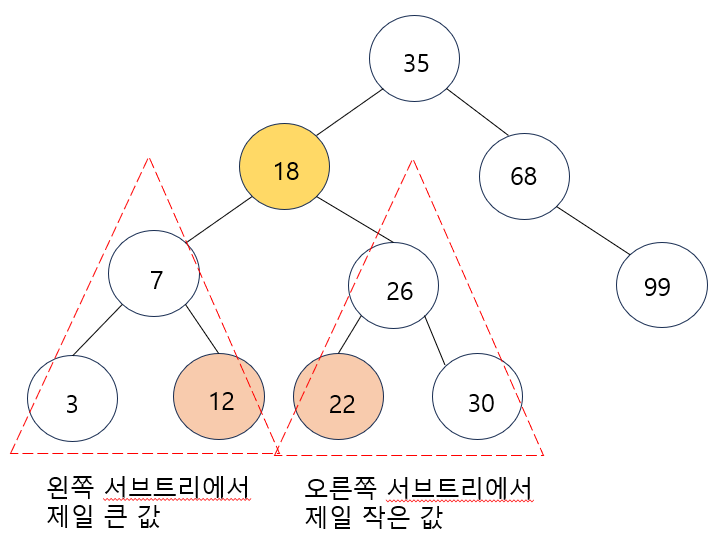
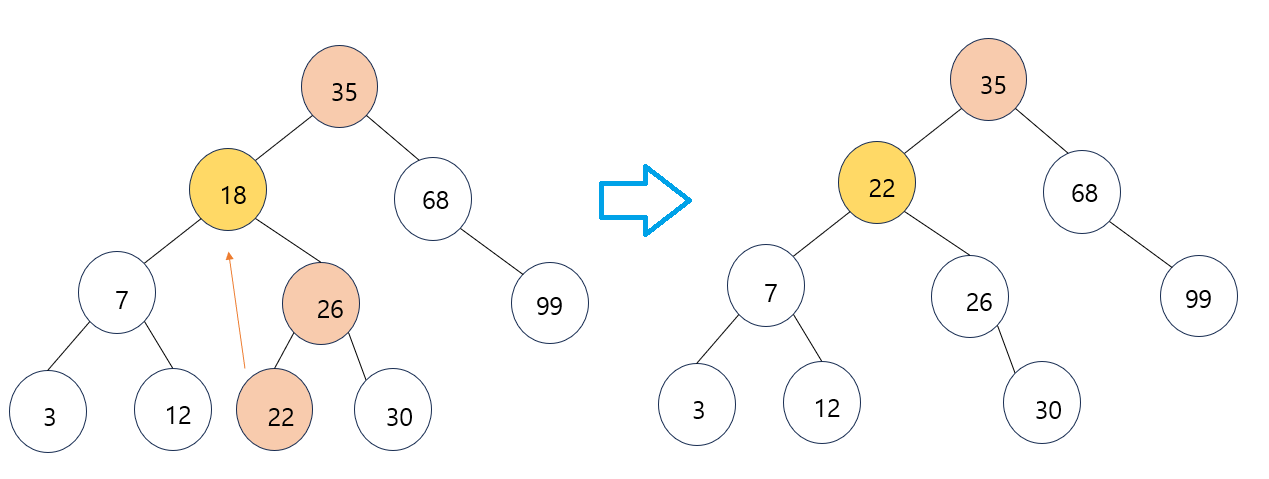
- 오른쪽 서브트리에서 제일 작은 값으로 선정하게 되면 22가 18자리로 이동하게 된다.
- 이진 탐색 트리에서의 삭제 함수에 대한 코드는 다음과 같다.
// 이진 탐색 트리와 키가 주어지면 키가 저장된 노드를 삭제하고
// 새로운 루트 노드를 반환한다.
TreeNode * delete_node(TreeNode * root, int key)
{
if (root == NULL) return root;
// 만약 키가 루트보다 작으면 왼쪽 서브 트리에 있는 것임
if (key < root->key)
root->left = delete_node(root->left, key);
// 만약 키가 루트보다 크면 오른쪽 서브 트리에 있는 것임
else if (key > root->key)
root->right = delete_node(root->right, key);
// 키가 루트와 같으면 이 노드를 삭제하면 됨
else{
// 첫 번째나 두 번째 경우
if (root->left == NULL){
TreeNode * temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL){
TreeNode * temp = root->right;
free(root);
return temp;
}
// 세 번째 경우
//min_value_node 함수는 최소 키값을 가지는 노드를 찾아서 반환해주는 함수임
TreeNode * temp = min_value_node(root->right)
// 중위 순회시 후계 노드를 복사한다.
root->key = temp->key;
// 중위 순회시 후계 노드를 삭제한다.
root->right = delete_node(root->right, temp->key);
}
return root;
}이진 탐색 트리의 분석
- 이진 탐색 트리에서의 탐색, 삽입, 삭제 연산의 시간 복잡도는 트리의 높이를 h라고 했을 때 가 된다.
- n개의 노드를 가지는 이진 탐색 트리의 경우, 일반적인 이진 트리의 높이는 이므로 이진 탐색 트리의 연산의 평균적인 경우의 시간 복잡도는 이다.
- 최악의 경우에는 한쪽으로 치우치는 경사 트리가 되어서 트리의 높이가 n이 된다
- 최악의 경우에는 탐색, 삭제, 삽입시간이 O(n)이 된다.