해당 시리즈는 LG에서 지원하는 LG Aimers의 교육 내용을 정리한 것으로, 모든 출처는 https://www.lgaimers.ai/ 입니다.
casual inference은 인과성에 대한 소개와 인과적 추론을 하기 위한 기본 개념이다.
Casuality
casuality는 하나의 어떤 무언가가 다른 무엇을 생성함에 있어 영향을 미치는 부분적인 관계를 말한다.
이는 즉, 원인과 결과 사이의 관계는 필요조건이나 충분조건일 필요가 없다는 말이다.
예를 들어 '버스를 놓쳐서 지각을 했다' 라는 문장이 있으면, 이는 인과적 관계를 보인다.
Science는 일반적 사실이나 법칙을 포함하는 지식체계로 정의하며, 여기서 법칙은 현상의 본질적인 구조를 명확하게 한 것을 의미한다.
과학에서 물리나 화학과 같은 자연과학과 함께 심리학, 경제학과 같이 실험하기 어려운 사람, 사람 집단의 행동에 대한 연구하는 것들은 단순히 상관관계를 찾는 것이 아니라, 인과관계를 밝혀야 한다.
Artificial Intelligence는 s/w나 로봇과 같은 에이전트가 목표를 성취하게 하기 위해 합리적인 액션을 취하는 것을 의미하는데, 이는 환경에 변화를 주어 원하는 상태로 변화시키는 인과관계로 해석이 가능하다.
비슷한 개념인 Machine Learning에서는 데이터간의 상관성을 학습한다.
Data Science에서는 데이터를 수집하고 처리하고, 분석해서 나온 결과를 어떻게 소통, 설명할 것인가 하는 부분에서 상관성 및 인과성을 복합적으로 고려한다.
Casual Hierarchy
3개의 레벨이 존재한다.
level 1: 가장 기본적인 관측 계층으로, 시스템을 구성하는 어떤 변수들의 상관성을 알 수 있다.
예를 들어, 데이터에 아스피린 약을 먹은 사람과 먹지 않은 사람이 있을 때, 그 사람들의 두통이 어땠는지 단순하게 비교하는 것이 level 1의 목적이다.
level 2: 실험계층으로, 연구를 하고자하는 시스템을 실험하여 나온 결과에 관심이 있다.
예를 들어, 아스피린을 두 그룹에 무작위로 먹게 한 후, 그룹 사람들의 두통이 어떤 식으로 바뀌었는가 하는 것들이 있다.
level 3: 관측 값과 실험에 의한 값을 동시에 고려하는 반사실적 계층이다.
예를 들어, 아스피린을 먹고 두통이 사라진 경우, 만약 아스피린을 먹지 않았더라면 두통은 어떻게 변했을까 하는 질문에 답을 하는 것이다.
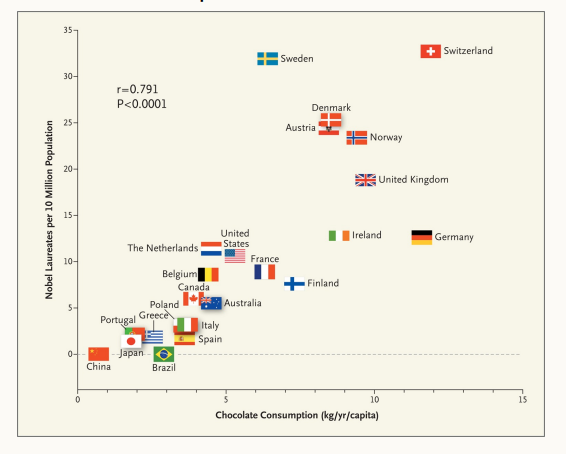
위 그림은 각 나라별 초콜렛 섭취량과 인구 10만명 당 노벨상 개수를 보여주는 Scatter Plot이다.
1단계 관측계층에서 보여지는 상관관계가 존재하며, 2단계의 정보는 존재하지 않다.
2단계의 정보가 존재하지 않기 때문에, '초콜릿을 많이 먹이면 노벨상을 많이 탈 것이다' 라고 결론 내리지 못하고, 나라가 부유해서 기초과학에도 돈을 더 투자할 수 있고, 디저트도 더 많이 먹기 때문에 나타나는 결과로 생각한다.
Simpson's Paradox
- 환자가 결석 때문에 병원에 찾아온다
- 의사가 환자를 진찰하고 처방한다.
- 처방에 따른 결과 리포트를 작성한다.
- 헬스케어 데이터로 사용한다.

위와 같은 실험 결과가 있을 때, 신장 결석의 크기에 따른 치료 약으로 A가 B보다 좋아보인다.
하지만 이때, 정말 A가 B보다 더 좋다고 말할 수 있을까?, 데이터를 합친 Treatment를 계산해보면, 아래와 같은 지표가 나타난다.
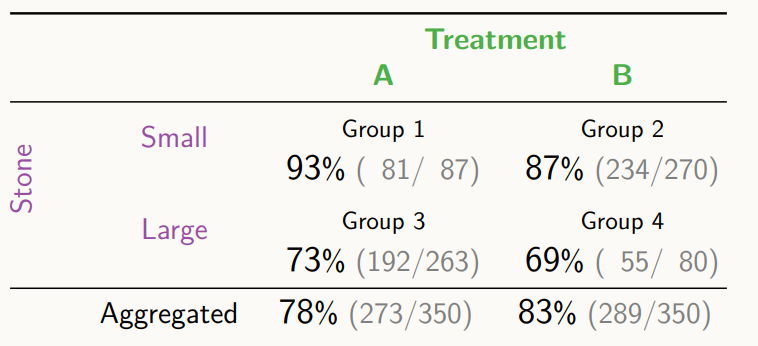
각각의 신장 결석 사이즈에 대해 비교했을 때, A가 더 좋았지만, 데이터를 통합한 경우로 비교해보면 B가 더 좋은 것처럼 나온다.
이때, 환자는 신장결석을 가지고 있고, 의사는 신장결석 정보에 따라 처방을 내린다. 결석의 상태와 처방에 따라서 환자의 나중 건강상태가 결정되는데, 처방 A와 처방 B의 효과를 알기 위해서는 처방이라는 것을 생각해봐야 한다.
환자의 상태와 무관하게 처방 A, 처방 B를 무작위로 내리는 것이기 때문에, 처방은 더 이상 신장 결석의 사이즈에 무관하다. 이 때, 가상의 무작위 실험을 생각해보면 인과 효과를 계산할 수 있다.
무작위로 처방을 내렸을 때의 건강결과는 어떻게 될 것인가?
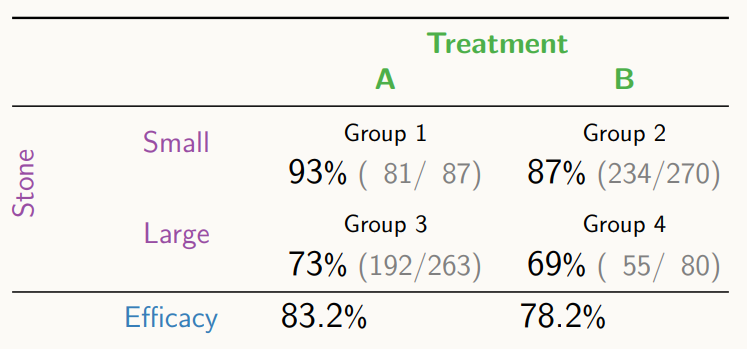
결론적으로 보아, 처방 A가 처방 B보다 좋음을 알 수 있다.
simpson's paradox를 통해 알 수 있는 개념은 다음과 같다.
-
인과적인 분석을 하기 위해서는 주어진 데이터 뿐만이 아니라, 각 변수들이 가지는 인과적 관계에 대한 자세한 이해가 필요하다.
-
주어진 데이터가 상관성을 지니고 있는지, 인과성을 지니고 있는지 고려해야한다.
-
알고자 하는 질문이 단순히 조건부 확률 같은 상관성에 관한 것인지, 인과성에 관한 것인지 고려해야한다.

일반적인 관측 연구 (observational Study)는 주어진 데이터에 대한 상관성을 그대로 설명하는데 중점을 둔다. 하지만, 자연 과학에서 이루어지는 실험이라던지, 회사에서 많이 수행하는 테스트, 인공지능에서 보는 강화학습과 같은 경우에는 Question도 casual, Data도 casual이다.
반면에, 인과추론이라고 하는 것은 앞서 설명한 1계층과 2계층을 넘나드는 추론을 말한다. 즉, 인과적인 통찰을 이용해서 하는 모든 추론을 Casual Inference라고 넓게 정의한다.

위 그림처럼 속을 알 수 없는 black box에 대해 우리는 몇몇 변수들을 관측하여 observation data를 얻을 수 있다. 만약 실험을 진행한다면, 실험 데이터를 얻을 수 있고, 가상 데이터를 얻을 수 있을 것이다.
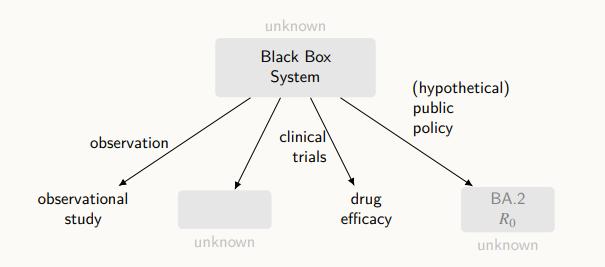
인과추론은 우리가 알 수 없는 실험 결과를 관측 데이터와 연결하는 것으로, 이 두 가지를 연결하려면 블랙박스에 대한 형식적이고 수학적인 이해가 필요하다.
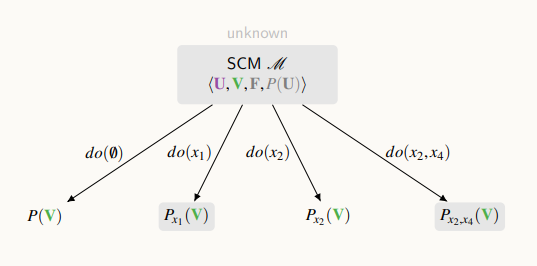
위의 그림은 시스템을 추상화한 모델이다.
모든 관측가능한 변수들의 값을 생성해내는 인과적 메커니즘을 정의한다.
이 모델을 통해서, 우리가 어떤 중재도 하지 않을 경우, P(V) 즉, 관측 가능한 모든 변수들에 대한 관측 분포를 볼 수 있는 것이고, 우리가 임의의 변수를 중재하게 될 경우에, 어떤 실험을 한다면 실험에 대한 결과 분포가 나오게 될 것이다.
x가 어떤 소문자 값으로 고정되어있을 때 변수 V는 어떻게 분포될 것인가를 설명한다.
Structural Casual Model
연구자들은 시스템은 어떨 것이다 라는 인과적인 가정을 하게 되는데, 이것은 casual diagram으로 표현될 수 있다. casual diagram은 전문가의 지식이나 상식 또는 가정에 의해서 만들어진다.
structural casual model은 4가지의 값으로 정의된다.

-
U: 관측되지 않는 변수 -
P(U): 관측되지 않는 변수에 대한 불확실성 (확률분포) -
V: 관측 가능한 변수 집합 -
F: 관측할 수 있는 각각의 변수들에 대해, 어떻게 계산되는지 정의한 함수로,V나U의subset이 들어오는데, 이 인자가 변수X를 결정하는 원인으로 생각할 수 있다.
예를 들어 설명하자면,

V : 흡연, 암에 걸린 것
U : 담배를 피게 하는 사회적 요인, 암에 걸리게 하는 환경적 요인, 사람들의 유전적인 정보
F : 흡연과 암에 대한 함수적인 특징
이러한 전문가들의 가정을 모델로 생각할 수 있고, 모델은 인자와 변수들간의 관계를 통해 다음과 같은 그래프 형식을 통해 이해한다.
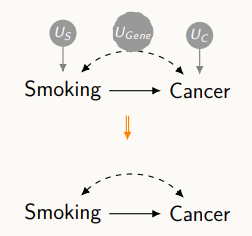
그래프에는 U 3개와 V 2개가 표현되어 있고, 이 사이에는 directed edge가 존재한다. directed edge는 결국 어떤 원인이 어떤 결과에 영향을 준다라고 해석할 수 있어, 그래프를 간략하게 파악한다면 흡연과 암사이를 directed edge로 표현할 수 있다. 또한, 그림에서와 같이 U_gene 유전적 요인은 두 변수에 영향을 줌을 알 수 있다.
인과적 연구를 위한 프레임워크가 주어져 있는데, 중재라는 것을 형식적으로 정의하자면
-
주어진 모델에서 변수
X를 중재한다고 하는 것은, 해당 변수가 원래는 함수에 의해 값이 결정되었는데, 그 값을 임의의 상수로 고정하는 것이다. 또한, 이것은 조건부확률이 아닌,do operator를 이용해서do(x)로 표현한다. -
원래 모델에서 변수
x가 고정되어 기존의 모델이 아닌 고정된 모델이 만들어진f(x)를 상수로 대체한 것을submodel이라고 표현한다.
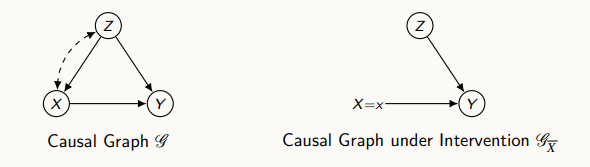
위 그림처럼, 모델의 그래프가 왼쪽과 같이 나와있을 경우 x를 상수로 고정하고 do operation을 진행한 그래프는 오른쪽 그림과 같이 생각할 수 있다.
이전에는 x에 영향을 주는 Z와 Y가 존재했는데, 두 변수가 모두 x에 영향을 미치지 않도록 중재를 했을 시에는 x로 향하는 directed edge를 삭제하여 오른쪽 그림과 같이 표현할 수 있다.
이러한 과정을 통해 인과효과를 정의하면,
임의의 변수 집합
X가 있고, 이 집합X가 고정되었을 때 우리가 관심을 가지고 보는 변수들Y가 특정 값을 가지는 확률은 어떻게 될까? 라는 것으로,P_x(y)와 같이 표현하거나P(y|do(x))로 표현한다.
다른 많은 분야에서는 기댓값을 나타내는 expectation을 사용하여 E[Y|do(x)]와 같이 나타내기도 하며, 두 가지의 다른 조치를 했을 때 y값이 어떻게 변하는지를 나타내는 difference를 사용해 차이를
E[Y|do(X=1)]-E[Y|do(X=0)]와 같이 나타내기도 한다(Average Treatment Effect, ATE).
인과추론이라는 것을 하게될 때는, 주어진 데이터가 있고, 이 데이터는 상관성만을 지니고 있고 우리는
casual diagram을 계산하기 위해서는 이에 내포되어 있는 모든 정보를 이용해서 인과효과를 계산해야 한다.
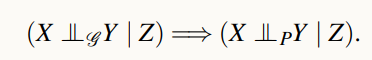
그래프에 어떤 정보가 담겨져 있고 그것을 우리가 관측 데이터로부터 인과효과를 계산할 때 제일 많이 사용하는 정보는 변수들 간의 인과관계도 있고, 인과관계를 통해 그려진 그래프에서 나타나는 조건부 독립성이라는 것이 존재한다.
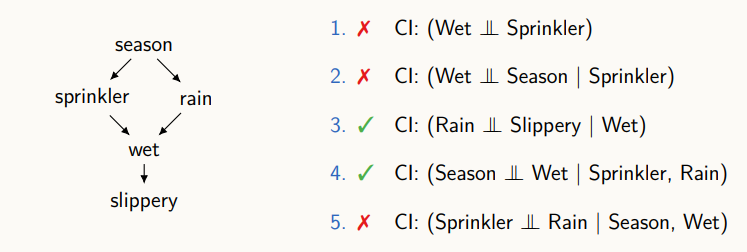
위 그래프에는 계절, 스프링클러, 비가 옴, 땅이 젖음, 땅이 미끄러움의 5가지 변수가 있고, 각 변수간 인과관계가 directed edge로 표현되어 있다.
directed edge에 대한 정보를 통해 변수 간의 조건부 독립성이 어떻게 만족되는 지를 확인할 수 있다.
그림의 우측에 나와있는 x와 체크 표시는 conditionally independent한 지를 나타내었다.
이런 식으로 그래프에서 어떤 두 변수 간의 경로가 존재하는지, 열려있는지, 닫혀있는지를 판단할 수 있는 어떤 것이 있는데 우리는 이러한 행위를 통해 조건부 독립성을 이끌어낼 수 있다.

주어진 그래프가 내포하고 있는 조건부 독립성이 있는데, 이를 컴퓨팅적으로 계산하는 것을 d-sepatation이라 칭한다. 그래프에서 조건부 독립성을 읽어낼 수 있는 알고리즘을 뜻한다.