해당 시리즈는 LG에서 지원하는 LG Aimers의 교육 내용을 정리한 것으로, 모든 출처는 https://www.lgaimers.ai/ 입니다.
Casual Effect Identifiability
이번 장에서는 인과효과를 계산하는 방법에 대해 알아본다.
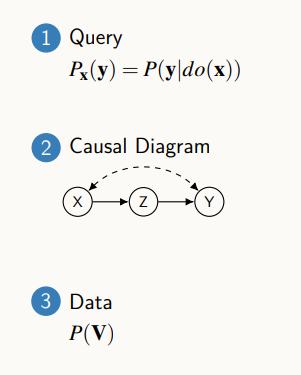
위의 3가지를 이용하여 인과추론 알고리즘을 통해 계산을 진행한다.
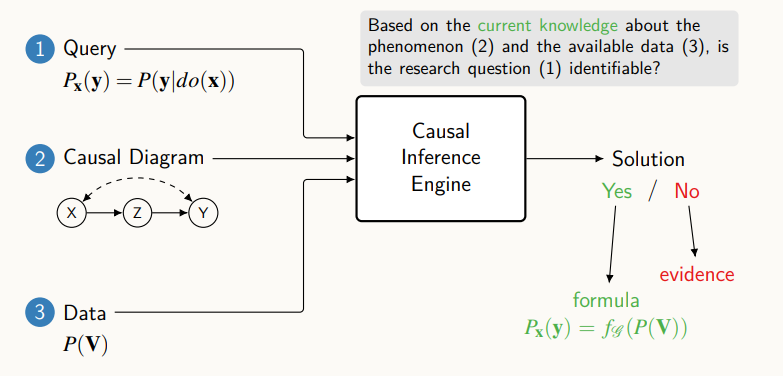
계산이라고 말은 했지만, 특정할 수 있는지를 물어보는 것이고, 실제로 가능하다면 인과효과를 계산할 수 있을 것이고, 특정할 수 없다면 계산할 수 없다는 것이 아니라, 주어진 그래프와 데이터가 있을 때 그래프에 호환이 되는 2가지의 다른 모델에서 정의되고 있는 인과효과가 달라 이 값은 특정할 수 없다라고 판단한다.
예를 들어 인과효과를 계산한다.
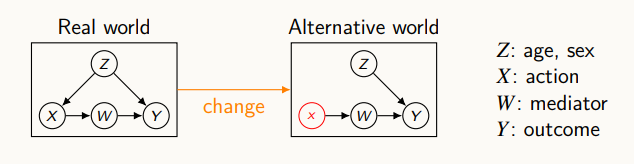
왼쪽에는 주어진 그래프에는 Z, X, W, Y 변수가 있고 X에 중재를 하려고 할 때, Z 변수는 X와 Y에 서로 영향을 미치는 교란 변수이며, W 변수는 X와 Y 중간에 있는 변수 (mediator)이다.
이 때 가상의 중재를 생각해보면, 오른쪽 그림과 같이 설명할 수 있다. X는 더이상 Z의 영향을 받지 않기 때문에, Z에서 X로 향하는 edge를 지우고, X는 고정이 되어있기 때문에 x로 표현한다.
여기서 얻어지는 질문은, 데이터가 생성되면 Y는 어떤 식으로 분포될까? 하는 것이다.
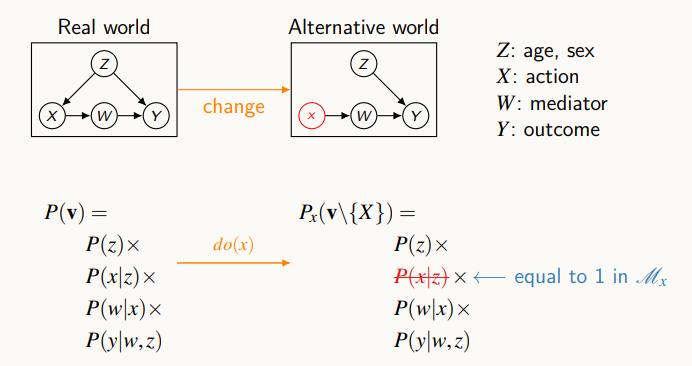
주어져 있는 V에 있는 모든 변수에 대해 P(v|pa(v))의 조건부 확률들을 곱하면 결합확률을 계산할 수 있다. 중재를 했을 때의 확률을 보면, X가 중재되었기 때문에 X는 더 이상 Z에 대해 분포되어 있는게 아닌, 중재된 값 x로 고정되어 있기 때문에, P(x|z)는 1로 변하는 것을 생각해볼 수 있다.
결합 확률을 식으로 decompose 해놓고, 거기에 x가 나오는 확률을 1로 바꾸면 중재 때의 확률분포를 예상할 수 있다.
Computing Casual Effects from Observational Data
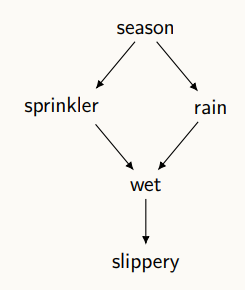
주어진 결합 확률 P(V)는 다음과 같이 나타낼 수 있다.
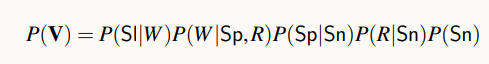
이 상황에서 스프링클러에 중재를 한다는 것은 스프링클러를 킨다는 뜻이고, 이럴 경우에 땅은 얼마나 젖을 것인가, 라는 것을 알고 싶을 때에는 결합확률과 주변확률의 정리를 이용해 식을 전개할 수 있다.

지금까지는 식을 전개 해놓고, 결합 분포에서부터 중재하고 있는 변수와 관련된 조건부 확률을 제거 해서 인과 효과를 계산했다. 하지만, 이런 방법을 사용하기 위해서는 그래프의 모든 변수들이 모두 관측 가능해야한다.

인과 효과 P(y|do(x))는 위의 식처럼 계산할 수 있다. y, x, pr(x)가 주어졌을 때 결합확률을 전개한 후, x|pa(x)를 제거한 꼴이라고 생각할 수 있다.
지금까지 설명한 방식은 모든 변수들이 모두 관측가능한 경우에 사용할 수 있는 방법이다.
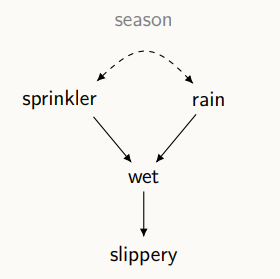
위 그림은 season이 관측되지 않았을 경우의 그림을 나타낸다. 이 상황에서 sprinkler에 중재를 가한다면, 식은 다음과 같이 전개된다.
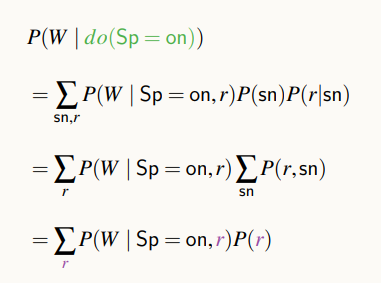
이런 식으로, 인과효과를 구하려고 할 때 보이는 식을 Adjustment Formular라고 표현한다.
예를 들어, 위의 식은 r-rain 이라고 adjust한 식을 말한다.
Back-door Criterion
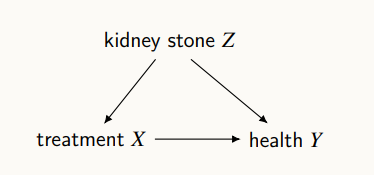
X가Y에 직접적으로 연결되어 있기 때문에 나타나는 인과적인 상관성Z에 따라서X가 영향을 받고,Y가 결정되기 때문에,X와Y가 직접적인 관계가 없더라도, 교란변수에 의해 나타나는 상관성
여기서 인과 효과를 고려한다는 것은, X가 변하면 Y가 어떻게 변할까, 라는 생각을 하는 것으로, 데이터에 나타나는 상관성에서 교란에 의한 상관성을 제거하고자 하는 것이다.
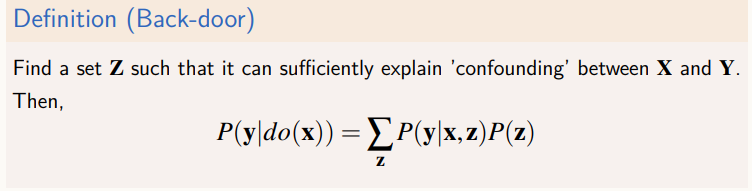
Z를 찾으면 adjustment formula를 이용하여 우리가 원하는 인과효과를 계산할 수 있을 것이다.

Z는X이후에 나타나면 안된다.Z라는 것은,X에서Y로 가는 길목들 중, 뒤로 가는 길목들을 모두 막을 수 있어야 한다.
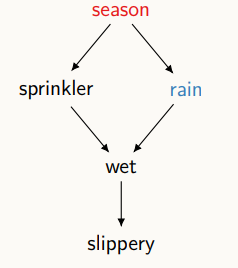
스프링클러에 대해 wet이 어떻게 바뀔 것인가에 대해 인과효과를 계산하고 싶으면, 뒷문이라고 생각할 수 있는 선은 sprinkler - season - rain 경로다. 그렇기에, 본 그림에서 Z에 해당하는 것은 season, rain, {season, rain}이다.
예를 들어 확인해보면,
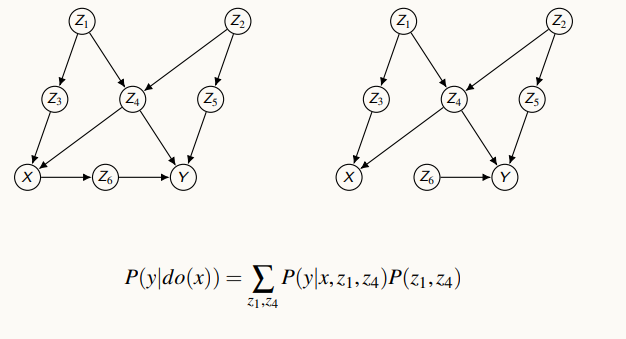
X와 Y가 아래 있고, 다른 여러가지 변수가 존재한다. 이때, X와 Y의 뒷문을 막는 변수 Z를 찾아낼 것인데, 이때 Z6는 X의 뒤에 있으므로 제외한다.
Z4를 통한 뒷문Z1을 통한 뒷문Z2를 통한 뒷문
3가지 뒷문을 모두 막을 수 있는 집합 Z를 찾는게 목적이다.
Z = {Z4, Z1, Z2}
뒷문 조건을 만족하는 변수들을 찾기 위해서는 X의 decendent를 고려하지 않기 때문에, 뒷문만을 고려하는 방법으로 주어진 그래프에서 X에서 나가는 길, edge를 제거한 오른쪽과 같은 그래프를 이용해 조건부 독립되는 변수 Z를 찾으면 된다.
"back-door criterion은 sound 하다" 라고 표현하는데, 이것을 통해서 우리가 어떤 formular를 찾을 수 있지만, 모든 formular는 찾을 수 있는 것을 보장하지 않는다. 이러한 문제점을 해결하는 방법이 Do-calculus다.
Do-calculus
do-calculus는 여러가지 다른 중재 조건에서 나오는 확률들끼리 서로 연결고리를 만들어주고 서로 다른 중재로 어떤 확률 분포를 바꿔주는 역할을 뜻한다.

do-calculus는 위의 3가지 규칙으로 구성된다.
-
관찰에 대한 것이 추가되거나 삭제될 수 있다. = "조건부 독립"
-
Action과Observation을 바꿀 수 있다. =x로 들어가는edge를 지우고Z에 대해서는 나가는edge를 지운 그래프에서 조건부 독립을d-seperation을 통해 확인하면 적용 가능하다. -
Action이 추가되거나 제거될 수 있다. = 확률을 계산함에 있어서,Action을 취하는 것이 아무런 영향을 미치지 못한다.X와Z가 동시에do된 상황에서Z가Y와 조건부 독립일 때 적용 가능하다.
어떤 규칙에 의해 조건부 독립을 만족하는 것을 찾으면, 확률을 다른 확률로 변경시킬 수 있다.
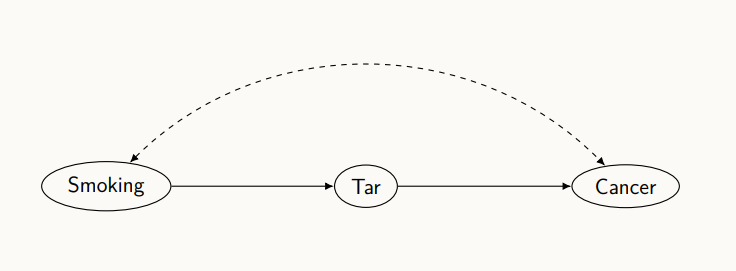
흡연 - 암 사이에 타르라는 새로운 변수가 있다. 흡연과 암은 directed edge이 존재하지 않아, 흡연은 암걸리는데 직접적인 영향을 미치지 않고, 타르에 의해 걸리는 것이다. 라는 가정을 세우고 그린 그림이다.
위 그림에는 back-door 방법이 적용되지 않는다. 흡연이 암에 미치는 영향을 알려고 할 때, back-door를 막아줘야 하는데, 막을 수 있는 변수가 존재하지 않는다.
이때, do-calculus를 이용해 인과효과를 계산하면 다음과 같이 전개가 가능하다.

back-door 같은 경우 sound하지만 complete하지 않고, do-calculus 같은 경우 sound하고, complete하다고 한다. 모든 Identifiable한 formular에 대해서 인과효과를 계산하는 식은 do-calculus와 공리를 이용해 이끌어낼 수 있다.
하지만, 어떤 룰들을 어떤 식으로 적용해야, 우리가 원하는 식에 도달할 수 없다. 다행스럽게도, 최근에는 알고리즘의 개발로 효과적으로 인과효과가 계산될 수 있는지 없는지를 판단한 후, 가능하다면 인과효과를 계산하는 식을 이끌어낸다.