해당 시리즈는 LG에서 지원하는 LG Aimers의 교육 내용을 정리한 것으로, 모든 출처는 https://www.lgaimers.ai/ 입니다.
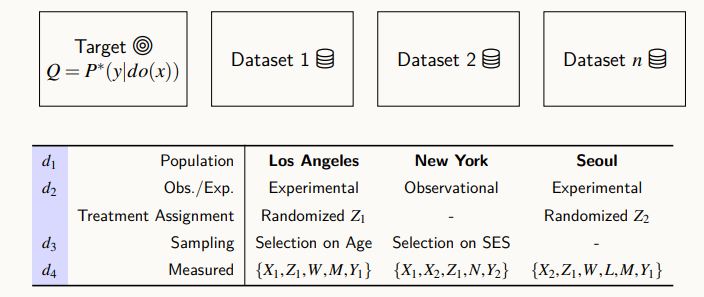
위의 3 도시는 서로 다른 데이터를 만들어낸다. LA는 Z1에 대한 실험을, 뉴욕은 간단한 관찰을, 서울은 Z2에 대한 실험을 진행했다.
LA의 데이터셋은 데이터를 샘플링하는데 있어, 인구 모집단에 대해 무작위 샘플링을 한 것이 아니라, 특정한 변수인 나이에 대해 샘플링을 진행했다.
뉴욕의 경우, Socioeconomic Status, SES라고 하는 사회 경제적인 사람들의 상태에 따라서 데이터가 수집될 수 있는 특징을 이용했다.
이런 식으로 데이터는 다양한 특성을 가지고, 인과 추론을 하는 데 있어 이러한 특성들을 고려하지 않고, 인과 추론 방법론을 이용해서 데이터를 활용하려고 한다면, 편향이 있는 값이 계산될 수도 있다.
Generalized Identifiability
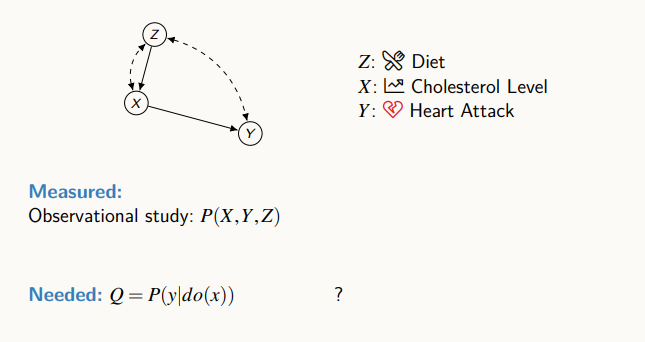
위 그림에서 Z는 식이요법, X는 식이요법에 영향을 받는 혈 중 콜레스테롤 수치, Y는 심근경색일 때, 콜레스테롤이 심장에 주는 영향을 계산해보려한다.
Z를 통하는 back-door를 막을 수 있을 것 같지만, Z-Y의 연결 때문에 사용할 수 없다.
인간은 기술적으로 몸 안에 있는 콜레스테롤 양을 마음대로 바꿀 수는 없다. 하지만, 식습관을 조절해서 실험을 진행할 수 있다. 실험 데이터가 있다고 가정한 경우, 아래와 같이 계산할 수 있다.

do-calculus와 실험 데이터를 이용해 계산할 수 있다.
Drug-Drug Interactions
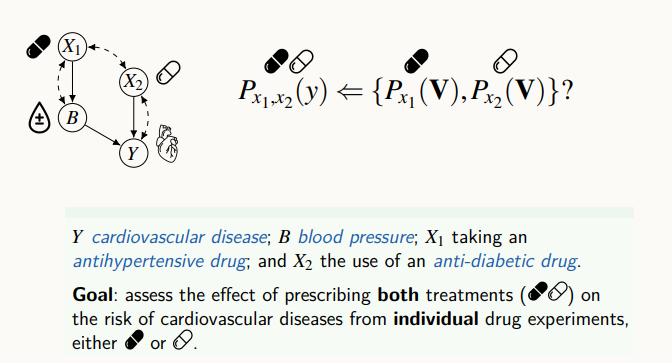
x1, x2는 각각 다른 약으로, x1은 혈압약 x2는 당뇨병약일 때, B는 혈압 정보, Y는 심장병을 뜻한다.
약 2개를 동시에 복용을 했을 때, 심장이 어떻게 반응할까? 라는 의문에 대해 존재하는 실험 데이터는 x1 약에 의해 실험된 데이터, x2에 대해 실험된 데이터가 있다. 각각의 약에 대한 실험 데이터가 존재할 때, 두 약을 혼용 했을 때 어떤 결과가 나올 지를 알고싶은 문제다.
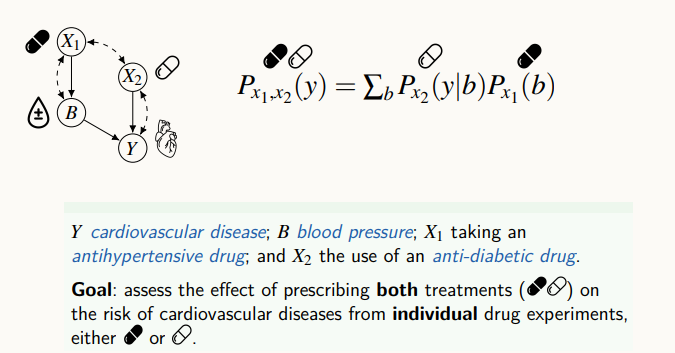
각각의 실험데이터로부터, 조건부 확률과 marginal distribution을 이용해 인과 효과 계산 식을 도출할 수 있다.
주어져 있는 인과 효과가 있을 때, 알고리즘을 통하면 마치 devide & conquer 방식과 같이 인과 효과를 더 작은 인과 효과를 계산하는 문제로 쪼갠다.

만약 Z에 대한 실험 데이터가 존재한다면, 각각의 factor 들은 do-calcuclus를 이용해 원하는 식을 계산할 수 있다.

즉, 여러가지의 데이터를 활용하는 General Identifiability도 결국 do-calculus가 있으면 우리가 원하는 인과효과를 계산할 수 있다. general identifiability는 여러 데이터가 한 도메인에 주어져 있을 때, 그것을 활용해서 원하는 인과 효과를 계산하는 과정을 뜻한다.
기계학습에서 학습 데이터셋과 테스트 데이터셋이 같은 환경에서 만들어져 distribution shift라는 게 일어나지 않아, 학습 데이터셋으로 학습을 진행하고 테스트셋에 그대로 적용 가능할 것이라고 가정한다.
Transportability는 주어져 있는 데이터의 소스와 우리가 인과 효과를 계산하고자 하는 타겟이 서로 다른 도메인일 때의 인과 추론을 다룬다. 이러한 문제는 단순한 인과 추론이 아닌, 통계적 추론에 해당하는 문제다. 일반적인 추론에서 우리가 일반화를 어떻게 할 것인가에 대한 문제다.
Transportability: the Spectrum
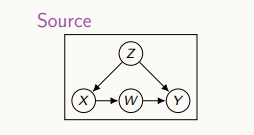
위 그림에서 source는 실험이 이루어지고 있는 환경을 뜻한다.
첫 번째 가정으로, "만약 source와 target이 모두 같다면, 우리가 실험실에서 나온 결과를 우리가 원하는 타겟에 그대로 적용할 수 있을 것이다.
두 번째 가정으로, "만약 source와 target이 모든 다르다면, 우리가 실험실에서 나온 결과를 우리가 원하는 타겟에 그대로 적용할 수 없을 것이다.
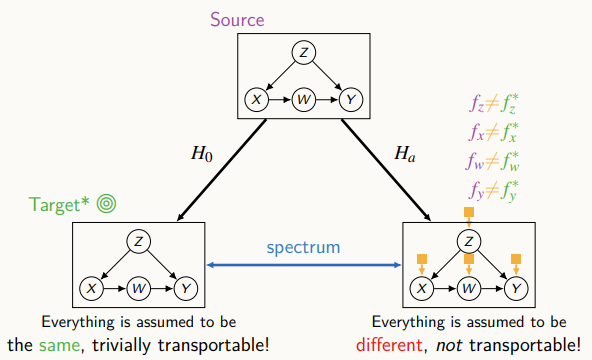
위 그림에서 왼쪽 아래는 첫 번째 가정의 경우를 나타내고, 오른쪽 아래는 두 번째 가정의 경우를 나타낸다.
조금 더 현실적인 가정은 첫 번째 가정과 두 번째 가정 사이에 어딘가를 고려하는 것이다. 즉, soruce와 target의 어떤 공통점이 존재하지만 부분적으로 어떤 변수에 대해서는 다를 수 있다.
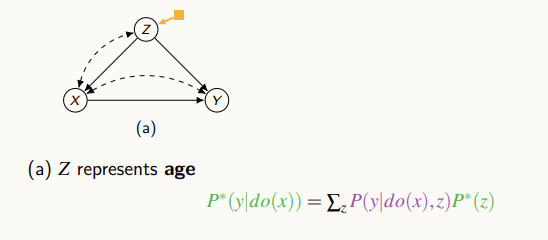
위 그림에서 노란색 노드는 switch의 개념으로 이해한다. source와 target을 하나의 그래프로 표현한 것이다.
만약 노란 노드가 source라고 하면, f_z는 f_source, f_target에 따라 맞는 메커니즘을 수행한다. 위의 그림을 해석하면, source에 실험 데이터가 있고, 이를 통해 target의 인과효과를 계산하려고 하는데 Z라는 변수에 차이점이 있다는 것이다.
Z가 주어져 있고, x에 중재되어있는 경우 target은 영향을 주지 않기 때문에, source로 바꿀 수 있다. 즉, source에서의 조건부 확률과 target에서의 확률을 결합하여 인과 효과를 구한다.
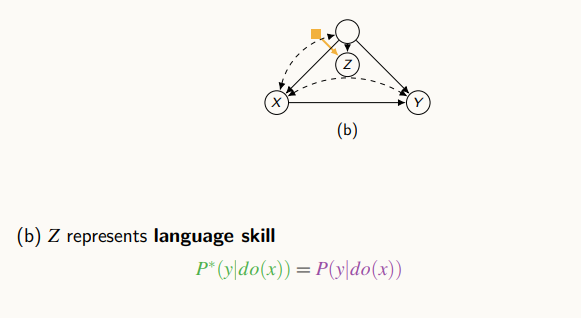
위 그림은 X와 Y가 존재하고, 교란 변수에 차이점이 있는 게 아니라, 교란 변수의 차일드에 차이점이 있는 경우다. 이럴 경우 Z라는 변수가 주어져 있지 않으면, Y나 다른 변수에 영향을 주지 않기 때문에,
d-seperation을 쉽게 적용하여 인과 효과는 source와 target 두 도메인에 대해 같음을 알 수 있다. 그로 인해, source의 인과 효과를 그대로 사용한다.
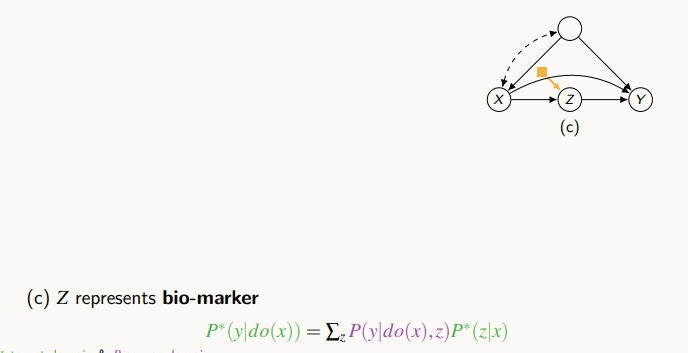
위 그림은 X와 Y사이의 변수 즉 mediator인 Z에 차이점이 있을 때다.
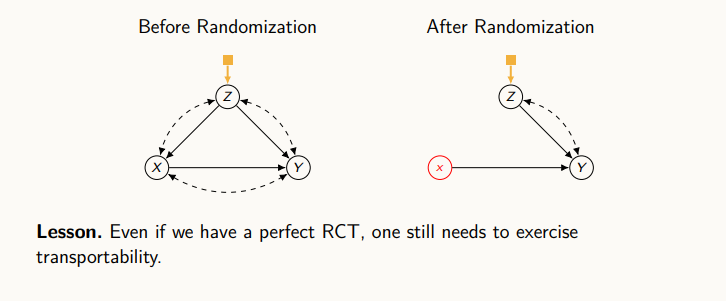
우리가 보통 무작위 실험을 통해 실험 데이터를 얻는데, 실험 데이터의 결과를 우리가 절대적으로 받아들이는 경우가 많다. 하지만, 실험이 일어난 모집단과 인과 효과를 적용하고자 하는 다른 집단 간의 차이가 존재한다면 실험 데이터의 인과 효과를 우리가 원하는 타겟에 사용할 수 없다. 그렇기에, 실험데이터를 활용하고자 한다면, 이런 Transportability라는 개념을 통해서 casual diagram을 그리고, 어떤 변수들이 다른지를 명시화하고 알고리즘을 통해 문제를 푸는 개념이 필요하다.
transportability 알고리즘 역시 do-calculus를 기반으로 하고 있고, sound하며 complete하다.
데이터의 샘플링 과정에서 선택 편향이 생긴 경우
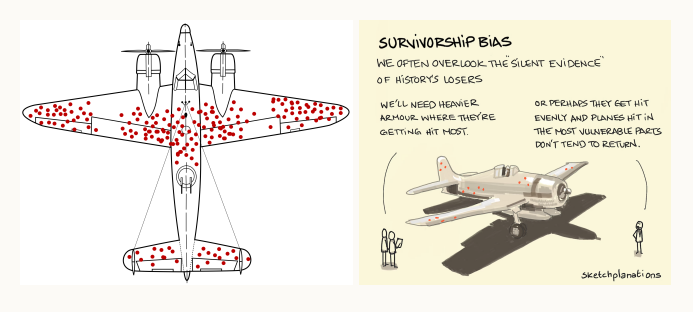
위 그림은 전투기가 전쟁에서 총에 맞은 위치들을 나타낸다. 만약 위 사진을 보고, 저런 부분에 총을 많이 맞으니 빨간 점이 많은 부분을 강화하고자 하는 행위는 올바르지 않다. 조종석이나 엔진에 총을 맞은 경우 돌아오지 못해 데이터를 수집하지 못한 것이다.
위와 같이 데이터의 샘플이 선택적으로 포함되는 경우에 발생되는 편향을 선택 편향 (Selection Bias) 라고 한다.
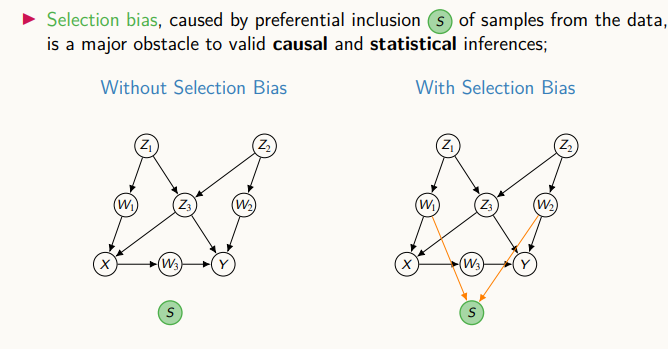
위 그림은, 기존 casual diagram에 새로운 변수 S를 추가한 것이다. S라는 것은 샘플이 데이터에 포함되었는지, 되어있지 않은지를 표현하는 변수다. 만약 S가 1이면 포함, 0이면 미포함이다. 이는 샘플이 데이터에 포함될지 안될지는 무작위로 선택된다. 오른쪽 그림은 selection 변수가 있을 때의 그림을 나타낸다. S가 W1, W2에 영향을 받는다.
왼쪽 그림의 경우는 P(V|S=1) = P(V), 오른쪽 그림의 경우 P(V|S=1) != P(V)다.
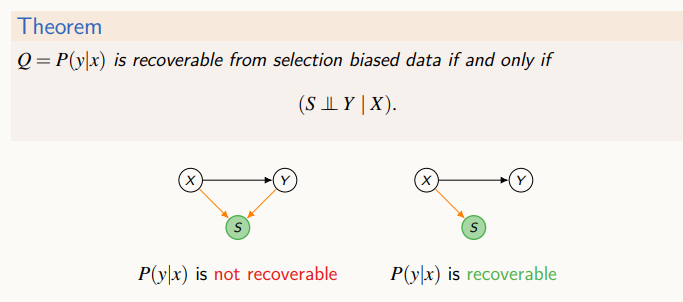
selection 변수 s가 X와 Y가 주어졌을 때 독립적이면 P(y|x)를 계산할 수 있다.
P(x,y|s=1) => P(y|x, s=1) = P(y|x) 편향이 없을 때의 조건부 확률과 편향이 있는 데이터 안에서의 조건부 확률이 같다고 결론을 내릴 수 있다. 하지만, 위의 Theorem을 만족하지 않는 경우가 대부분이다.
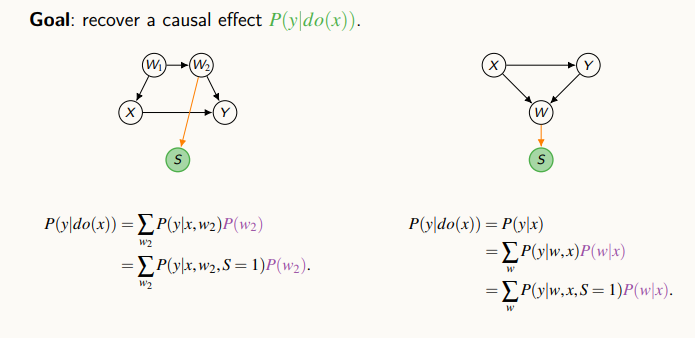
왼쪽 그림에서는 X와 Y가 있고, 뒷문을 통해 W1, W2가 연결되어 있고, W2가 S에 영향을 주고 있다. 이때, back-door를 이용해 식을 전개했고, W2가 주어져 있는 상황에서 S 변수는 다른 변수에 영향을 주지 않기에, 최종 식을 도출할 수 있다.
오른쪽 그림에서는 do-calculus와 조건부확률을 이용해 인과 효과를 계산할 수 있다.
selection bias 문제를 푸는 데 있어서 nonparametric, 어떤 함수적 가정이 없고, 외부 데이터가 없는 경우에는 다항시간에 문제를 효율적으로 푸는 알고리즘이 존재한다.
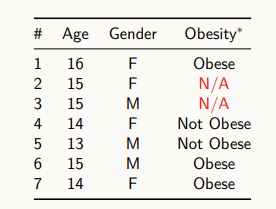
위 테이블에서는 나이, 성별, 비만도가 표현되어있다. N/A는 데이터가 주어져 있지 않은 누락된 경우다.
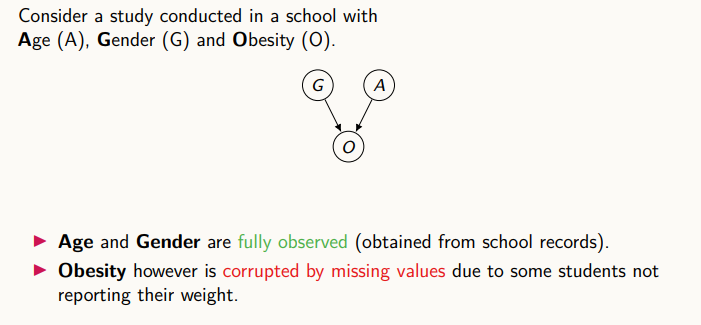
나이, 성별, 비만도는 위와 같은 casual diagram으로 표현할 수 있다. G와 A에 대한 정보는 학교나 기타 기관에 정리되어 있어누락될 수 없지만, O의 데이터는 설문조사를 통해 수집한다고 했을 때, 누락될 수 있다.
누락된 변수 O에 대해 서로 다른 변수 2개를 생각한다.
- 실제 학생의 비만도
- 비만도가 누락되는 메커니즘

O^*는 실제 리포트 된 비만도를 나타낸다. 오른쪽에 보이는 식과 같이 생각할 수 있다.
다음은 누락된 데이터가 만들어지는 과정을 나타낸다.
-
데이터가 누락되지 않는 경우
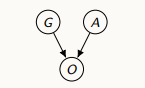
-
비만도가 누락되는 원인이 랜덤한 경우 (무작위로 데이터가 누락되는 경우)
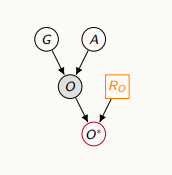
-
나이에 의해서 누락이 되는 경우 (학생들이 사춘기라 설문조사를 안할 경우)
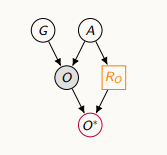
-실제 비만도 값에 의해 누락되는 메커니즘이 영향을 받는 경우 (몸무게를 드러내고 싶지 않은 경우)
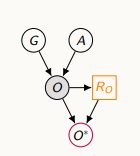
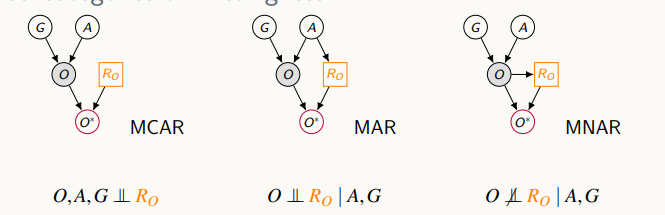
누락의 원인을 3가지로 분류한다.
Missing Completely At Random (MCAR)- 완전 무작위Missing at Random (MAR)- 매커니즘이 누락된 변수와 어떤 조건부 독립이 성립Missing Not at Random (MNAR)- 랜덤하지 않은 누락
일반적으로 누락된 정보가 있으면, 해당 줄들을 삭제하고 빈 값들을 채워 넣는다. MCAR이나 MAR에 부분적으로 동작하지만, MNAR에는 동작하지 않는다.
명시적인 이해 없이는, 누락된 데이터로부터 원하는 값을 정확하게 구해낼 수 없고, 결과에는 편향이 생길 수 밖에 없다.

첫 번째 term은 편향된 데이터로부터 구할 수 있는 조건부 확률이며, 두 번째 term은 누락된 데이터로부터 A만 활용한다.
지금까지의 과정은 누락된 데이터로부터, 누락되지 않은, 편향되지 않은 상태에서의 결합 확률을 구하는 것을 causal diagram의 누락 메커니즘을 활용해서 문제를 풀었다.
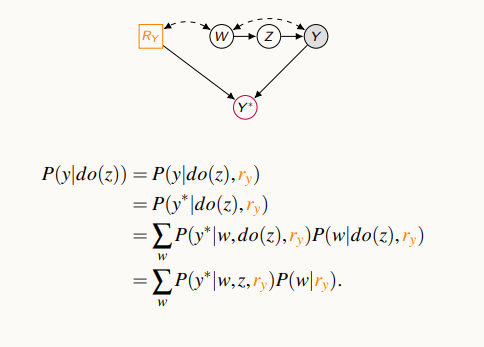
식의 형태를 보면, 편향된 데이터에서 back-door adjustment를 수행함을 알 수 있다.
데이터가 만들어지는 인과 과정을 이해, 도메인이 어떻게 다른지 표현.

인과성 연구 분야
- 인과성을 활용한 데이터 융합
casual data science - 데이터로부터 정보를 이용해 인과 관계를 알아내는
casual discovery - 의사결정에 사용하는
casual decision casuality+machine learning