자료구조 & 알고리즘 면접질문 정리

Hyun·2023년 12월 19일
면접질문
0

면접질문 정리

목록 보기
1/6

https://github.com/VSFe/Tech-Interview/blob/main/01-DATA_STRUCTURE_ALGORITHM.md 의 면접질문들에 대한 답을 나름대로 정리한 포스팅


시간복잡도와 공간복잡도

  • 시간 복잡도

    • 특정 알고리즘에 대한 실행 시간을 정확한 시간으로 측정하는 것은 같은 알고리즘이더라도 언어나 실행 환경에 따라 다른 결과를 반환할 수 있다.

    • 그래서 실행 시간을 정확한 시간으로 재지 않고, 코드 라인의 실행 횟수를 가지고 알고리즘에 대한 성능을 측정한다.

    • 이때, 입력값의 길이를 n 과 같은 변수로 두고 n의 값을 매우 크다고 가정하면, 실행 횟수 수식에서 n의 최고차항만 의미있고, 최고차항의 계수나 최고차항이 아닌 값들은 의미가 없어진다.

      • 이를 점근적 분석이라 한다.

      • 의미가 없는 값들은 표기하지 않고, 의미있는 값만 간단하게 표기하는 것을 점근적 표기법이라 한다.

    • 이러한 점근적 분석을 통해, 함수의 실행 시간을 단순하게 점근적 표기법으로 표현한 것이 바로 시간 복잡도이다.

  • 공간 복잡도

    • 입력 크기에 대해 어떤 알고리즘이 실행되는데 필요한 메모리 공간의 양

    • 시간 복잡도와 마찬 가지로, 입력값의 길이를 n 이라 가정하고 점근적 분석을 통해 점근적 표기법으로 표현한다.


Big-O, Big-Theta, Big-Omega

  • Big-O

    • 알고리즘의 실행 시간이 아무리 오래 걸려도 특정 시간복잡도 이하로 처리된다를 표현하기 위해 사용되는 특정 시간복잡도

    • 즉, 알고리즘 수행시간의 상한선을 나타내며, worst case 의 시간 복잡도를 의미한다.

  • Big-Omega

    • 알고리즘의 실행 시간이 아무리 빨라도 특정 시간복잡도 이상으로 처리된다를 표현하기 위해 사용되는 특정 시간복잡도

    • 즉, 알고리즘 수행시간의 하한선을 나타내며, best case 의 시간 복잡도를 의미한다.

  • Big-Theta

    • 특정 케이스에 대하여, Big-O 와 Big-Omega 값이 같을 때의 시간 복잡도를 의미한다.

    • 즉, 상한선과 하한선이 같은 tight bound 을 의미한다.


Big-O를 사용하는 이유

  • 일반적으로 성능을 분석할 땐 최악의 경우에만 관심이 있다.

    • 주어진 입력에 대해 예상보다 빠르게 실행되는 것은, 성능 측정에서 무시할 수 있는 정보이다.

    • 그러나 주어진 입력에 대해 예상보다 느리게 실행되는 것은, 성능 측정에서 중요한 부분이다.

  • 또한 Big-Theta 의 경우 계산하기 어려운 경우가 많다.


O(1) 은 O(N) 보다 항상 빠른가?

  • Big-O 표기법은 계수, 상수를 생략한다.

    • 따라서, 아주 정확한 실행 횟수를 나타내지는 않는다.

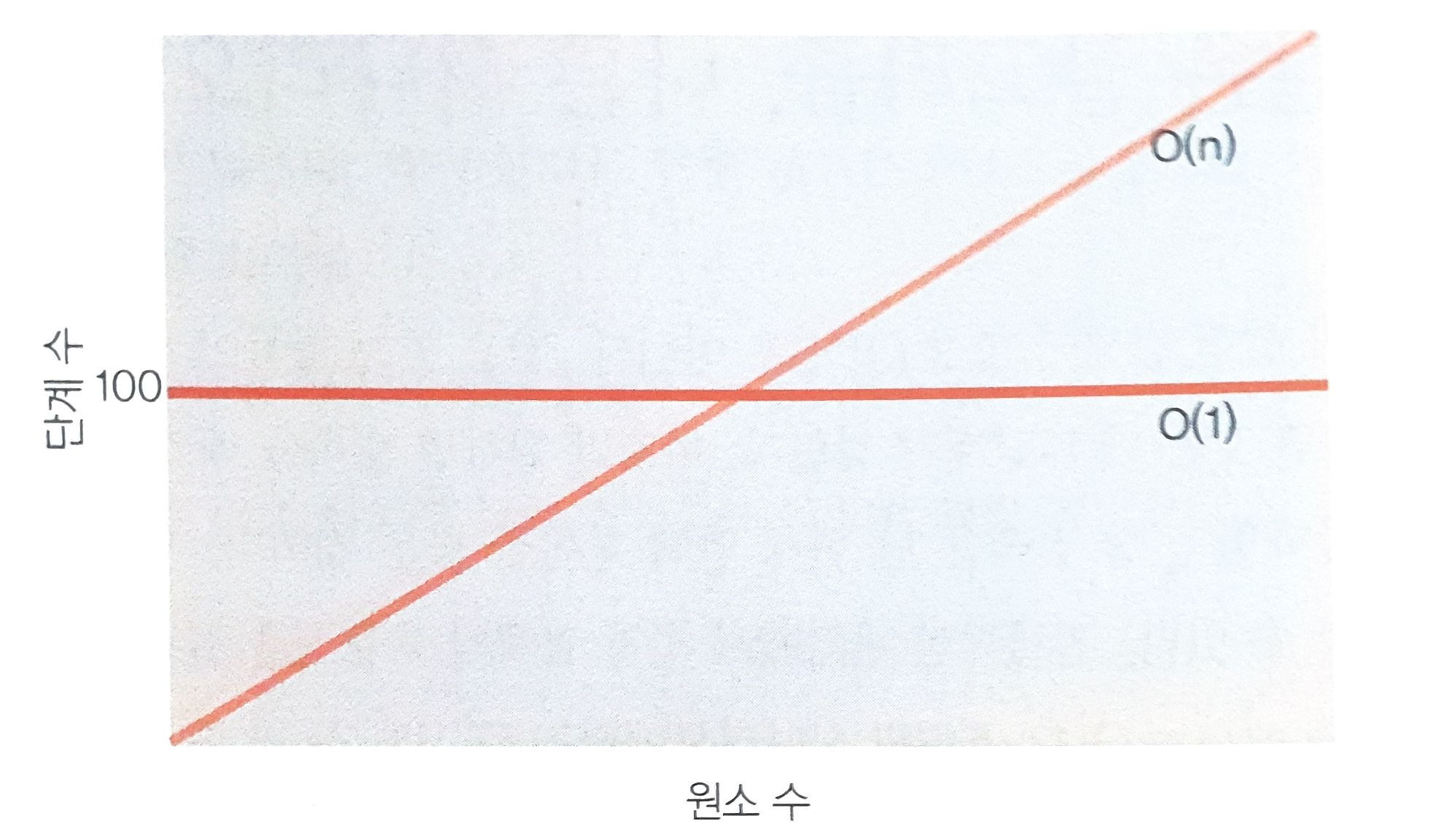
  • 만약 O(1) 의 방식이 입력값의 길이와 상관없이 기본적으로 100번의 실행 순서가 필요하고,

  • O(n) 의 방식이 입력값의 길이만큼 n 번의 실행 순서가 필요하다고 하면

  • 입력값의 길이 n < 100 인 지점에서는 O(n) 의 실행 순서가 더 적어 빠르다고 할 수 있다.

  • 따라서 시간 복잡도는 점근적 표기법이기 때문에 입력값이 무한히 큰 경우에는 O(1) 이 O(N) 보다 항상 빠르다고 할 수 있지만

  • 입력값의 길이와 상관없이 무조건 O(1) 이 O(N) 보다 항상 빠르다고 말하기에는 무리가 있다.


링크드 리스트

  • 데이터 요소의 선형 집합

  • 데이터의 순서가 메모리에 물리적인 순서대로 저장되지 않는다.

  • 특정 인덱스에 접근하기 위해서는 전체를 순서대로 읽어야 한다.

    • 이 경우 O(n) 시간 복잡도를 갖는다.

  • 탐색 시간을 고려하지 않고, 특정 지점에서 데이터를 추가하거나 삭제, 추출하는 경우엔 O(1) 시간 복잡도를 갖는다.


배열 vs 링크드 리스트

  • 배열 (정적 배열)

    • 메모리에서 물리적인 순서대로 저장된다.

      • 즉, 논리적인 순서와 물리적인 순서가 일치한다.

    • 인덱스를 바탕으로 어느 위치에나 O(1) 에 조회 가능하다.

    • 동적 배열이 아니라면, 처음부터 일정 크기의 연속된 공간을 예약해야 한다.

      • 자료 구조의 크기가 고정적이다.

  • 링크드 리스트

    • 메모리에 물리적인 순서대로 저장되지 않는다.

      • 논리적인 순서대로 저장되나, 메모리에서 물리적으로 연속된 위치에 있지는 않다.

    • 특정 인덱스에 접근하기 위해서는 처음부터 순서대로 읽어야 한다.

    • 처음부터 일정 크기의 공간을 할당할 필요 없다.

      • 자료 구조의 크기가 자유롭게 커지고 작아진다.

    • next 포인터가 위치할 메모리 공간이 추가적으로 필요하다.


링크드 리스트를 사용해서 구현할 수 있는 자료 구조

  • Stack

    • Head 바로 뒤에 값을 집어넣고, Head 바로 뒤에 값을 빼는 방식으로 LIFO 구현

  • Queue

    • Rear 포인터의 뒤에 값을 집어넣고 Rear 포인터를 뒤로 이동시키고 (enque)

    • Front 포인터의 값을 빼고 Front 포인터를 뒤로 움직이는 (deque) 방식으로 FIFO 구현

  • Deque

    • 이중 연결 리스트를 사용한다.

    • Front 포인터의 앞에 값을 추가하고, Front 포인터를 앞으로 이동시키거나 (add Front)

    • Front 포인터의 값을 빼고, Front 포인터를 뒤로 이동시키거나 (remove Front)

    • Rear 포인터의 뒤에 값을 추가하고, Rear 포인터를 뒤로 이동시키거나 (add Rear)

    • Rear 포인터의 값을 빼고, Rear 포인터를 앞으로 이동시키는 (remove Rear) 방식으로 구현

  • 해시 테이블의 chaining

    • 해시 충돌이 발생한 경우, 이미 점유된 해시 버킷에 자료를 추가하는 방식

    • 이때 자료를 추가하는 방식으로 연결 리스트를 사용할 수 있다.

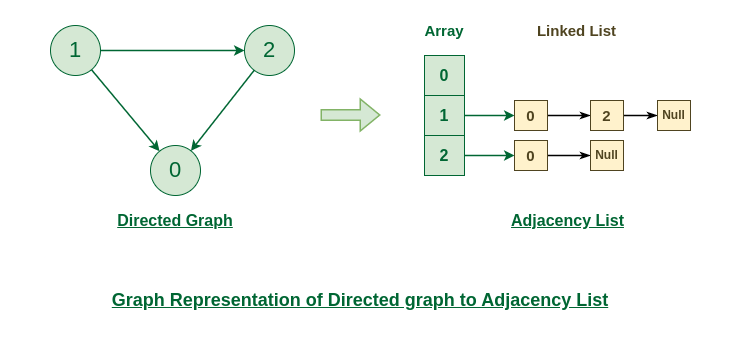
  • 그래프를 표현하는 Adjacency List

    • 그래프를 인접 리스트로 표현할 수 있다.

    • 그래프의 각 정점은 링크드 리스트로 연결된다.


스택과 큐

  • 스택

    • LIFO 자료구조

    • 데이터를 집어넣는 push 연산과

    • 가장 최근에 집어넣은 데이터를 꺼내는 pop 연산이 대표적인 연산이다. (시간 복잡도 O(1))

  • 큐

    • FIFO 자료구조

    • 일반적으로 앞을 가리키는 front, 뒤를 가리키는 rear 두 포인터를 갖는다.

    • 데이터를 넣을 땐, rear 포인터가 가리키는 뒤쪽으로 넣고

    • 데이터를 꺼낼 땐, front 포인터가 가리키는 앞쪽에서 뺀다. (시간 복잡도 O(1))

스택과 큐는 자료형의 연산만 정의하고, 자세한 구현은 정의하지 않은 추상 자료형이다.


스택 2개로 큐를, 큐 2개로 스택을 만드는 방법

  • 스택 2개로 큐 만들기
class MyQueue:

    def __init__(self):
        self.main = []
        self.tmp = []
        

    def push(self, x: int) -> None:
        self.tmp.append(x)

    def pop(self) -> int:
        
        if not self.main:
            while self.tmp:
                self.main.append(self.tmp.pop())
        
        return self.main.pop()
            

    def peek(self) -> int:
        if not self.main:
            while self.tmp:
                self.main.append(self.tmp.pop())
        
        return self.main[-1]
        
    def empty(self) -> bool:
        return (not self.main and not self.tmp)
  • offer (put)
    • tmp 스택에 새로운 값을 추가한다.
    • 시간 복잡도 O(1)

  • poll (get)
    • main 스택에 값이 없으면, tmp 스택에 있는 모든 값들을 꺼내 main 스택으로 옮긴다.
    • main 스택에 있는 값을 꺼내 반환한다.
    • tmp 큐에 있는 모든 값들을 옮기는 시간 이 필요하므로 총 시간 복잡도는 O(N)

  • 큐 2개로 스택 만들기
class MyStack:

    def __init__(self):
        self.main = collections.deque()
        self.tmp = collections.deque()

    def push(self, x: int) -> None:
        while self.main:
            self.tmp.append(self.main.popleft())
        self.main.append(x)
        
        while self.tmp:
            self.main.append(self.tmp.popleft())

    def pop(self) -> int:
        return self.main.popleft()

    def top(self) -> int:
        return self.main[0]

    def empty(self) -> bool:
        return not self.main
  • PUSH
    • main 큐에 있는 모든 값들을 꺼내 tmp 큐로 옮긴다.
    • 비어있는 main 큐에 새로운 값을 추가한다.
    • tmp 큐에 있는 모든 값들을 꺼내 main 큐에 추가한다.
    • main 큐에 있는 모든 값들을 옮기는 시간 + tmp 큐에 있는 모든 값들을 다시 옮기는 시간 이 필요하므로 총 시간 복잡도는 O(N)

  • POP
    • main 큐에서 첫 번째로 값을 꺼내 반환한다.
    • 시간 복잡도 O(1)

배열로 스택과 큐 구현

  • 스택 구현하기

    • 배열의 인덱스가 스택의 top 포인터가 된다.

    • 빈 스택은 top = -1 이다.

    • 꽉 찬 스택은 top = 배열 길이 - 1 이다.

    • PUSH 연산은 top의 값을 1 늘리고, 늘린 top 인덱스가 가리키는 값에 새로운 값을 넣는다.

    • POP 연산은 top 인덱스가 가리키는 값을 반환하고, top 의 값을 1 줄인다.

  • 큐 구현하기

    • 배열의 인덱스가 큐의 front, rear 포인터가 된다.

      • rear 는 비어있는 배열 한 칸의 꼬리 인덱스

      • front 는 차있는 배열 한 칸의 머리 인덱스

    • 비어있는 큐는 front = rear 이다.

    • 꽉 찬 큐는 rear + 1 = front 이다.

      • 배열로 큐를 구현하기 위해선, 아무것도 저장할 수 없는 비어있는 배열 한 칸이 필요하다.

      • 이를 통해 비어있는 큐와 꽉 찬 큐를 구별할 수 있다.

    • PUT 연산은 rear 인덱스가 가리키는 빈 칸에 새로운 값을 넣고, rear 의 값을 1 늘린다.

    • POP 연산은 front 인덱스가 가리키는 값을 반환하고, front 의 값을 1 늘린다.


Prefix, Infix, Postfix

  • prefix (전위표기식)

    • 연산자를 앞에 표기하고, 해당 연산자와 관련된 피연산자를 뒤에 표기하는 방법

    • ex) + A * B C

    • 스택을 사용하여 계산하기 쉽다.

    • 스택을 사용한 계산 방법

      • 전위 표기식을 뒤집는다.

      • 피연산자가 나오면 stack 에 push

      • 연산자가 나오면 stack 의 피연산자 2개를 pop 하여 연산 수행 후, 다시 stack에 push

      • 이를 반복한다.

  • infix (중위표기식)

    • 수학에서 흔히 사용되는 표기법으로, 사람이 수식을 이해하고 사용하기에 편하다.

    • ex) A + B * C

    • 컴퓨터로 계산식을 수행하기는 까다로우므로, 컴퓨터 계산을 원하면 차량기지 알고리즘을 사용하여 infix 를 postfix 로 바꾼다.

  • postfix (후위표기식)

    • 연산자를 뒤에 표기하고, 해당 연산자와 관련된 피연산자를 앞에 표기하는 방법

    • ex) A B C * +

    • 스택을 사용하여 계산하기 쉽다.

      • 컴퓨터가 일반적으로 선호하고, 사용하는 계산식

    • 스택을 사용한 계산 방법

      • 피연산자가 나오면 stack 에 push

      • 연산자가 나오면 stack 의 피연산자 2개를 pop 하여 연산 수행 후, 다시 stack에 push

      • 이를 반복한다.


Deque 구현 방법

  • 이중 연결 리스트를 사용하여 구현한다.

  • Front 포인터의 앞에 값을 추가하고, Front 포인터를 앞으로 이동시키거나 (add Front)

  • Front 포인터의 값을 빼고, Front 포인터를 뒤로 이동시키거나 (remove Front)

  • Rear 포인터의 뒤에 값을 추가하고, Rear 포인터를 뒤로 이동시키거나 (add Rear)

  • Rear 포인터의 값을 빼고, Rear 포인터를 앞으로 이동시키는 (remove Rear) 방식으로 구현


해시 자료구조

  • 키를 값에 매핑하는 자료구조로 배열과 해시 함수를 사용하여 구현한다.

  • 해시 함수는 임의 크기 데이터를 고정 크기 값의 키로 변환하는 함수로, 해시 함수의 변환 결과물을 해시라 한다.

    • hash table 자료구조에서는 입력으로 넣어준 key 에 대한 해시 함수의 변환값이 임의의 정수이다.

    • 이 임의의 정수 (해시값) 을 배열의 크기로 나눈 나머지가 value 가 저장될 배열의 인덱스이다.

    • value 가 저장되는 배열의 각각의 칸을 버킷이라 한다.

  • key 가 다른데 해시값이 같거나, key 도 다르고 해시값도 다른데 해시값 % 배열의 크기 결과가 같은 경우를 해시 충돌이라 한다.


충돌이 최대한 적은 해시 함수

  • 입력 키의 모든 비트를 활용하여 해시값을 생성하도록 한다.

    • 모든 비트를 사용하면 더 많은 고유한 해시값을 만들어 낼 수 있다.

    • 이는 서로 다른 키들이 서로 다른 해시값을 가지도록 보장하여, 충돌의 가능성을 줄인다.


Hash Collision 해결 방법

  • 크게 2가지 해결 방법이 있다.

    • Open Addressing

      • 충돌 발생 시, 탐사를 통해 빈 공간을 찾아나가는 방식이다.

      • 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장이 없다.

      • 전체 버킷 수를 넘어가는 데이터를 넣을 수 없다.

      • 여러가지 방식이 있다.

        • Linear Probing

          • 특정 key 에 대해 해시 충돌이 발생하면, 해당 위치부터 1씩 증가시켜가며 탐사를 하여 빈 버킷을 찾아 데이터를 넣는다.
          • 데이터가 뭉치는 경향이 있어 탐색 성능이 떨어질 수 있으나, 캐시 성능은 좋다.

        • Quadratic Probing

          • 특정 key 에 대해 해시 충돌이 발생하면, 해당 위치부터 1의 제곱, 2의 제곱, .. n의 제곱씩 증가시켜가며 탐사를 하여 빈 버킷을 찾아 데이터를 넣는다.

          • 1차 군집화는 해결하나, 똑같은 점프 시퀸스에 따라 빈 버킷을 찾아내므로 2차 군집화가 발생하는 경향이 있다.

          • 평균적인 캐시 성능을 보인다.

        • Double Hashing

          • 2개의 해시 함수를 사용한다.

          • 특정 key 에 대해 해시 충돌이 발생하면, 해당 key 를 점프 시퀸스를 결정하는 다른 해시함수에 입력으로 넣어줘 점프 시퀸스를 결정한다.

            • 해시 충돌이 발생한 위치부터 앞서 결정한 점프 시퀸스를 곱해주며 탐사를 하여 빈 버킷을 찾아 데이터를 넣는다.

          • (h(key) + n * d(key)) % 해시테이블 크기), n = 0, 1, 2, 3 ...

          • 점프 시퀸스가 다른 해시 함수에 의해 결정되기 때문에 일정하지 않아 군집화가 발생하지 않는다.

          • 그래서 캐시 성능은 떨어진다.

          • 또한 제 2의 해시 함수를 사용하기 때문에 추가적인 계산이 필요하다.

      • Python, 루비가 사용하는 방식

    • Separate Chaining

      • 폐쇄 주소 방식으로 key 에 대한 해시값과 일치하는 곳에 데이터를 계속해서 저장한다.

      • 충돌이 발생해도 key 와 value 쌍을 연결리스트로 연결하며 계속해서 저장한다.

        • 버킷 수와 상관없이 데이터를 무한정 넣을 수 있다.

        • 모든 데이터가 충돌이 발생한 경우 탐색의 시간 복잡도는 O(N) 이 된다.

      • 전통적인 방식으로 구현이 간단하다.

      • 자바, C++, GO가 사용하는 방식


자바의 해시 충돌 처리

  • 자바에서는 해시 충돌이 발생하면 Separate Chaining 방식으로 이를 해결한다.

    • 만약 충돌이 자주 발생하여 연결 리스트의 길이가 8을 넘어가면, 연결 리스트 대신 트리를 사용한다.

    • 연결 리스트의 길이가 6이하이면, 연결 리스트를 사용한다.

      • 트리는 연결 리스트 대비 메모리 사용량이 많고,

      • 적은 수의 노드에서는 트리와 연결 리스트의 성능 차이가 크게 안나기 때문이다.

  • 해시 테이블에 저장된 데이터 개수를 전체 버킷 개수로 나눈 것을 로드 팩터라 한다.

    • 로드 팩터가 증가하면 해시 충돌 가능성이 올라가, 해시 테이블 성능은 감소하게 된다.

    • 자바는 0.75 이하의 로드 팩터를 유지하도록 한다.

    • 만약 0.75 를 넘게 되면, 버킷의 크기를 2배씩 동적 확장한다.


Double Hashing 의 장단점

  • 2개의 해시 함수를 사용한다.

  • 특정 key 에 대해 해시 충돌이 발생하면, 해당 key 를 점프 시퀸스를 결정하는 다른 해시함수에 입력으로 넣어줘 점프 시퀸스를 결정한다.

    • 해시 충돌이 발생한 위치부터 앞서 결정한 점프 시퀸스를 곱해주며 탐사를 하여 빈 버킷을 찾아 데이터를 넣는다.

  • (h(key) + n * d(key)) % 해시테이블 크기), n = 0, 1, 2, 3 ...

  • 장점

    • 점프 시퀸스가 다른 해시 함수에 의해 결정되기 때문에 일정하지 않아 군집화가 발생하지 않는다.

    • 군집화가 발생하지 않기 때문에 충돌 가능성이 적고, 성능이 좋다.

  • 단점

    • 그래서 캐시 성능은 떨어진다.

    • 또한 제 2의 해시 함수를 사용하기 때문에 추가적인 계산이 필요하다.


트리, 이진트리, 이진탐색트리

  • 트리

    • 특수한 형태의 그래프로, 순환 구조를 갖지 않는 그래프이다.

    • 한번 연결된 노드가 다시 연결될 수 없다.

    • 부모 노드가 자식 노드를 가리키는 단방향 뿐이다.

    • 루트 노드를 제외한 트리의 모든 노드들은 하나의 부모 노드를 갖는다.

  • 이진 트리

    • 모든 노드의 자식 노드 개수가 2 이하인 트리

    • 왼쪽, 오른쪽 최대 2개의 자식을 갖는 단순한 형태의 트리이다.

  • 이진 탐색 트리

    • 이진 트리 구조로 이루어져 있다.

    • 모든 노드의 왼쪽 서브 트리는 해당 노드의 값보다 작은 값들만 가지고, 모든 노드의 오른쪽 서브 트리는 해당 노드의 값보다 큰 값들만 가진다.

    • 이러한 규칙을 통해 일반적인 경우에 삽입, 삭제, 탐색의 시간복잡도를 O(log N) 으로 수행할 수 있다.


그래프와 트리의 차이

  • 그래프는 객체간의 관계를 표현하는 자료구조로 순환 구조일 수도 있고, 양방향 그래프일수도 있다.

  • 트리는 그래프의 일종으로, 비순환 구조이고, 단방향 그래프이다.

    • 계층적인 구조를 가진다.

    • 부모 노드가 자식 노드를 가리키는 단방향 뿐이다.

    • 그래프의 부분집합이다.


이진탐색트리에서 중위 순회의 의미

  • 이진 탐색 트리 순회 방법

    • 이진 탐색 트리의 모든 노드들을 한 번씩 방문하는 방법은 대표적으로 4가지가 있다.

    • inorder traversal (중위 순회)

      • 재귀적으로 왼쪽 서브트리 순회

      • 현재 노드 방문

      • 재귀적으로 오른쪽 서브트리 순회

    • preorder traversal (전위 순회)

      • 현재 노드 방문

      • 재귀적으로 왼쪽 서브트리 순회

      • 재귀적으로 오른쪽 서브트리 순회

    • postorder traversal (후위 순회)

      • 재귀적으로 왼쪽 서브트리 순회

      • 재귀적으로 오른쪽 서브트리 순회

      • 현재 노드 방문

    • level-order traversal

      • 큐를 사용하여 노드 레벨 순으로 차례대로 순회

  • inorder traversal (중위 순회) 의 의미

    • inorder traversal 는 이진 탐색 트리에서 가장 작은 값을 가진 노드부터 가장 큰 값을 가진 노드까지 오름차순으로 방문하게 된다.

    • 따라서 이진 탐색 트리의 정렬된 순서를 얻을 수 있다.


이진탐색트리 주요 연산에 대한 시간복잡도

  • 이진탐색트리가 균형잡혀 있다면, 삽입, 삭제, 탐색에 대한 시간복잡도는 O(logN) 이다.

    • 현재 노드를 기준으로 내가 찾고자 하는 값이 왼쪽에 있는지 오른쪽에 있는지 결정할 수 있기 때문에 탐색할 노드 개수가 반으로 줄어들게 된다.

    • 따라서 O(logN) 의 시간 복잡도를 갖는다.

  • 이진 탐색 트리가 한쪽으로 치중되어 있다면, 삽입, 삭제, 탐색에 대한 시간복잡도는 O(N) 이다.

    • 현재 노드를 기준으로 탐색할 노드 개수가 반으로 줄어들지 않고, 한 쪽 방향으로 계속해서 이동하며 모든 노드를 탐색해야 한다.

    • 따라서, 최악의 경우 O(N) 시간 복잡도를 갖는다.


이진탐색트리의 한계점

  • 이진 탐색 트리가 균형잡혀 있다면 주요 연산에 대해 O(logN) 시간 복잡도를 보장할 수 있다.

  • 그러나 이진 탐색 트리가 한쪽 방향으로만 길게 늘어져 있다면 주요 연산의 효율을 크게 떨어뜨린다.

    • 이 경우, 시간 복잡도는 O(N) 이 된다.

이진탐색트리의 값 삽입, 삭제 방법과 편향 발생

  • 삽입

    • 이진 탐색 트리의 규칙을 따르며 값을 집어 넣는다.

    • 즉, 집어 넣으려는 값이 현재 노드보다 작으면 왼쪽 서브트리로, 크면 오른쪽 서브트리로 재귀적으로 이동한다.

    • 가장 말단으로 이동하여 더 이상 자식 노드가 없다면, 해당 부분에 새로운 값 노드를 추가한다.

  • 삭제

    • 특정 노드를 삭제하기 위해 이진 탐색 트리의 규칙을 따르며 값을 탐색한다.

    • 찾은 특정 노드를 삭제한 뒤에도 이진 탐색 트리의 규칙은 유지되어야 한다.

    • 따라서 삭제 동작은 크게 다음과 같은 경우들로 나뉘어 후처리를 해줘야 한다.

      • 말단 노드의 삭제는 그냥 삭제하면 된다.

      • 자식이 한개있는 부모 노드의 삭제는 자식 노드를 삭제 노드 위치를 대신하도록 한다.

      • 자식이 두개있는 부모 노드의 삭제는 삭제하려는 노드를 기준으로 오른쪽 서브트리에서 가장 작은 값을 구한 뒤, 구한 노드가 삭제 노드 위치를 대신하도록 한다.

        • 구한 가장 작은 노드의 오른쪽 서브 트리는 구한 가장 작은 노드의 부모 노드와 연결되어야 한다.

  • 편향 발생

    • 만약 오름차순이나 내림차순으로 정렬된 값을 이진탐색트리에 연속해서 삽입하면 한쪽 방향으로만 길게 늘어진 편향된 이진탐색트리가 만들어진다.

힙

  • 추상 자료형인 우선순위 큐를 구현한 자료형

  • 완전 이진 트리의 형태를 갖는다.

    • 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있고, 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워져 있는 형태의 이진 트리

  • 최소힙이라면 부모의 값은 항상 자식의 값보다 작아야 하고, 최대힙이라면 부모의 값은 항상 자식의 값보다 커야하는 규칙이 있다.

    • 따라서 루트 노드가 힙의 최소값 혹은 최대값이 된다.

  • 최소힙을 기준으로 주요 연산을 설명하면 다음과 같다.

    • heappop

      • 최소값인 루트 노드를 추출한 뒤, 마지막 레벨의 가장 오른쪽 노드를 루트 노드 위치로 올린다.

      • 이후 루트 노드를 힙의 규칙에 맞춰 자식 노드와 크기를 비교하며 아래로 내리면서 정렬한다.

      • 따라서 삭제 연산의 시간 복잡도는 O(logN) 이다.

    • heappush

      • 마지막 레벨의 가장 오른쪽 부분에 노드를 추가한다.

      • 추가한 노드를 힙의 규칙에 맞춰 부모 노드와 크기를 비교하며 위로 올리면서 정렬한다.

      • 따라서 삽입 연산의 시간 복잡도는 O(logN) 이다.


배열로 힙 구현하기

  • 배열의 첫 번째 원소는 사용하지 않는다.

    • arr[0] = INT_MIN

  • 배열의 두 번째 원소가 루트 노드가 된다.

    • arr[1]

  • arr[2], arr[3] 가 arr[1] 의 자식 노드가 된다.

  • arr[4], arr[5] 가 arr[2] 의 자식 노드가 된다.

  • arr[6], arr[7] 가 arr[3] 의 자식 노드가 된다.

  • 즉, arr[idx] 의 부모 노드는 arr[idx//2] 이다.

    • arr[idx] 의 자식 노드는 arr[2 * idx], arr[2 * idx + 1] 이다.

  • 특정 인덱스에 2를 나눈 값이 부모 노드가 되고, 특정 인덱스에서 2를 곱한 값과 2를 곱한 값 + 1 이 자식 노드가 된다.

  • 이런 방식으로 이진 트리 구조인 힙을 배열로 저장할 수 있다.


힙의 삽입, 삭제 방식, 이진탐색트리와 달리 편향이 발생하지 않는 이유

최소힙을 기준으로 설명함

  • 삽입

    • 마지막 레벨의 가장 오른쪽 부분에 노드를 추가한다.

    • 추가한 노드를 힙의 규칙에 맞춰 부모 노드와 크기를 비교하며 위로 올리면서 정렬한다.

      • 추가한 노드 값이 부모 노드보다 작으면 부모 노드와 위치를 바꾼다.

      • 추가한 노드 값이 부모 노드보다 크면 정렬을 종료한다.

    • 비교하는 부모 노드의 최대 개수는 트리의 최대 레벨과 같다.

      • 따라서 삽입 연산의 시간 복잡도는 O(logN) 이다.

  • 삭제 (추출)

    • 최소값인 루트 노드를 추출한 뒤, 마지막 레벨의 가장 오른쪽 노드를 루트 노드 위치로 올린다.

    • 이후 루트 노드를 힙의 규칙에 맞춰 자식 노드와 크기를 비교하며 아래로 내리면서 정렬한다.

      • 자식 노드 중 가장 작은 값을 고른다. (왼쪽 자식 vs 오른쪽 자식)

      • 위로 올린 루트 노드 값이 자식 노드 보다 크면 자식 노드와 위치를 바꾼다.

      • 위로 올린 루트 노드 값이 자식 노드 보다 작으면 정렬을 종료한다.

    • 비교하는 자식 노드의 최대 개수는 트리의 최대 레벨과 같다.

      • 따라서 삭제 연산의 시간 복잡도는 O(logN) 이다.

  • 힙은 완전 이진 트리 구조이기 때문에 편향이 발생하지 않는다.

    • 이진 탐색 트리는 정렬된 값을 넣어주게 되면 편향이 발생한다.

    • 반면, 힙은 데이터를 넣을때 항상 마지막 레벨의 오른쪽 끝에 일단 넣고, 자체적으로 정렬을 수행한다.

    • 또한 삭제시에도 가장 마지막 레벨의 오른쪽 끝에 값을 루트 노드 위치로 올리고, 자체적으로 정렬을 수행한다.

    • 정렬 시 왼쪽 서브트리와 오른쪽 서브트리는 아무런 관계가 없고 부모와 자식간의 규칙만이 있기에 한쪽으로 편향되지 않는다.


힙 정렬의 시간복잡도와 Stable 여부

  • 힙 정렬은 힙 자료구조를 사용한 정렬 방법이다.

    • n 개의 입력을 힙으로 변환하고, 힙 추출을 반복해야 한다.

    • O(N + NlogN)

    • 따라서 O(NlogN) 시간 복잡도이다.

  • 정렬 기준 상 같은 우선순위를 가질때, 먼저 들어온 입력이 먼저 출력되는 정렬 알고리즘을 stable sort 라 한다.

    • stable 이 보장되지 않는다면 unstable sort 이다.

  • 힙 정렬은 대표적인 unstable sort 로, 가장 마지막 레벨의 오른쪽에 있던 값이 한 번에 루트 노드로 이동하고, 정렬되는 과정에서 입력시의 순서가 보장되지 않는 경우가 빈번히 발생한다.


BBST

  • Balanced Binary Search Tree

  • 기존의 이진 탐색 트리는 n개의 입력값에 대해 트리의 높이가 커질 수도 있고 (n-1), 트리의 높이가 작을 수도 있다 (log n).

    • 높이 h 는 log⁡2n≤h≤n−1\log_2 n \leq h \leq n-1 를 만족한다.

  • 이진 탐색 트리의 search, insert, delete 연산은 모두 트리의 높이에 비례하기에 트리의 높이는 중요하다.

  • 이러한 트리 높이의 불균형을 없애고 입력값과 상관없이 트리의 높이를 log⁡2n\log_2 n 과 유사하도록 균형을 잡아가는 이진 탐색 트리가 바로 BBST 이다.

  • BBST 는 트리의 높이를 조절하기 위해 회전을 사용한다.

  • 회전은 O(1) 의 시간 복잡도를 갖는다.

  • 대표적인 BBST 로는 AVL 트리와 Red-Black 트리가 있다.


  • AVL Tree

    • 모든 노드에 대해서 해당 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이차가 1이하여야 한다.

    • 만약 서브트리가 존재하지 않는다면 해당 서브트리의 높이는 -1 로 취급한다.


  • Red Black Tree

    • 노드는 red, black 2가지 상태 중 한 가지를 갖는다.

    • 루트 노드는 black 노드이다.

    • 아무 노드도 존재하지 않는 말단의 노드를 NIL 이라 하며 black 상태로 취급한다.

    • red 노드의 자식 노드는 항상 black 이어야 한다.

      • black 노드는 연속해도 상관없다.

    • 임의의 노드에서 NIL 로 이동하는데 거치는 black 노드의 개수는 항상 같아야 한다.

      • 해당 성질을 만족하기 위해, 삽입되는 노드의 색은 항상 red 이다.

Red Black Tree 의 균형 유지

  • 일단은 이진 탐색 트리와 동일한 방식으로 삽입/삭제를 수행한다.

  • 이후 삽입 노드의 부모 노드부터 방문 노드의 역순으로 차례로 거슬러 올라가며 red-black 트리의 규칙을 만족하지 않는 경우, 이를 만족하도록 트리를 회전시키고 노드들의 색깔을 바꾼다.

  • red-black 트리의 5가지 규칙을 지키려는 과정에서 트리는 편향을 제거하고 균형을 유지하게 된다.


Red Black Tree 의 주요 성질 4가지

  • 노드는 red, black 2가지 상태 중 한 가지를 갖는다.

  • 아무 노드도 존재하지 않는 말단의 노드를 NIL 이라 하며 black 상태로 취급한다.

  • red 노드의 자식 노드는 항상 black 이어야 한다.

  • 임의의 노드에서 NIL 로 이동하는데 거치는 black 노드의 개수는 항상 같아야 한다.

위 4가지 성질을 만족시키면, 루트 노드가 black 노드여야 한다 는 규칙 역시 자동으로 만족된다.


2-3-4 Tree, AVL Tree 등의 다른 BBST 가 있음에도, Red Black Tree가 사용되는 이유

  • 2-3-4 트리의 경우, Red Black 트리로 완전히 대체 가능하다.

    • 그러나 2-3-4 트리는 최대 4개의 자식노드를 가질 수 있으므로, 하나의 노드가 4개의 포인터를 가져야 한다. (공간적인 손해)

    • 또한 이진 트리도 아니고, 삽입/삭제 연산의 구현이 쉽지 않다.

  • AVL 트리의 경우, Red Black 트리 대비 더욱 균형 잡힌 트리를 만들 수 있다.

    • 따라서 Red Black 트리 대비, 탐색 성능이 미묘하게 좋다.

    • 그러나 AVL 트리의 경우, 삽입/삭제 시 리프 노드의 부모 노드부터 루트 노드까지 방문 노드들에 대해 AVL 트리 규칙을 위반하는지 조사해야 한다.

      • 위반 시, rotation 을 통해 트리 구조를 재조정한다.

    • 반면 Red Black 트리는 특정 케이스에서는 방문 노드들에 대한 규칙 위반 조사를 더 이상 진행하지 않는다.

    • 따라서 삽입/삭제 연산에 대해서 Red Black 트리의 성능이 더 좋다.

  • 결론적으로 Red Black 트리가 주로 사용되는 이유는

    • 다른 BBST 대비 구현이 비교적 쉽고

    • 많은 저장공간이 필요하지 않으며

    • 특히 삽입/삭제 가 많이 일어나는 자료구조에 사용하기 좋다.


정렬 알고리즘

  • 입력으로 주어진 배열의 원소들을 오름차순 혹은 내림차순으로 재배치하는 알고리즘

  • 비교횟수와 교환횟수를 최소화하는 것이 좋은 정렬 알고리즘이다.

  • stable 한 알고리즘 vs unstable 한 알고리즘

    • stable 한 정렬 알고리즘은 같은 크기의 수에 대해서 입력 순서를 그대로 유지하며 정렬한다.

    • unstable 한 정렬 알고리즘은 같은 크기의 수에 대해서 입력 순서의 유지를 보장하지 않는다.

  • in-place 알고리즘 vs not in-place 알고리즘

    • in-place 알고리즘은 변수 몇개 정도만 사용하여 정렬한다. (O(1) 공간 복잡도)

    • not in-place 알고리즘은 입력의 크기에 비례하는 추가적인 메모리 공간을 사용하여 정렬한다. (O(N) 공간 복잡도)

  • 따라서 이상적인 정렬 알고리즘은 비교횟수와 교환횟수가 작고, stable 하며, in-place 성질을 갖는 정렬 알고리즘이다.

  • 간단하지만 느린 정렬 알고리즘으로는 bubble sort, selection sort, insertion sort 가 있다.

    • selection sort

      • 매 round 마다 최소값을 찾은 뒤 맨 앞자리부터 차례차례 swap 한다.

      • unstable, in-place 알고리즘

      • swap 빈도가 상대적으로 적다.

      • O(N^2) 시간 복잡도

    • bubble sort

      • 매 round 마다 양 옆의 값을 비교하며 모든 요소를 비교, 교환하여 가장 큰 값을 맨 뒤부터 차곡차곡 쌓는다.

      • stable, in-place 알고리즘

      • swap 횟수가 많아 비효율적인 알고리즘이다.

      • O(N^2) 시간 복잡도

    • insertion sort

      • 매 round 마다 현재 선택된 요소가 앞의 정렬된 요소에 적절한 위치에 삽입되는 방식으로 정렬한다.

      • stable, in-place 알고리즘

      • 정렬이 필요한 경우에만 비교 및 교환 연산을 수행한다.

        • 대부분의 원소가 정렬되어 있는 경우 효율적이다.

      • O(N^2) 시간 복잡도

  • 빠른 정렬 알고리즘으로는 quick sort, merge sort, heap sort, radix sort 등이 있다.

    • quick sort

      • 피벗을 기준으로 피벗보다 작은 값은 왼쪽에, 피벗보다 큰 값은 오른쪽에 있도록 swap 하여 파티셔닝을 한다.

      • unstable, in-place 알고리즘

      • 일반적으로는 파티셔닝을 통해 덩어리를 나누므로 O(NlogN) 시간 복잡도 이지만, 정렬된 입력이 들어오는 경우 O(N^2) 시간 복잡도를 갖는다.

    • merge sort

      • 입력 배열을 더 이상 둘로 쪼갤 수 없을 때까지 분할한다.

      • 분할이 끝나면 각 덩어리들을 둘씩 짝지어 정렬하면서 병합한다.

      • stable, not in-place 알고리즘

      • O(NlogN) 시간 복잡도를 갖는다.

    • radix sort

      • 입력값들이 자연수인 특수한 경우에 사용할 수 있는 알고리즘이다.

      • 최대 자릿수 k를 구한 뒤 1의 자리수부터 k 자리수까지 차례대로 정렬한다.

      • 1의 자리수를 인덱스로 삼아 0~9 버킷에 값들을 넣었다가 차례대로 다시 뺀다.

      • 기준이 되는 자리수를 늘려가며 반복한다.

      • stable, not in-place 알고리즘

      • O(N) 시간 복잡도를 갖는다.

    • heap sort

      • 입력 배열을 힙으로 구조화한뒤 힙에서 모든 값을 pop 하면 정렬된 순서를 얻을 수 있다.

      • unstable, in-place 알고리즘

      • 힙 생성 O(N) + 힙에서 n 개의 원소를 모두 pop 하기 O(NlogN) = O(NlogN) 시간 복잡도를 갖는다.


Quick sort VS Merge sort

  • Quick sort

    • 평균적으로 O(NlogN) 시간 복잡도

    • 정렬되어 있는 값이 입력으로 들어오는 경우 파티셔닝이 제대로 이루어지지 않아 O(N^2) 시간 복잡도가 된다.

    • unstable 하며 in-place 정렬 알고리즘이다.

  • Merge sort

    • 항상 O(NlogN) 시간 복잡도를 갖는다.

    • stable 하며 not in-place 정렬 알고리즘이다.


Quick sort 에서 O(N^2) 이 걸리는 예시와, 이를 개선할 수 있는 방법

  • 가장 우측이나 좌측의 값을 하나 골라 피벗으로 설정하는 일반적인 퀵 정렬에선 오름차순 혹은 내림차순으로 정렬되어있는 입력값이 주어지면, 파티셔닝이 제대로 이루어지지 않아 O(N^2) 시간 복잡도가 걸린다.

  • 따라서 피벗을 결정하는 방식의 변형을 통해 이를 개선할 수 있다.

    • 랜덤으로 피벗을 결정

      • 정렬된 입력값이 항상 O(N^2) 의 시간 복잡도가 걸리는 것을 막을 수 있다.

      • 아주 낮은 확률이지만 O(N^2) 의 최악의 case 가 발생할 수도 있다.

    • Median-Of-3 Method

      • 입력값의 가장 좌측, 가장 우측, 중앙값 3가지를 고른 뒤, 그 중 중간값을 골라 피벗으로 결정한다.

      • 이렇게 고른 중간값은 적어도 최대, 최소값은 아니기에 O(N^2) 의 최악의 case 발생을 막을 수 있다.


Stable Sort 의 개념과 Stable 한 정렬 알고리즘

  • Stable Sort 란 같은 크기를 가진 입력값들을 입력 순서와 동일하게 정렬하는 것을 말한다.

  • 반대되는 성질의 알고리즘은 unstable sort 로 이 경우엔 같은 크기를 가진 입력값들이 입력 순서와 동일하게 정렬되는 것을 보장하지 않는다.

  • Stable 한 정렬 알고리즘으로는 bubble sort, insertion sort, merge sort, radix sort 등이 있다.


Merge sort 비재귀 구현

  • 재귀를 사용하는 방식이 큰 덩어리를 반 씩 쪼개가며 정렬하는 Top-Down 방식이라면

    • 비재귀 방식은 작은 부분 배열을 둘 씩 합쳐가며 정렬하는 Bottom-Up 방식이다.

  • 부분 배열 크기 size 를 1, 2, 4, 8 .. 이런식으로 두 배씩 증가시킨다.

    • 그 안에서 low 인덱스는 왼쪽 부분 배열의 시작 인덱스를

    • mid 인덱스는 low 인덱스 + size - 1 로 왼쪽 부분 배열의 끝 부분 인덱스를 (두 부분 배열의 가운데 인덱스)

    • high 인덱스는 low 인덱스 + 2 * size -1 과 입력값의 마지막 인덱스 중 작은 값으로, 오른쪽 부분 배열의 끝 부분이거나 입력값의 마지막 인덱스를 의미한다.

  • 이렇게 구한 low, mid, high 인덱스를 사용해 작은 부분 배열 2개를 합치면서 정렬된 큰 배열을 만든다.

  /**
   * 주어진 a 배열을 정렬한다.
   */
  void bottomUpMergeSort(int[] a) {
    int N = a.length;
    aux = new int[N];
    for (int size = 1; size < N; size = size + size) {
      // size: 서브 배열의 크기
      for (int lo = 0; lo < N - size; lo += size + size) {
        // lo: 왼쪽 서브 배열의 시작 인덱스
        merge(a, lo, lo + size - 1, Math.min(lo + size + size - 1, N - 1));
      }
    }
  }


  /**
   * 주어진 a 배열의 sub 배열 a[lo..mid]와 sub 배열 a[mid+1..hi]를 병합합니다.
   *
   * @param a   배열
   * @param lo  첫번째 sub 배열 시작 인덱스
   * @param mid 첫번째 sub 배열 마지막 인덱스
   * @param hi  두번째 sub 배열 마지막 인덱스
   */
void merge(int[] a, int lo, int mid, int hi) {
    //  a[lo..hi]를 aux[lo..hi]에 복제
    for (int k = lo; k <= hi; k++) {
      aux[k] = a[k];
    }

    int i = lo;       // sub 배열 1 인덱스
    int j = mid + 1;  // sub 배열 2 인덱스

    // 다시 a[lo..hi]로 병합
    for (int k = lo; k <= hi; k++) {
      if (i > mid) {
        // sub 배열 1 인덱스가 마지막까지 갔다면 sub 배열 2의 값을 선택해 넣는다
        a[k] = aux[j++];
      } else if (j > hi) {
        // sub 배열 2 인덱스가 마지막까지 갔다면 sub 배열 1의 값을 선택해 넣는다
        a[k] = aux[i++];
      } else if (aux[j] < aux[i]) {
        // 두 sub 배열 헤드 중 작은 값을 선택해 넣는다
        a[k] = aux[j++];
      } else {
        // 두 sub 배열 헤드 중 작은 값을 선택해 넣는다
        a[k] = aux[i++];
      }
    }
  }

Radix sort

  • 입력 값들이 자연수인 특수한 경우에 사용할 수 있는 알고리즘이다.

  • 최대 자리수 k 를 구한 뒤 1의 자리수부터 k 자리수까지 차례대로 정렬한다.

    • 1의 자리수를 인덱스로 삼아 0~9 버킷에 값들을 넣었다가 차례대로 다시 뺀다.

    • 기준이 되는 자리수를 늘려가며 반복한다.

  • stable, not in-place 알고리즘

  • O(N) 시간 복잡도를 갖는다.

입력 값


1의 자리수 기준으로 버킷에 넣었다가 차례대로 빼 정렬한다.


10의 자리수 기준으로 버킷에 넣었다가 차례대로 빼 정렬한다.


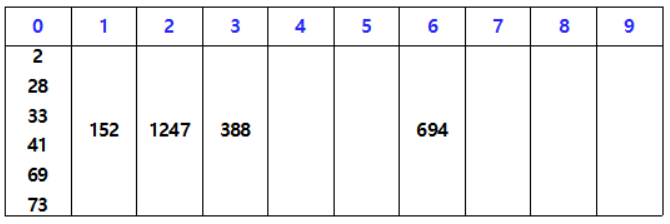
100의 자리수 기준으로 버킷에 넣었다가 차례대로 빼 정렬한다.


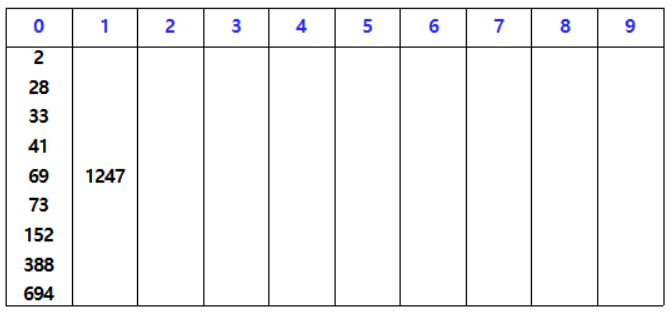
1000의 자리수 기준으로 버킷에 넣었다가 차례대로 빼 정렬한다.


Bubble sort, Selection sort, Insertion sort 의 성능 비교

  • Bubble sort

    • 어떤 입력이 주어지더라도 n(n-1)/2 번 비교해야 한다.

    • 정렬된 입력이 주어지면 swap 하지 않는다.

    • 역정렬된 입력이 주어지는 최악의 경우에 n(n-1)/2 번 swap 한다.

    • 많은 비교와 swap 이 필요한 비효율적인 알고리즘이다.

  • Selection sort

    • 어떤 입력이 주어지더라도 n(n-1)/2 번 비교해야 한다.

    • 정렬된 입력이 주어지면 swap 하지 않는다.

    • 역정렬된 입력이 주어지거나 최악의 경우에도 n-1 번을 넘는 swap 이 발생하지는 않는다.

    • swap 횟수가 최악의 경우에도 상대적으로 적기에 역정렬된 입력이나 거의 정렬되지 않은 입력이 주어질 때 효율적이다.

  • Insertion sort

    • 역정렬된 입력이 주어지는 최악의 경우 n(n-1)/2 번 비교해야 한다.

    • 역정렬된 입력이 주어지는 최악의 경우 n(n-1)/2 번 swap해야 한다.

    • 정렬된 입력이 주어지는 최선의 경우 n-1 번만 비교한다.

    • 정렬된 입력이 주어지는 경우 swap 이 발생하지 않는다.

    • 정렬된 입력이나 거의 정렬된 입력이 주어질 때 비교횟수가 적어 효율적이다.

따라서 Bubble sort 는 가장 느리고, 입력값의 정렬된 수준에 따라 Insertion sort 와 Selection sort 는 성능 차이가 있다. 그러나 캐시까지 고려한 참조 지역성의 원리를 고려하면 인접한 메모리와의 비교를 수행하는 insertion sort 가 가장 효율적이라 할 수 있다.


값이 거의 정렬되었거나, 정렬된 입력에 대해서 Bubble sort, Selection sort, Insertion sort 의 성능 비교

  • 값이 거의 정렬된 경우엔 insertion sort 가 selection sort 보다 비교횟수가 적기 때문에 효율적이다.

자바의 정렬 알고리즘

  • 자바는 정렬하려는 값이 무슨 타입이고 길이가 얼마나 되는지에 따라 정렬 알고리즘이 바뀐다.

  • 배열을 정렬하는 Arrays.sort() 의 경우

    • int, long 과 같이 숫자 범위가 큰 경우

      • Dual-Pivot Quick Sort 사용

    • short, char, byte 처럼 숫자 범위가 작은 경우

      • 입력값의 길이가 크면 Counting Sort 사용

      • 입력값의 길이가 작으면 Dual-Pivot Quick Sort 사용

    • Object 배열의 경우

      • Tim Sort 사용

      • legacy 옵션으로 Merge Sort 사용도 가능

  • ArrayList 나 LinkedList 같은 컬렉션을 정렬하는 Collections.sort() 역시 Object 타입을 원소로 갖기에 Object 배열의 정렬과 같다.

  • 자바에서 사용하는 Dual-Pivot Quick Sort 는 작은 길이의 입력에 대해서는 Insertion Sort 를 사용하고, 긴 길이의 입력에 대해서는 Dual-Pivot Quick Sort 를 사용해 작은 길이의 파티션으로 분할한다.

    • Dual-Pivot Quick Sort 는 가장 왼쪽과 가장 오른쪽을 피벗으로 설정한 뒤, 둘을 비교해 작은 값을 좌측 피봇으로 설정한다.

    • 그 후 값들을 순회하며 좌측 피봇보다 작은 영역, 좌측 피봇과 우측 피봇 사이의 영역, 우측 피봇보다 큰 영역으로 나누며 세 부분으로 분할한다.

    • 이 과정을 반복한다.

    • Dual-Pivot Quick Sort 는 피벗 주변에서 데이터의 위치 이동이 빈번하게 발생하기에 참조 지역성이 좋다.

    • 또한 in-place 정렬 알고리즘이다.

    • 그러나 최악의 경우 O(N^2) 이 될 수 있다.

  • Object 배열은 참조 지역성을 살려 정렬하기 어려우므로 Tim Sort 를 사용한다.

    • Tim Sort 는 Insertion Sort 와 Merge Sort 를 합쳐 변형한 정렬 알고리즘이다.

    • Insertion Sort 를 사용하여 2^5 ~ 2^6 크기의 오름차순 덩어리 run 을 만든다.

    • 각각의 run 들을 규칙에 맞춰 병합한다.

    • Tim Sort 는 진행과정에서 여러 시간적/공간적 최적화 기법이 사용되어 뛰어난 성능을 내는 정렬 알고리즘이다.

    • stable, not in-place, O(NlogN) 의 시간 복잡도를 갖는 알고리즘이다.


정렬해야 하는 데이터가 50G 인데, 메모리가 4G라면 어떤식으로 정렬해야 할까?

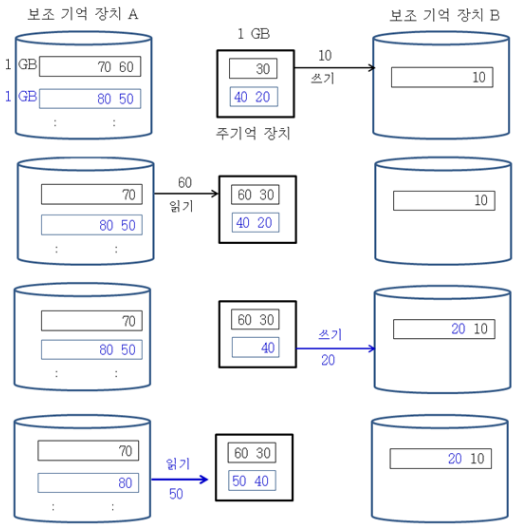
  • 보조 기억 장치의 50G 데이터를 4G 크기의 블록들로 나눈다.

  • 블록들을 하나씩 메모리로 읽어와 정렬한 후 보조 기억 장치로 다시 저장하는 작업을 반복하여 정렬된 각각의 블록들을 만든다.

  • 정렬된 블록 2개에서 각각 2G 만큼만 부분적으로 메모리로 읽어들인 뒤, 가장 작은 값을 보조 기억 장치에 8G 블록에 저장한다.

  • 보조 기억 장치에 저장한 가장 작은 값은 메모리에서 제거하고, 가장 작은 값을 갖고 있던 보조 기억 장치의 4G 블록에서 값을 더 읽어온다.

  • 이를 반복하여 정렬된 8G 블록을 만들 수 있다.

  • 위 과정을 반복하면 50G 데이터를 정렬할 수 있다.


그래프와 그래프의 구현 방법

  • 그래프는 객체간의 관계를 표현하는 자료구조이다.

  • 그래프를 표현하는 방법은 크게 두 가지가 있다.

    • Adjacency Matrix (인접 행렬)

      • 노드 개수가 N 개라고 하면 N*N 행렬을 만들어 그래프를 표현한다.

      • (x, y) 지점이 1이라면 x 노드는 y 노드와 직접 연결됨을 의미한다.

      • (x, y) 지점이 0이라면 x 노드는 y 노드와 직접 연결되지 않았음을 의미한다.

      • sparse 한 그래프라면 인접 행렬의 대부분이 의미없는 0으로 채워져있어 메모리 낭비가 심하다.

    • Adjacency List (인접 리스트)

      • 노드 개수가 N 개라고 하면 N 개의 크기를 갖는 배열을 만들어 그래프를 표현한다.

      • x 번째 배열에 x 번째 노드와 직접 연결된 노드들을 연결리스트로 저장한다.


그래프 표현 방법간의 성능 비교

  • Adjacency Matrix

    • 주어진 노드가 N 개 일때, N*N 행렬을 만들어야 하기 때문에 O(N^2) 공간 복잡도를 갖는다.

    • 두 노드 u, v 가 연결되었는지 확인하려면 G[u][v] == 1 인지만 체크하면 되므로 O(1) 시간 복잡도를 갖는다.

    • 노드 u 에 인접한 모든 노드들을 확인하려면 u 번째 row 에 대해 for 문을 돌아 확인하므로 O(N) 시간 복잡도를 갖는다.

    • 그래프의 모든 값들을 순회하려면 O(N^2) 시간 복잡도를 갖는다.

  • Adjacency List

    • 주어진 노드가 N 개, 간선의 개수가 E개 라면 N 길이의 행렬을 만들고 E개 만큼 연결리스트로 연결되기 때문에 O(N+E) 공간 복잡도를 갖는다.

    • 두 노드 u, v 가 연결되었는지 확인하려면 G[u] 와 연결된 인접리스트 중 v 노드가 존재하는지 찾아야 하므로 O(N) 시간 복잡도를 갖는다.

    • 노드 u 에 인접한 모든 노드들을 확인하려면 G[u] 와 연결된 인접리스트를 모두 돌며 확인하므로 O(N) 시간 복잡도를 갖는다.

    • 그래프의 모든 값들을 순회하려면 O(N+E) 시간 복잡도를 갖는다.


정점의 개수가 N개, 간선의 개수가 N^3 개라면 어떤 방식이 효율적일까?

  • dense 한 그래프는 adjacency list 로 구현하면 공간 복잡도와 시간 복잡도 상에서 비효율적이다.

    • 공간 복잡도 O(N+N^3) = O(N^3)

    • 그래프의 모든 지점을 순회하는 시간 복잡도 O(N+N^3) = O(N^3)

  • 따라서 dense 한 그래프는 adjacency matrix 로 구현하는 것이 효율적이다.

    • 공간 복잡도 O(N^2)

    • 그래프의 모든 지점을 순회하는 시간 복잡도 O(N^2)


사이클이 없는 그래프는 모두 트리인가?

  • 트리의 특징은 다음과 같다.

    • 그래프가 모두 연결되어 있다.

    • cycle 이 없다.

    • 노드 간의 계층 구조를 갖는다.

  • 따라서 다음의 조건을 모두 만족하지 않는 cycle 이 없는 그래프는 트리가 아니다.

  • ex) 모든 그래프가 연결되지 않고 섬이 존재하는 그래프


그래프에서의 최단거리 알고리즘

  • BFS

    • 가중치와 방향이 없는 그래프에서 사용할 수 있다.

  • Dijkstra Algorithm

    • 그리디 알고리즘을 사용한다.

    • 음의 가중치가 없는 그래프에서 사용가능하다.

    • 현재 노드에서 갈 수 있는 모든 경로 (노드, 가중치) 를 최소힙에 저장한다.

      • 최소힙에 저장되는 가중치는 현재 노드까지의 가중치 값 + 현재 노드에서 갈 수 있는 노드로의 가중치 값으로 갱신된다.

    • 최소힙에서 가중치가 가장 작은 최적의 경로를 꺼낸다.

    • 최적의 경로로 이동하여 해당 노드에서 위의 과정들을 반복한다.

    • 한 번 방문한 노드는 두번 다시 방문하지 않는다.

      • 특정 노드에 방문할 때의 비용이 최단거리 비용이다.

    • 이를 통해 시작 노드 기준으로 모든 노드로의 최단 경로를 알 수 있다.

      • 1-to-all 알고리즘

    • adjacency list 의 BFS 시간 복잡도는 O(V+E) 이고, heap 의 삽입-삭제 시간복잡도는 O(logE) (일반적인 경우 V^2 > E 이므로 O(logV) 로 표현하기도 한다.)

      • 따라서 Dijkstra 알고리즘의 시간 복잡도는 O((V+E)logE) 
def dijkstra(start):
    heap = []
    heapq.heappush(heap, (0, start))

    while heap:
        weight, current = heapq.heappop(heap)

        if visit[current]:          # 이미 방문한 노드면, 최단거리가 정해졌으므로 continue
            continue

        visit[current] = True
        dist[current] = weight          # 현재 노드의 최단 거리 설정
        for v, w in graph[current]:
            if not visit[v]:        # 현재 노드에서 아직 방문하지 않은 노드들의 경로를 최소힙에 push
                heapq.heappush(heap, (w + dist[current], v))

  • Bellman-Ford Algorithm

    • DP 를 사용한다.

    • 음의 가중치가 있는 그래프에서도 사용가능하다.

      • 음의 cycle 을 감지할 수 있다.

    • 시작 노드를 정한 뒤, 모든 간선들을 순회하며 다른 노드로 가는 최소 비용을 계산하여 최단거리 테이블을 갱신한다.

    • 이를 전체 노드 개수 V - 1 번 반복한다.

      • 시작 노드에서 어떤 노드라도 V-1 개의 경로를 통해 갈 수 있기 때문이다.

    • V-1 번 반복하므로 O(V), 모든 E를 순회하므로 O(E)

      • 따라서 총 시간복잡도는 O(VE)
def bellman_ford(start):
    dist[start] = 0

    for _ in range(v - 1):      # 노드 개수 - 1 만큼 반복
        for edge in edges:          # 모든 edge 에 대해 반복
            v1, v2, w = edge
            if dist[v2] > dist[v1] + w:
                dist[v2] = dist[v1] + w

  • Floyd-Warshall Algorithm

    • DP를 사용한다.

    • 음의 가중치가 있는 그래프에서도 사용가능하다.

    • 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산한다.

    • Dijkstra 와 유사하나, 방문하지 않은 노드 중 최단거리를 찾지 않는다.

      • 모든 노드에 대해 최단거리 갱신을 반복

    • a 에서 b로 가는 최단거리 > a 에서 k 를 거쳐 b로 가는 거리 이면 a 에서 k 를 거쳐 b 로 가도록 최단 거리를 갱신한다.

    • 전체 노드 개수 V의 삼중 반복이 필요하므로 O(V^3) 시간복잡도를 갖는다.

def floyd_warshall():
    for k in range(1, v+1):         # 모든 노드 개수에 대한 삼중 반복문
        for a in range(1, v+1):
            for b in range(1, v+1):
                graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

  • A* Algorithm

    • Heuristic Algorithm

    • 각 지점에서 도착 지점까지의 거리를 추정한 값을 가지고 최단거리를 결정할 때 같이 사용한다.

    • 시작 지점에서 특정 지점까지의 거리를 g(x), 특정 지점에서 도착 지점까지의 추정 거리를 h(x) 라 할 때, 알고리즘 상에서의 다음 방문 노드는 g(x) + h(x) 값이 최소가 되는 노드이다.

      • 이러한 노드들을 계속 방문하여 목적지 노드에 도착하면 경로 탐색을 종료한다.

트리에서의 최단거리 알고리즘

  • 트리를 이루는 노드는 단 하나의 부모를 가진다.

  • LCA (Lowest Common Ancestor) 알고리즘을 사용하여 두 노드의 가장 가까운 공통 부모를 찾는다.

    • 두 노드의 depth 를 같게 맞춰준 뒤, 하나씩 위로 거슬러 올라가며 가장 가까운 공통부모를 찾는 알고리즘

  • 각 노드로부터 공통 부모로까지의 거리의 합이 두 노드의 최단거리이다.


다익스트라 알고리즘에서 힙을 사용하지 않는 경우 시간복잡도

  • 힙을 사용하지 않고, 현재 노드에서의 최적의 경로를 가진 노드를 선형탐사한다면

  • 최악의 경우 V개의 노드에 대해서 V-1 개의 노드에 대해 검사해야 하므로 O(V^2) 시간복잡도를 갖는다.


정점의 개수가 N개, 간선의 개수가 N^3 개일 때, 효율적인 알고리즘

  • 힙을 사용한 다익스트라 알고리즘은 O((V+E)logE) 시간복잡도이므로 다음의 경우에 O(N^3logN) 시간복잡도를 갖는다.

  • 힙을 사용하지 않은 다익스트라 알고리즘은 O(V^2) 시간복잡도이므로 다음의 경우에 O(N^2) 시간복잡도를 갖는다.

  • 따라서 노드 개수 대비 간선이 많은 경우엔 힙을 사용하지 않고 선형 탐사하는 다익스트라 알고리즘이 효율적이다.


A* 알고리즘과 다익스트라 알고리즘의 성능 비교

  • 다익스트라 알고리즘은 하나의 시작 노드에서 모든 경로에 대한 최단 거리를 정확하게 계산하는 1-to-all 알고리즘이다.

    • 따라서 A* 알고리즘 대비 느리나, 정확하다.

  • A* 알고리즘은 모든 노드에서 도착 노드까지의 추정치를 바탕으로

    • 현재 노드에서 특정 노드까지의 실제거리와

    • 특정 노드에서 도착 노드까지의 추정 거리의 합이

    • 최소가 되는 지점들만 골라서 이동하는 1-to-1 알고리즘이다.

    • 따라서 다익스트라 알고리즘 대비 빠르나 부정확할 수 있다.


음수 간선이 있을 때와, 음수 사이클이 있을때의 최단거리 알고리즘

  • 음수 간선이 있을 경우

    • 다익스트라 알고리즘 사용 불가

    • Bellman-Ford, Floyd-Warshall 알고리즘은 사용할 수 있다.

  • 음수 사이클이 있는 경우

    • Bellman-Ford 알고리즘을 이용하여 음수 사이클의 존재 여부는 체크할 수 있다.

    • 음수 사이클이 존재하면 경로 비용이 음의 무한대로 발산하므로 최단거리 알고리즘은 사용할 수 없다.


재귀함수

  • 함수 안에서 자신의 함수를 다시 호출하는 함수

  • 일반적으로 종료 조건이 있다.

    • 재귀함수를 내부적으로 반복하다가 종료 조건을 만족하면 더 이상 재귀호출을 하지 않고 결과를 반환한다.

재귀함수의 동작 과정

  • 재귀함수는 자신의 스택프레임에 caller 함수로 돌아갈 복귀주소 값 ($ra), 매개변수로 넘어온 변수 ($a0, $a1 ..) 를 저장하고 시작한다.

  • 만약 종료 조건을 만족했다면 스택프레임에 저장된 변수들을 제거하고 복귀 주소로 jump 한다.

    • 현재 함수에서의 스택프레임이 제거된다.

  • 종료 조건을 만족하지 않았다면

    • 재귀 함수의 내부로직을 진행하며 변수들을 자신의 스택프레임에 저장한다.

    • 현재 재귀함수에서의 복귀할 주소를 $ra 레지스터에 저장하고 다시 재귀함수를 호출한다.

    • 호출된 재귀함수는 다시 새로운 스택프레임을 caller 재귀함수의 스택프레임 위에 쌓고 위 과정을 반복한다.


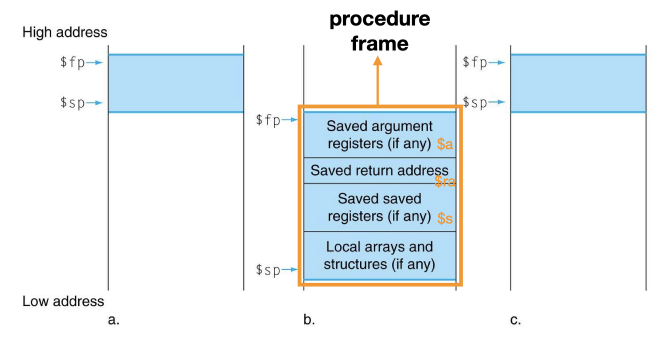
재귀함수의 최적화

  • 꼬리재귀를 사용하는 경우 컴파일러의 옵션에 따라 최적화가 될 수 있다.

    • 컴파일러는 꼬리재귀코드를 재귀 호출의 반복에 의해 스택이 깊어지지 않도록 반복문으로 바꿔 최적화한다.

  • 꼬리재귀란 반환값에서 연산이 없는 재귀함수를 의미한다.

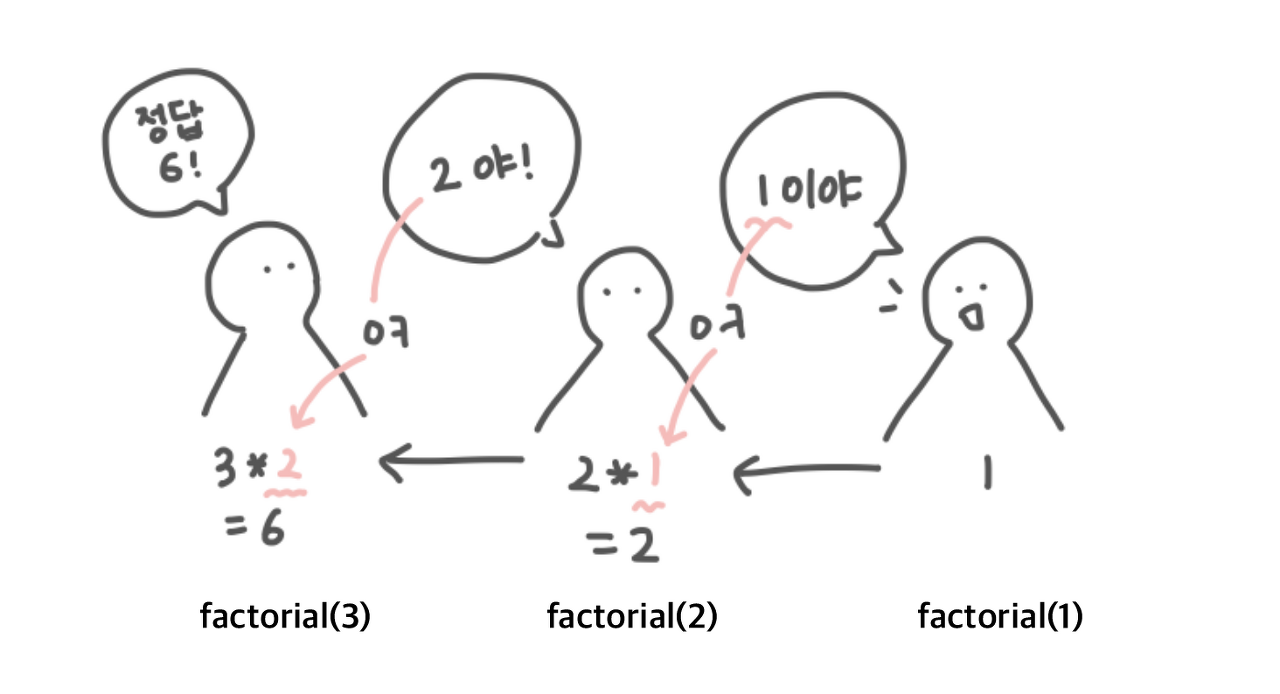
function factorial(n) {
    if (n === 1) {
        return 1;
    }
    return n * factorial(n-1);
}

일반재귀


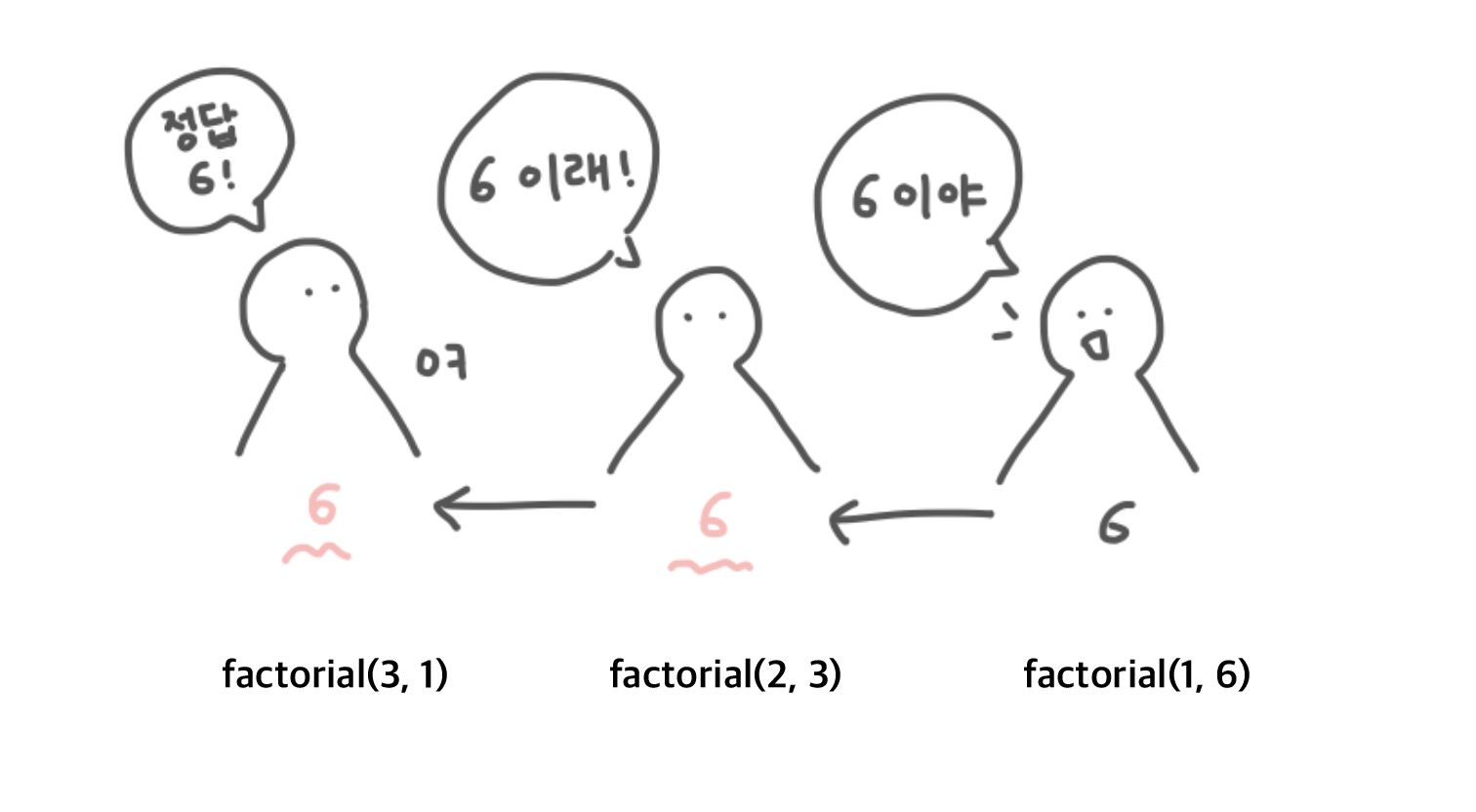
function factorial(n, total = 1){
    if(n === 1){
        return total;
    }
    return factorial(n - 1, n * total);
}

꼬리재귀


MST

  • Minimum Spanning Tree

  • 무방향 가중치 그래프에서 모든 정점을 포함하면서, 가중치의 합이 최소인 트리

  • Prim's Algorithm 과 Kruskal's Algorithm 이 있다.

  • Prim's Algorithm

    • 연결된 그래프에서만 제대로 동작한다.

    • Cut Property 를 이용하여 MST를 만든다.

      • 두 서브트리를 연결하는 여러개의 경로 중 최소 비용의 경로를 포함하는 MST는 항상 존재한다.

    • 현재 선택된 정점 집합에서 연결된 간선 중 최소 비용을 가진 간선을 선택하여 MST를 만든다.

      • 선택된 간선의 노드는 정점 집합에 추가한다.

      • 선택된 간선은 저장한다.

    • 선택된 간선의 개수가 전체 노드 개수 V - 1 이 될 때까지 과정을 반복한다.

      • 선택된 간선 V-1 개가 MST이다.

    • 최소 비용을 가진 간선을 선택할 때 heap 을 사용하면 O((V+E)logE) 시간복잡도를 갖는다.

  • Kruskal's Algorithm

    • 연결되어 있지 않은 그래프에서도 동작한다.

    • Cycle Property 를 이용하여 MST를 만든다.

      • 임의의 cycle 의 최대 비용 간선은 MST에 포함되지 않는다.

    • 간선들의 가중치를 오름차순으로 정렬한다.

    • 가장 작은 가중치부터 선택하면서 MST를 만든다.

      • 사이클이 형성되지 않도록 간선을 선택한다.

      • 사이클을 만드는 간선은 사이클의 최대 비용 간선이기 때문이다.

      • 이때 사이클 여부를 검사하기 위해 Union-Find 자료구조를 사용한다.

    • 선택된 간선의 개수가 전체 노드 개수 V - 1이 되면 반복을 종료한다.

    • 간선들을 정렬하는 시간복잡도 O(ElogE) , cycle 을 검증하는 작업이 간선수에 비례하여 필요하므로 O(ElogV)

      • 따라서 총 시간복잡도는 O(ElogE)

Union-Find 자료구조

  • Disjoint-Set (서로소 집합) 알고리즘

  • 여러개의 노드가 존재할 때 두개의 노드가 서로 같은 그래프에 속하는지 판별한다.

  • 각 노드의 부모 노드를 저장하는 parent 테이블을 만든다.

    • 모든 노드들은 맨 처음에 자기 자신을 parent 로 갖는다.

  • 두 노드를 하나로 합치는 Union 과정에서는 재귀함수를 이용하여 두 노드의 루트노드를 구한 뒤, 한쪽 루트노드를 다른쪽 루트노드의 자식으로 넣는다.

    • 두 루트노드를 합칠 땐, 높이가 큰 트리의 루트노드를 부모로 하고, 높이가 작은 트리의 루트노드를 자식으로 하여 합치는 것이 좋다.

  • 두 노드가 같은 집합에 속하는지 판별하는 Find 연산에서는 두 노드의 parent 테이블을 참조하여

    • parent (루트노드) 가 같다면 같은 집합

    • parent 가 다르다면 다른 집합임을 알 수 있다.

  • root 를 찾기위해 트리의 깊이만큼 재귀를 반복하므로 O(logN) 시간복잡도를 갖는다.

  • 크루스칼 알고리즘에서는 cycle 여부를 검사하기 위해 사용한다.

    • 만약 추가하려는 간선의 두 노드가 같은 root parent 를 갖는다면 cycle 이므로 해당 간선을 추가하지 않는다.

Prim Algorithm vs Kruskal Algorithm

  • Prim 알고리즘은 현재 노드를 기준으로 주변의 노드들의 경로를 계산하며 MST를 만든다.

    • 노드 기준으로 알고리즘이 수행되기에 노드 개수가 적고 간선 개수가 많은 dense 그래프에서 성능이 좋다.

  • Kruskal 알고리즘은 모든 간선들을 정렬하고 최적의 간선들을 골라가며 MST를 만든다.

    • 간선 기준으로 알고리즘이 수행되기에 노드 개수가 많고 간선 개수가 적은 sparse 그래프에서 성능이 좋다.

Prim 과 Kruskal 알고리즘의 결과물

  • Prim 알고리즘은 한번 방문한 노드를 더 이상 방문하지 않는다.

    • Cycle 이 생기지 않는다.

  • Prim 알고리즘은 N개의 모든 노드를 방문하며 N-1개의 간선이 생길 때 알고리즘을 종료한다.

    • 트리는 N개의 노드가 N-1 개의 간선으로 모두 연결되어 있다.

  • Kruskal 알고리즘은 Cycle Property 를 이용한다.

    • Cycle 이 생기지 않는다.

  • Kruskal 알고리즘에서 비연결된 그래프는 알고리즘 진행 과정에서 반드시 연결된다.

    • 모든 노드들이 연결된다.

  • Kruskal 알고리즘은 N-1개의 간선이 생길 때 알고리즘을 종료한다.


따라서 두 알고리즘의 결과물은 반드시 트리이다.


Thread Safe 자료구조

자바 기준으로 설명합니다.

  • Collections.synchronizedXXX 메서드로 기존 컬렉션을 감싸 Thread Safe 자료구조를 만들 수 있다.

    • 자료구조 접근 시, 하나의 스레드가 전체 자료구조에 락을 건다.

    • 따라서 전체 자료구조를 segment 로 나눠 부분적인 락을 거는 concurrent 패키지의 자료구조 대비 느리다.

  • ConcurrentHashMap 과 같은 concurrent 패키지의 자료구조

    • ConcurrentHashMap 의 경우 자바 8 이전엔 16개의 segment로 나눠 락을 걸었지만, 자바 8 이후엔 각 버킷당 하나의 락을 갖도록 세분화되었다.

      • 동시성 증가

  • Atomic 자료구조

    • AtomicInteger, AtomicLong 등이 있다.

    • CAS 방식을 사용한다.

      • 만약 CAS 가 성공하면 연산을 성공적으로 마친것이고

      • CAS 가 실패한다면 연산을 취소하고 처음부터 다시 한다.

    • Lock 을 걸지 않기 때문에 Synchronized 를 사용하는 경우보다 빠르다.


CAS (Compare-And-Swap)

  • 이전값과 새로운 값을 전달한다.

  • 이전값과 현재 메모리에 저장된 값이

    • 같은 경우, 메모리의 값을 새로운 값으로 변경하고 true 반환

    • 다른 경우, 아무 동작도 하지 않고 false 반환

  • lock-free 알고리즘으로, 락을 사용하지 않고 여러 스레드간의 동기화를 수행한다.


배열의 길이를 안다면, 더 빠른 Thread Safe 자료구조를 만들 수 있을까?

  • AtomicIntegerArray 와 같은 Atomic 정적 배열을 사용하여 락을 걸지 않고 더 빠른 Thread Safe 자료구조를 만들 수 있다.

문자열 자료구조 & 알고리즘

Trie

  • 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조

  • 각각의 문자 단위로 색인을 구축한다.

    • 문자 개수만큼 노드가 필요하기 때문에 저장공간의 크기가 크다.

  • 저장된 단어 개수와 상관없이, 트라이 탐색은 찾는 문자열의 길이 만큼만 탐색하면 된다.

  • 예시

    • 비어있는 트라이에 abc 를 저장한다고 가정

      • key 가 a 인 노드를 만든다.

      • a 의 자식 노드로 key 가 b 인 노드를 만든다.

      • b 의 자식 노드로 key 가 c 인 노드를 만든다.

      • c 노드의 data 에 abc 문자열을 넣는다.

    • 이후, 트라이에 abd 를 저장한다고 가정

      • key 가 a 인 노드를 찾는다.

      • a 의 자식 노드 중 key 가 b 인 노드를 찾는다.

      • b 의 자식 노드 중 key 가 d 인 노드를 찾는다.

      • d 인 자식 노드가 없으므로 자식 노드 d 를 만든다.

      • d 노드의 data 에 abd 문자열을 넣는다.

    • 문자열을 찾을 때는 입력 문자열에 맞는 노드를 찾아가며 이동한다.

      • 만약 해당되는 노드가 없어 탐색이 끊기거나, 탐색을 완료한 노드에 data 가 없으면 입력 문자열은 존재하지 않는 것이다.
class Node:
    def __init__(self, key, data=None):
        self.key = key
        self.data = data
        self.children = {}


class Trie:
    def __init__(self):
        self.head = Node(None)

    # 문자열 삽입
    def insert(self, string):
        curr_node = self.head

        for char in string:
            # 자식Node들 중 같은 문자가 없으면 Node 새로 생성
            if char not in curr_node.children:
                curr_node.children[char] = Node(char)

            # 같음 문자가 있으면 노드를 따로 생성하지 않고, 해당 노드로 이동
            curr_node = curr_node.children[char]

        # 문자열이 끝난 지점의 노드의 data값에 해당 문자열을 표시
        curr_node.data = string


    # 문자열이 존재하는지 탐색
    def search(self, string):
        # 가장 아래에 있는 노드에서부터 탐색 시작한다.
        curr_node = self.head

        for char in string:
            if char in curr_node.children:
                curr_node = curr_node.children[char]
            else:
                return False

        # 탐색이 끝난 후에 해당 노드의 data값이 존재한다면
        # 문자가 포함되어있다는 뜻이다!
        if curr_node.data:
            return True

KMP

  • 주어진 문자열 N과 검색하고 싶은 문자열 M 이 주어질 때, 기존 Brute-Force 를 사용한 문자열 검색 알고리즘은 O(NM) 시간 복잡도를 갖는다.

  • KMP 알고리즘은 O(N+M) 시간 복잡도로 M의 위치들을 찾을 수 있다.

    • 주어진 문자열 N을 순회하는 인덱스가 절대 감소하지 않기 때문에 O(N) 시간 복잡도를 갖는다.

  • 검색하고 싶은 문자열 M의 0~i 까지의 부분 문자열 중에서 prefix == suffix 의 가장 긴 길이를 배열로 저장한다.

    • 이때 prefix, suffix 가 부분문자열의 전체가 되어선 안된다.


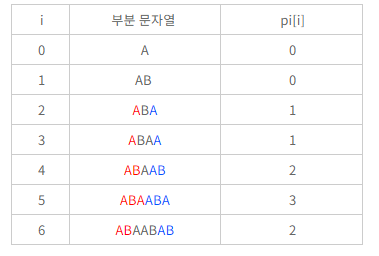
  • 문자열을 검색할 때 일치한 부분 만큼을 인덱스로 삼아 앞서 구한 배열을 참조하여 다음 검색 시작 부분을 suffix 시작 위치로 건너 뛴다.

  • N 을 순회하는 인덱스 i, M 을 순회하는 인덱스를 j 라 할 때, i = j = 6 에서 둘이 불일치한다.
  • 둘이 불일치하므로 pi[j-1] = pi[5] = 2 가 다음번 j 값이 된다.
    • 즉 검색 문자열 M 을 suffix 시작위치로 건너뛰어 다시 검사한다.

  • i = 6, j = 2
  • 둘이 일치하므로 검사를 계속해서 진행한다.
    • i 값과 j 값을 계속해서 1씩 증가

vector<int> makePi(string p){
    int m = (int)p.size(), j=0;
    vector<int> pi(m, 0);
    for(int i = 1; i< m ; i++){
        while(j > 0 && p[i] !=  p[j])
            j = pi[j-1];
        if(p[i] == p[j])
            pi[i] = ++j;
    }
    return pi;
}

vector<int> kmp(string s, string p){
    vector<int> ans;
    auto pi = makePi(p);
    int n = (int)s.size(), m = (int)p.size(), j =0;
    for(int i = 0 ; i < n ; i++){
        while(j>0 && s[i] != p[j])
            j = pi[j-1];
        if(s[i] == p[j]){
            if(j==m-1){
                ans.push_back(i-m+1);
                j = pi[j];
            }else{
                j++;
            }
        }
    }
    return ans;
}

이진 탐색

  • 정렬된 배열에서 타겟을 찾는 검색 알고리즘

  • 배열의 요소들의 범위를 반씩 좁혀가며 타겟을 찾는다.

    • 따라서 O(log n) 시간 복잡도를 갖는다.

  • 정렬된 배열의 길이를 N이라 하면

    • 첫 실행 후에는 N/2 만 남는다.

    • 두 번째 실행 후에는 1/2 * N/2 만 남는다.

    • k 번째 실행 후에는 (1/2)^k * N 만 남는다.

    • 최악의 경우, 탐색이 끝나는 시점에는 한 개만 남게된다.

    • 따라서 (1/2)^k * N ~= 1

    • N ~= 2^k

    • log2_N ~= k

    • 입력한 자료길이 N에 대한 시행횟수 k는 log2_N 이므로 시간 복잡도는 O(logN) 이다.


Lower Bound, Upper Bound

  • 경계값을 찾는 알고리즘

  • Lower Bound 는 정렬된 배열에서 특정 값의 시작 위치를 찾는 알고리즘이다.

  • Upper Bound 는 정렬된 배열에서 특정 값보다 처음으로 큰 값의 시작 위치를 찾는 알고리즘이다.

  • 이진 탐색을 기반으로 수행된다.

    • 시간 복잡도 O(logN)

  • Lower Bound

    • 배열의 중간값이 검색값보다 작으면 left = mid + 1

    • 배열의 중간값이 검색값보다 크거나 같으면 right = mid

    • left >= right 이 되면 반복 종료

    • 이때의 right 값이 lower bound 이다.

def lower_bound(arr, left, right, k):
	while left < right:
		mid = (left + right)//2
		if arr[mid] < k:
			left = mid + 1
		else:
			right = mid

	return right

  • Upper Bound

    • 배열의 중간값이 검색값보다 작거나 같으면 left = mid + 1

    • 배열의 중간값이 검색값보다 크면 right = mid

    • left >= right 이 되면 반복 종료

    • 이때의 right 값이 upper bound 이다.

def upper_bound(arr, left, right, k):
	while left < right:
		mid = (left + right)//2
		if arr[mid] <= k:
			left = mid + 1
		else:
			right = mid
		
	return right

삼진 탐색의 시간 복잡도

  • 입력 배열을 매 시행마다 1/3 등분하기 때문에 O(log3_N) = O(logN) 시간 복잡도를 갖는다.

  • 상수항을 제거하는 Big-O 표기법만 보면 이진 탐색보다 삼진 탐색이 효율적으로 보인다.

    • 그러나 삼진 탐색은 이진 탐색보다 비교횟수 (상수항) 가 많다.

    • 따라서 최악의 경우에 대해서, 실제 비교횟수를 고려하면 이진 탐색이 더 효율적이다.


그리디 알고리즘과 DP

  • 그리디 알고리즘

    • 눈 앞의 이익만을 쫓는 알고리즘

      • 로컬 최적해를 연속해서 찾는 것이 전역 최적해가 된다.

    • 탐욕 선택 속성과 최적 부분 구조를 갖는 문제들이 그리디 알고리즘으로 잘 풀린다.

      • 탐욕 선택 속성 : 앞의 선택이 이후 선택에 영향을 주지 않는다.

      • 최적 부분 구조 : 문제의 최적 해결 방법이 부분 문제에 최적 해결 방법들의 합으로 구성되어 있다.

  • DP

    • 최적 부분 구조와 중복된 하위 문제 특성을 갖는 문제들이 DP 알고리즘으로 잘 풀린다.

      • 중복된 하위 문제

        • 큰 문제를 풀기 위해 동일한 하위 문제들이 발생한다.

        • 따라서 중복된 하위 문제들의 정답을 저장 후, 큰 문제의 결과를 구할 때 사용한다.

  • 두 알고리즘 모두 최적 부분 구조를 갖는다는 공통점이 있다.

  • 그리디 알고리즘은 항상 매 순간에 최적이라고 생각되는 것을 선택하면서 하위 문제들을 푸는데 반해, DP는 하위 문제들을 차례대로 모두 풀이한다.


어떤 경우에 각각의 기법을 적용할 수 있을까?

  • 그리디 알고리즘은 매 순간마다의 로컬 최적해를 구하는 것이 전역 최적해가 될 것임이 예상될때 사용한다.

    • DP 보다 빠르다.

  • DP 는 매 순간마다의 로컬 최적해를 구하는 것이 전역 최적해가 될 것이라는 보장이 없는 경우 사용한다.


출처

시간 복잡도
https://www.youtube.com/watch?v=tTFoClBZutw

공간 복잡도
https://www.youtube.com/watch?v=OnsXVMF9Z1g&t=333s

Big-O를 사용하는 이유
https://softwareengineering.stackexchange.com/questions/99372/why-is-big-o-taught-instead-of-big-theta

O(1) vs O(n)
https://velog.io/@g_c0916/Big-O-%ED%91%9C%EA%B8%B0%EB%B2%95-%EC%8B%9C%EA%B0%84%EB%B3%B5%EC%9E%A1%EB%8F%84

Adjacency List
https://www.geeksforgeeks.org/graph-and-its-representations/

해시 자료구조
https://www.youtube.com/watch?v=ZBu_slSH5Sk

open addressing
https://www.youtube.com/watch?v=Dk57JonwKNk

자바의 해시 충돌 처리
https://d2.naver.com/helloworld/831311

이진 탐색 트리 (1)
https://velog.io/@main_door/%EC%9D%B4%EC%A7%84-%ED%8A%B8%EB%A6%AC%EC%99%80-%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-%ED%8A%B8%EB%A6%AC#%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-%ED%8A%B8%EB%A6%AC%EC%9D%98-%EA%B5%AC%EC%84%B1

이진 탐색 트리 (2)
https://www.youtube.com/watch?v=i57ZGhOVPcI
이중해싱
https://m.blog.naver.com/beaqon/221300416700

힙
건국대학교 김원준 교수님 임베디드 자료구조 수업

BBST
https://www.youtube.com/watch?v=Kuw0f3-E-Hw&t=1s

AVL 트리
https://www.youtube.com/watch?v=syGPNOhsnI4

Red Black 트리
https://www.youtube.com/watch?v=2MdsebfJOyM

2-3-4 트리
https://www.youtube.com/watch?v=ad3tnpLCxYk

insertion sort stability
https://www.baeldung.com/cs/selection-sort-stable

sort algorithm
https://www.youtube.com/watch?v=Du-EHAUE0kM&t=145s

radix sort
https://yabmoons.tistory.com/248

quick sort 최악의 case 개선법
https://guti-coding.tistory.com/158

자바의 정렬
https://codingdog.tistory.com/entry/java%EC%9D%98-arrayssort-%EB%A9%94%EC%84%9C%EB%93%9C%EB%8A%94-%EC%96%B4%EB%96%A4-%EC%A0%95%EB%A0%AC%EC%9D%84-%EC%82%AC%EC%9A%A9%ED%95%A0%EA%B9%8C%EC%9A%94

dual-pivot quick sort (1)
https://www.geeksforgeeks.org/dual-pivot-quicksort/

dual-pivot quick sort (2)
https://www.youtube.com/watch?v=r3a25XPf2A8

dual-pivot quick sort (3)
https://www.youtube.com/watch?v=mI9lBmzzTyQ

Tim sort (1)
https://d2.naver.com/helloworld/0315536

Tim sort (2)
https://www.youtube.com/watch?v=2pjUsuHTqHc

외부 정렬
https://dudri63.github.io/2019/02/03/algo32/

그래프 자료구조
https://www.youtube.com/watch?v=_gIqaC7iLZk

dijkstra time complexity
https://www.baeldung.com/cs/dijkstra-time-complexity

dijkstra 음수 가중치
https://kangworld.tistory.com/76

bellman-ford (1)
https://www.youtube.com/watch?v=0NrlN88D9Fs

bellman-ford (2)
https://great-park.tistory.com/134

floyd-warshall
https://www.youtube.com/watch?v=hw-SvAR3Zqg

A* 알고리즘 (1)
https://www.youtube.com/watch?v=pUZhNMAqLbI

A* 알고리즘 (2)
https://itmining.tistory.com/66

lca 알고리즘 (1)
https://codingdog.tistory.com/entry/%ED%8A%B8%EB%A6%AC%EC%97%90%EC%84%9C-%EC%B5%9C%EB%8B%A8-%EA%B2%BD%EB%A1%9C%EB%A5%BC-%EA%B5%AC%ED%95%98%EA%B8%B0-%EC%9C%84%ED%95%9C-%EB%98%90-%EB%8B%A4%EB%A5%B8-%EB%B0%A9%EB%B2%95

lca 알고리즘 (2)
https://www.crocus.co.kr/660

꼬리재귀
https://joooing.tistory.com/entry/%EC%9E%AC%EA%B7%80-%E2%86%92-%EA%BC%AC%EB%A6%AC-%EC%9E%AC%EA%B7%80-Tail-Recursion

MST
https://www.youtube.com/watch?v=CFZaDJBdEkQ

Union-Find
https://blog.naver.com/ndb796/221230967614

Union-Find 와 Kruskal
https://blog.naver.com/ndb796/221230994142

Synchronized Collections vs Concurrent Collections
https://www.baeldung.com/java-synchronized-collections

LinkedBlockingQueue vs ConcurrentLinkedQueue
https://www.baeldung.com/java-queue-linkedblocking-concurrentlinked

Atomic
https://junhyunny.github.io/information/java/java-atomic/

ConcurrentHashMap
https://blog.hexabrain.net/403#%EC%9E%90%EB%B0%94-8-%EC%9D%B4%ED%9B%84-concurrenthashmap%EC%9D%98-%EB%82%B4%EB%B6%80-%EA%B5%AC%EC%A1%B0

kmp 알고리즘
https://bowbowbow.tistory.com/6

이진 탐색 시간복잡도 증명
https://jwoop.tistory.com/9

lower bound, upper bound
https://yoongrammer.tistory.com/105

profile
Hyun
다음 포스트

운영체제 면접질문 정리

0개의 댓글