Positional Encoding

트랜스포머의 입력은 RNN과 달리 한꺼번에 모든 요소가 들어가기 때문에, 번역, 요약이나 대답을 하는 모델을 만들 때, 토큰의 선후관계나 거리를 유추하는데 어려움이 있습니다. 따라서 각 임베딩 벡터에 모종의 처리를 하여 패턴을 학습하기 수월하게 했는데요. 주로 사용되는 Sinusoidal Positional Encoding의 장점에 대해 알아보겠습니다.

좋은 인코딩을 찾기 위한 시도들

이 부분은 Master Positional Encoding: Part I 을 참고하여 작성하였습니다. 사진 역시 동일한 출처입니다.

0. Fixed positional encoding

positional encoding은 크게 두 종류가 있습니다. fixed positional encoding은
position마다의 positional encoding이 정해져 있는 경우입니다. 즉 1번째 자리는 어느 sequence에서든 같은 positional encoding vector가 들어 있어야 합니다. 앞으로 나올 예시는 모두 fixed positional encoding입니다.

1. Just count:

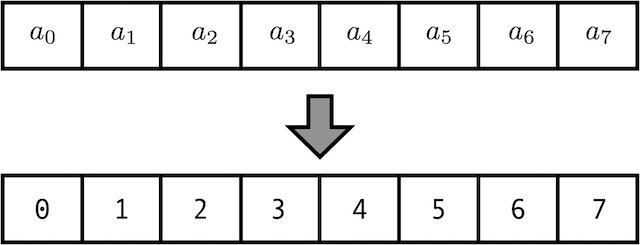
이 방식은 깔끔해 보이지만 치명적인 단점이 있습니다. 숫자가 너무 빨리 커져서 Weight가 갈수록 커지게 되고, gradient vanishing이나 gradient explosion등 학습이 불안정하게 진행될 수 있습니다.

2. Normalize the “just count” guess:

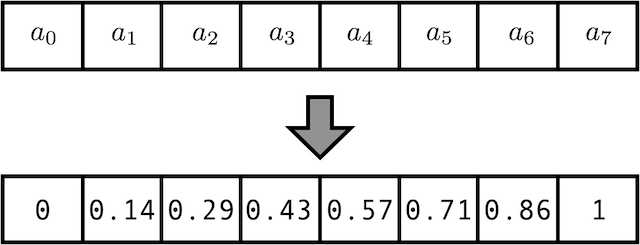
그렇다면 Normalize하면 어떨까요? 1번 방법에서 모든 값은 (max_len-1)로 나눠주면 됩니다. 이제 모든 값은 0에서 1 사이이므로 안정적인 학습이 이뤄질 것 같습니다. 그러나 길이가 가변적이거나, max_len이 다른 데이터셋 끼리의 비교는 힘듭니다. 좋은 fixed positional encoding은 같은 포지션이라면 같은 positional encoding vector를 갖고, 다른 포지션이라면 다른 positional encoding vector를 가져야 하는데, 이 경우 max_len = 13 인 데이터셋에서의 10번째 자리와, max_len = 5인 dataset에서 4번째 자리가 같은 positional encoding vector(0.75)를 가지게 되면서 바람직한 인코딩이 아니게 됩니다.

따라서 이 방법은 어떤 max_len을 갖는 데이터셋에든 일반적으로 적용할 수는 없습니다.

3. Just count! but using binary instead of decimal:

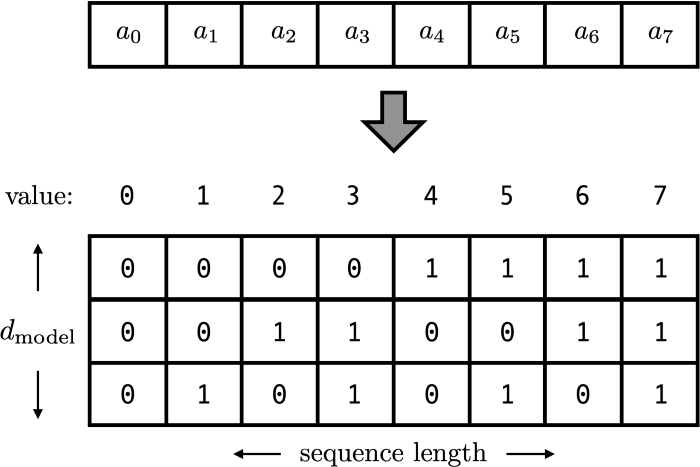
방법 1, 2까지 positional encoding vector라고 부른 것들은 사실 1x1 사이즈의 스칼라였습니다. 이제부터는 각 position에 해당하는 d_model 차원 벡터가 되었습니다. 각 열벡터가 하나의 positional encoding vector가 되고, 이진수로 현재의 위치를 표현하게 됩니다. 2^d 보다 작은 max_len을 갖는 dataset은 모두 표현할 수 있고, 가변적인 길이에도 같은 위치라면 같은 값이 할당되기에 좋은 성질을 갖습니다. 값도 0과 1 사이라서 안정적인 학습에도 바람직해 보입니다. (평균이 0이 되길 원한다면 0과 1 대신 -1과 1을 갖게 해도 상관없습니다)

그러나 이 방법도 본질적인 문제가 있습니다.

Our binary vectors come from a discrete function, and not a discretization of a continuous function.

이산적 함수의 출력이라서 문제가 된다는 것은 무슨 의미일까요?

연속함수인 y = x의 출력 $(0,\; 0.33,\; 0.66,\; 1.00)$ (방법2)-파랑과
이산함수의 이진수 출력 $((0,0), (0,1), (1,0), (1,1))$ (방법3)-검정을 비교해보겠습니다.

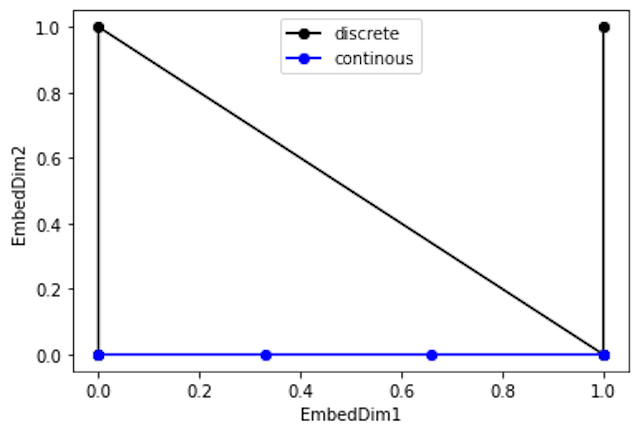
파랑 선은 점 사이 간격이 일정한 것을 볼 수 있지만, 검은 점들 간 거리는

가 됩니다. 같은 거리를 상정 $(D(0\rightarrow1)\;=\; D(1\rightarrow2)$ 이 되기를 원함$)$ 했음에도 모델은 다른 거리로 판단하게 되는 것$(D(0\rightarrow1)\;\neq\; D(1\rightarrow2))$입니다. 이는 고차원으로 갈수록 더욱 문제가 되어 binary count를 사용하는 것은 바람직하지 않습니다.

따라서, 다음으로 해결해야 할 과제는 점들이 등간격으로(혹은 거리로 써 먹을 수 있는 값을 뽑아낼 수 있는)배열된 부드러운 곡선을 찾는것, 다시 말하자면
embedding manifold를 찾는 것입니다.

So with pictures, we want a function that connects the dots in a smooth way that looks natural. For anyone who has studied geometry, what we are really doing is finding an embedding manifold.

4. Use a continuous binary vector:

이제 연속적이고 부드러운 함수를 찾아야 합니다.
0과 1을 부드럽게 움직이는 함수는 진동, 주기성과 관계가 있고, 모두 삼각함수로 표현할 수 있습니다. Sine을 이용해 보겠습니다.

Sine은 진동수(얼마나 빨리 회전하여 한 바퀴 도는지)와 진폭(한 바퀴 돌 때 얼마나 변하는지)을 조절할 수 있습니다. (이 경우, 위상차는0으로 고정) -1부터 1까지 진동하는 것은 이미 Normalize가 된 것이므로 진폭은 손대지 않고 진동수만의 차이를 주어 그 sine들의 출력으로 positional encoding을 시도해 보겠습니다.

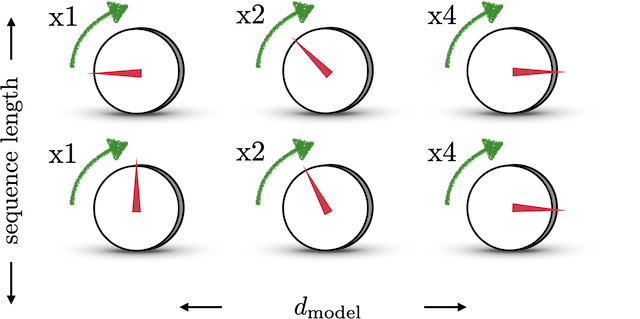
이제부터는 positional encoding vector를 행벡터로 표현하겠습니다. sine들은 다른 속도로 도는 다이얼로 묘사되어 있고, $90\degree$를 이동하는데 몇 time step이 걸리는지 $\times N$ 으로 표시했습니다.
오른쪽으로 한 칸씩 가면 같은 각을 진행하는데 걸리는 시간이 두배가 됩니다. 즉 절반의 진동수로 도는 구조입니다. 이 경우, 가장 느린 쪽이 한 바퀴를 돌기 전까지의 사인값의 순서쌍이 모두 다르게 됩니다. (반 바퀴째를 도는 순간을 제외하면) 이를 그림으로 나타내면 다음과 같습니다.

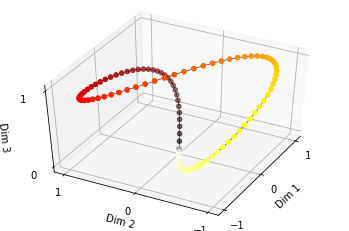
The colors indicate the absolute position that that coordinate represents. Frequencies are omega=pi/2, pi/4, pi/8 for dimensions 1, 2 and 3 respectively.

$(0,\; 0,\; 0)$에서 시작해서 Dim 3 이 가장 느리게 진동하고, Dim 2는 그 두배, Dim 1은 Dim 2의 두배로 진동하는 상황의 사인값의 순서쌍을 공간에 그렸습니다. 스텝사이 간격이 일정한, 부드러운 함수가 된 것을 볼 수 있습니다.

하지만 아직 고쳐야 할 문제점이 두개 남아있습니다.

5. Final answer

문제점1. 직전그림을 보면 DIm 3의 사인함수가 반바퀴 돌았을 때, 원래의 위치로 돌아옵니다. 이 경우 1번째 스텝과 반 바퀴를 돌았을 때의 스텝의 거리가 매우 가까워져 모델 학습에 영향을 미칩니다.

문제점2. 스텝 차이에 의존하는 변환이 존재하지 않습니다.

문제점 1의 경우 각 sine들의 주기가 가장 느린 sine 주기의 $2^n$배
이기 때문에 생기는 문제이고,
문제점 2는 $(x+\Delta x)\;=\;T(\Delta x)x$를 만족하는, $\Delta x$에만 의존하는 $T(\Delta x)$ 가 존재하지 않는다는 의미입니다.

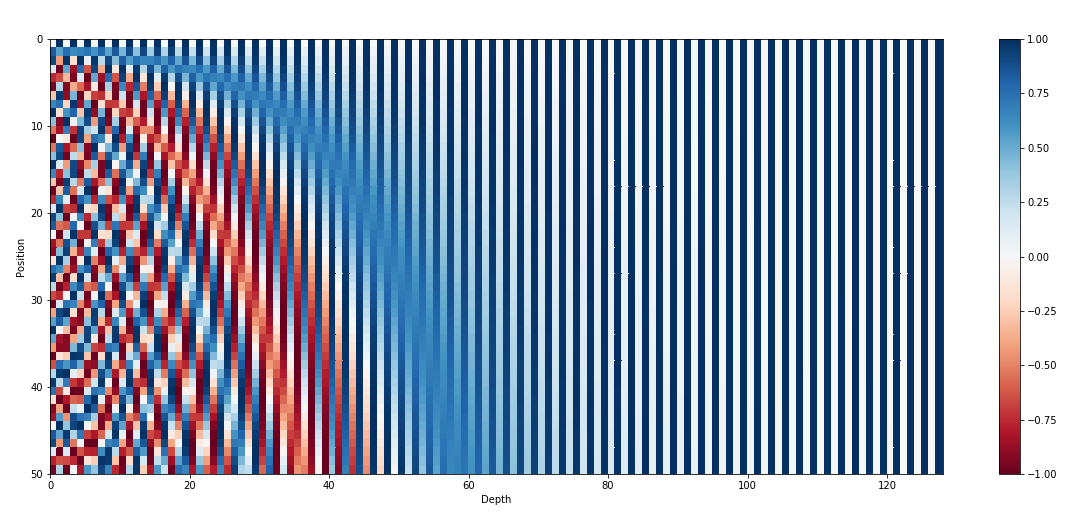
Sinusoidal Encoding

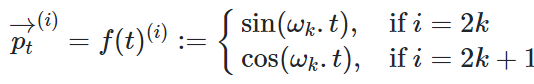
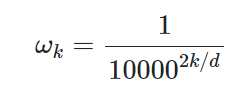
Sinusoidal Encoding의 식은 위와 같이 주어집니다. 주기는 $\omega$에 반비례하므로 $10000^{2k/d}$에 비례하게 되고, 문제점 1은 발생하지 않습니다. 또한 cosine을 사용하게 되면,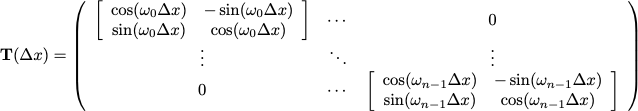
Translation operator가 위와 같이 정의되므로 문제점 2또한 해결됩니다.

보너스 성질
트랜스포머에서는 내적이 매우 많이 사용됩니다. 이 때, 두 벡터 사이의 내적을 구한다면 $\\(x+\Delta x)^t x\;=\;(T(\Delta x)x)^tx\;=\;x^tT^t(\Delta x)x$입니다. $T^t(\Delta x)$는 반대 방향으로의 회전변환을 의미하므로, 결국 회전변환을 적용한 벡터 $T^t(\Delta x)x$와 $x$의 내적이 되어 차이 $\Delta x$가 커질수록 내적이 작아지는 경향성을 볼 수 있습니다.

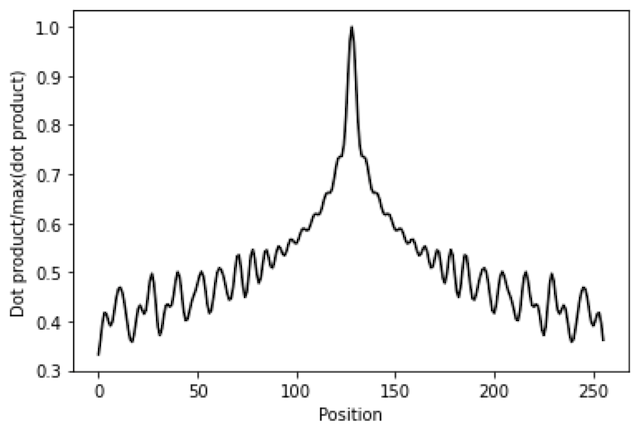
따라서 내적을 사용하는 트랜스포머 구조에서 포지션 간 간격에 대한 패턴을 학습하기 좋습니다

결론

Sinusoidal Positional Encoding은 부드러운 함수에서 추출되고, 좋은 성질이 있어서 포지션 끼리 가까우면 내적이 크고, 멀면 내적이 작아져서 내적으로부터 거리관계를 대략 유추해낼 수 있습니다. 또한 max_len이 다양한 dataset에도 동일하게 적용가능합니다.

Sinusoidal Positional Encoding은 이처럼 많은 장점이 있어 자주 사용됩니다