Conv1D는 오디오, 센서와 같은 1차원 시계열 데이터를 위한 1D Convolution 이다. 여기서 말하는 1D는 데이터 차원을 의미하는 것이 아나라 한 방향으로 이동하면서 연산을 수행한다는 의미이다. 즉, 다차원 시계열 데이터(Multivariate Time Series Data)도 1D convolution을 수행 한다. 입력신호 에 대한 Conv1D 의 출력신호 은 다음과 같이 표현된다.
여기서, 은 배치사이즈, 는 채널수, 은 신호의 길이를 나타낸다. 이때, 입력신호와 출력신호의 모양은 다음과 같다.
수식만으로는 어떻게 동작되는지 이해하기 어렵다. 그림과 함께 하나씩 이해해 보자
전체적인 구조
4개의 채널과 17개 포인트로 구성된 입력데이터를 3개의 채널로 변화해 보자. 이해를 쉽게하기 위해 배치는 1로 가정하고, 바이어스는 없다고 가정한다. 이때, window(time_step)=7 이고 stride=1로 한다. 그러면 입력 데이터의 형태는 1x4x17의 형태를 가질 것이고 출력은 1x3x11의 현태를 가지게 되고, 입력 채널이 4이고, 윈도우가 7이기 때문에 커널은 4x7의 형태를 가지게 된다. 출력은 3 채널을 가져야 하기 때문에 4x7형태의 커널은 3개 필요하다. 아래 그림은 이를 도식화 한 것이다.
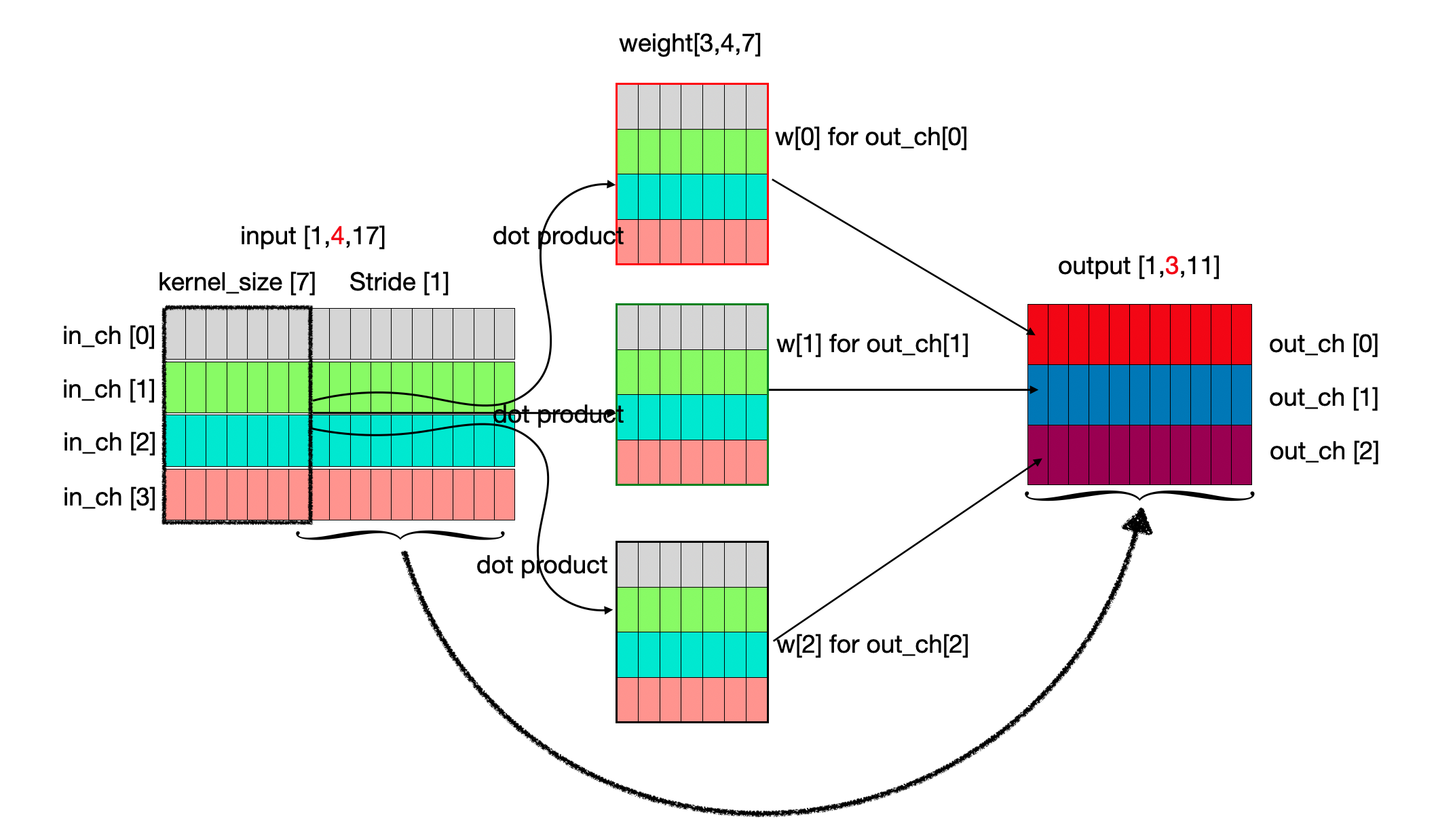
첫번째 입력 데이터에서 시작위치에서 4x7의 데이터를 선택해서 각각의 출력 데이터를 위한 커널과 dot product를 수행하면 출력 채널별로 하나의 숫자가 나오고 이것을 출력 데이터 첫번채 열에 추가한다. 다음으로 입력 신호에서 1 time step(stride=1) 을 이동해서 4x7 데이터를 선택하고 3개의 커널과 dot product을 수행하고 출력 데이터의 2번째 열에 추가한다. 이렇게 계속 반복하면 출력데이터는 1x3x7 형태를 가지게 된다. 입력, 출력, 커널의 변화에 따라 어떻게 달라지는지를 알아보기로 하자.
No Effect
입력, 출력, 커널의 변화를 살펴보기 위해 이를 좀 더 단순화 해서 살펴보자. 가장 단순한 형태로 입력 채널은 1차원, 출력 채널은 1 커널 사이즈는 1로 가정해보자. 입력 데이터는 1,2,3,4,5로 구성되고 커널의 초기값은 0.2로 가정하자. 커널은 하나씩 이동하면서 입력신호와 곱해서 출력을 만든다.
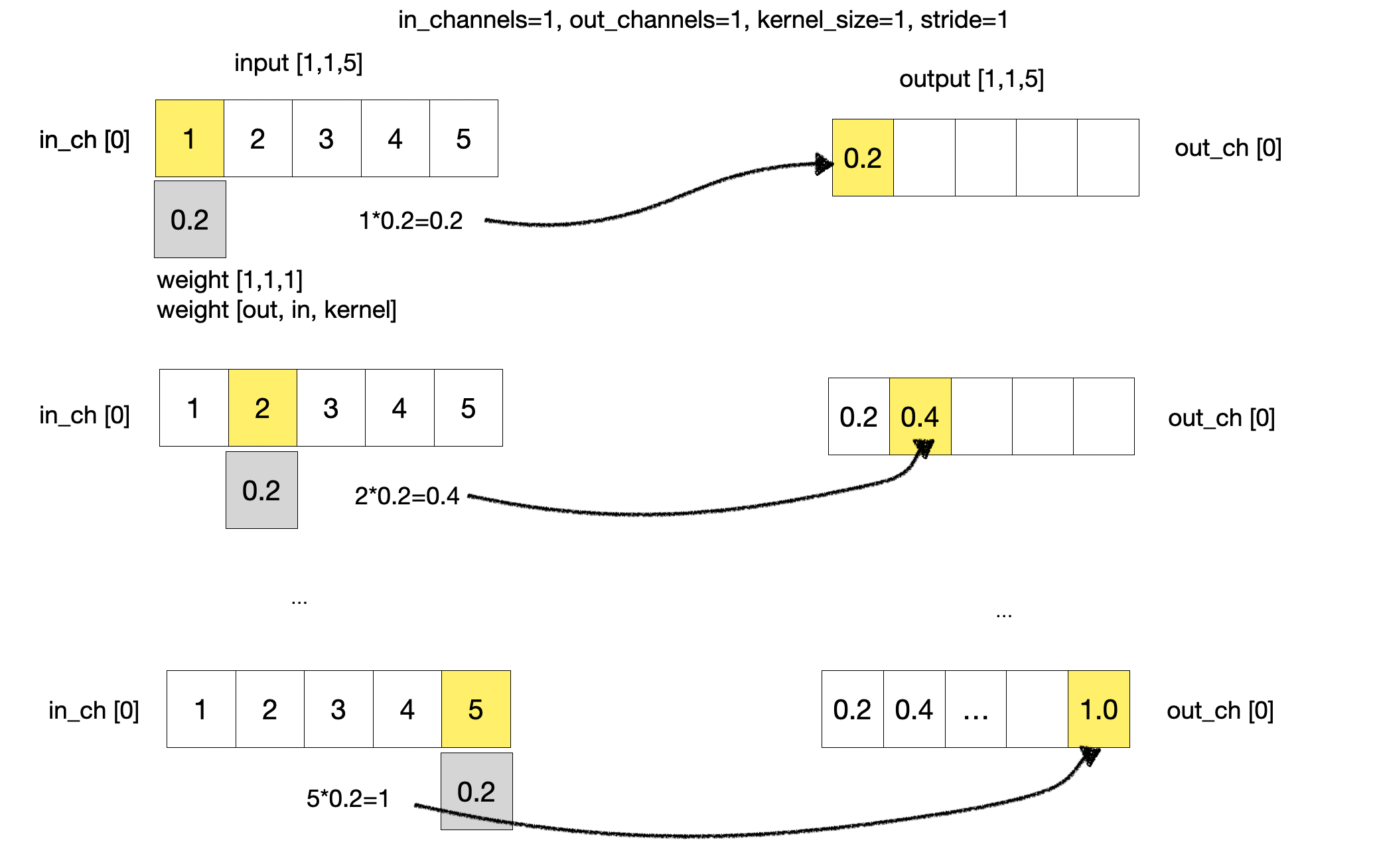
Window(time_step, kernel) Effect
이제 윈도우 사이즈를 1에서 2로 변경해서 어떤 변화가 있는지 살펴보자. 윈도우 사이즈가 2로 변경되었기 때문에 커널과 dot product연산을 위해서는 커널 사이즈도 2로 변경되어야 한다. 이것은 출력 데이터의 형태를 변화시킨다. 이제 입력데이터 1x2와 커널 데이터 1x2의 dot product가 하나의 출력을 생성한다. 순차적인 연산은 동일하게 진행된다.
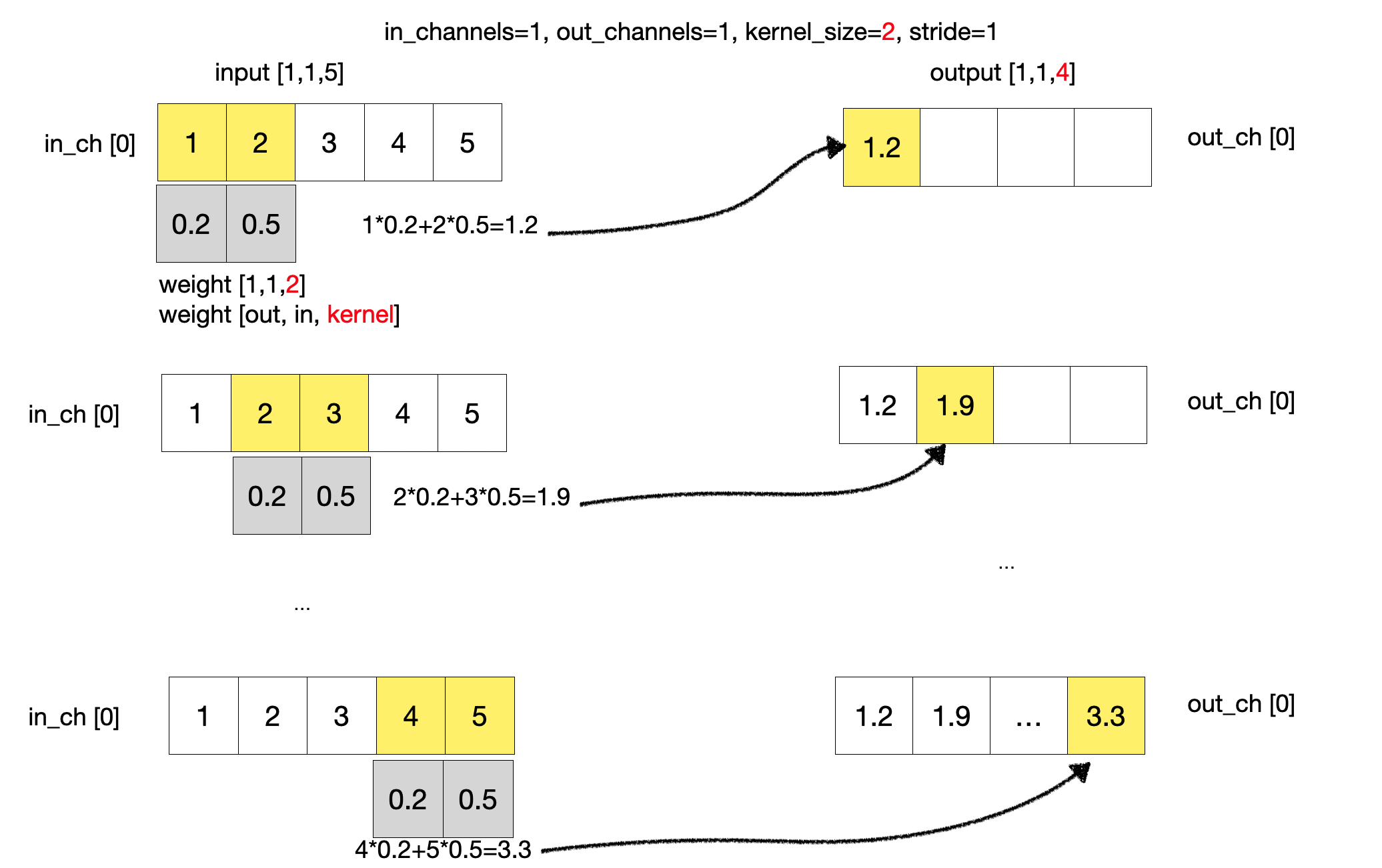
Output Effect
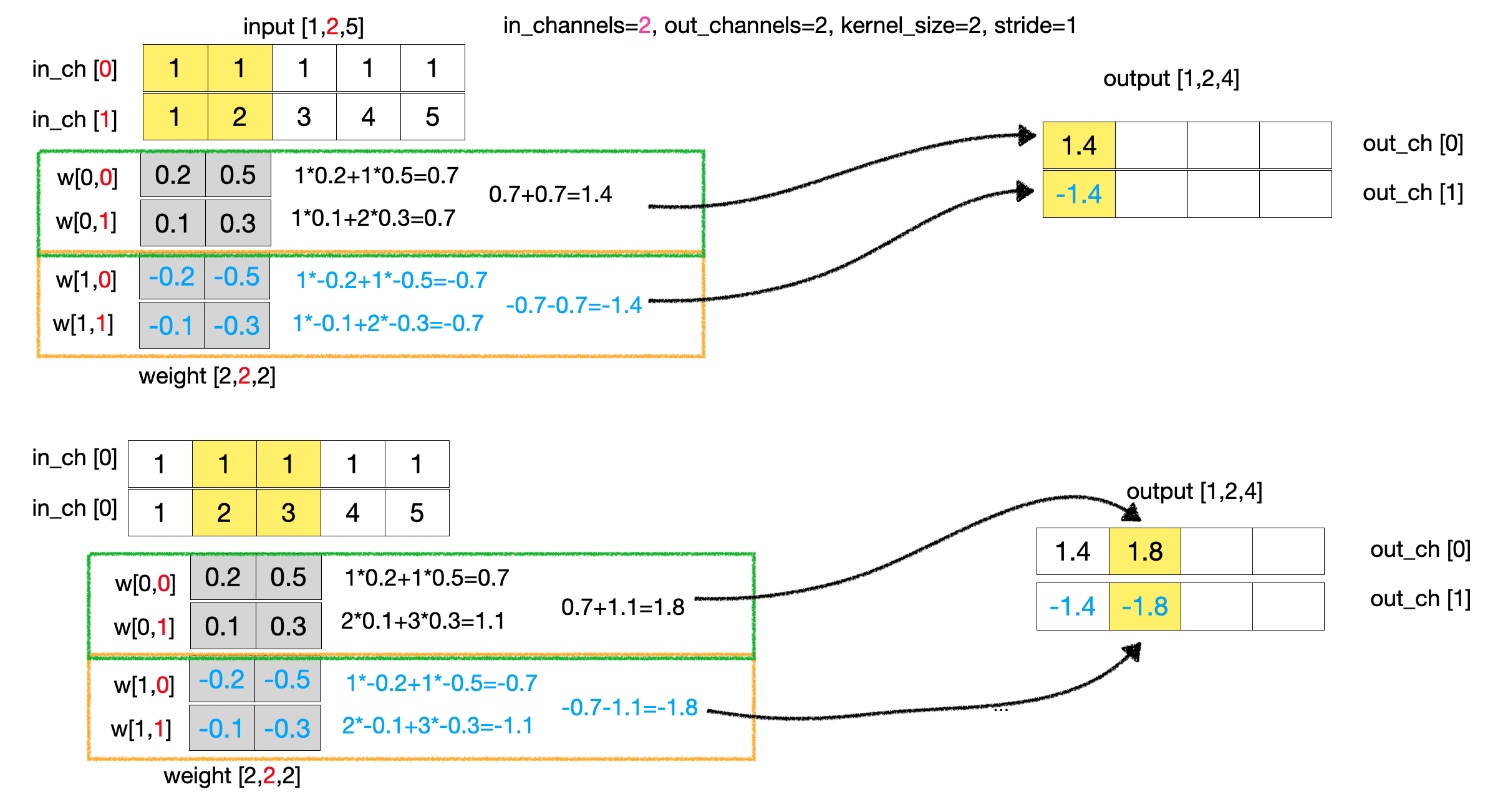
이제 출력데이터를 2차원으로 늘려보자. 출력 데이터가 2차원으로 확장되었기 때문에 커널도 2차원으로 확장되어야 한다. 따라서, 출력 데이터의 형태는 1x2x4로 변경된다. 하지만, 입력 채널은 여전히 1차원이고, 커널은 2차원이 되어야 하기 때문에 입력데이터는 커널의 각 차원과 한번씩 연산을 수행하여 출력 채널을 생성한다.
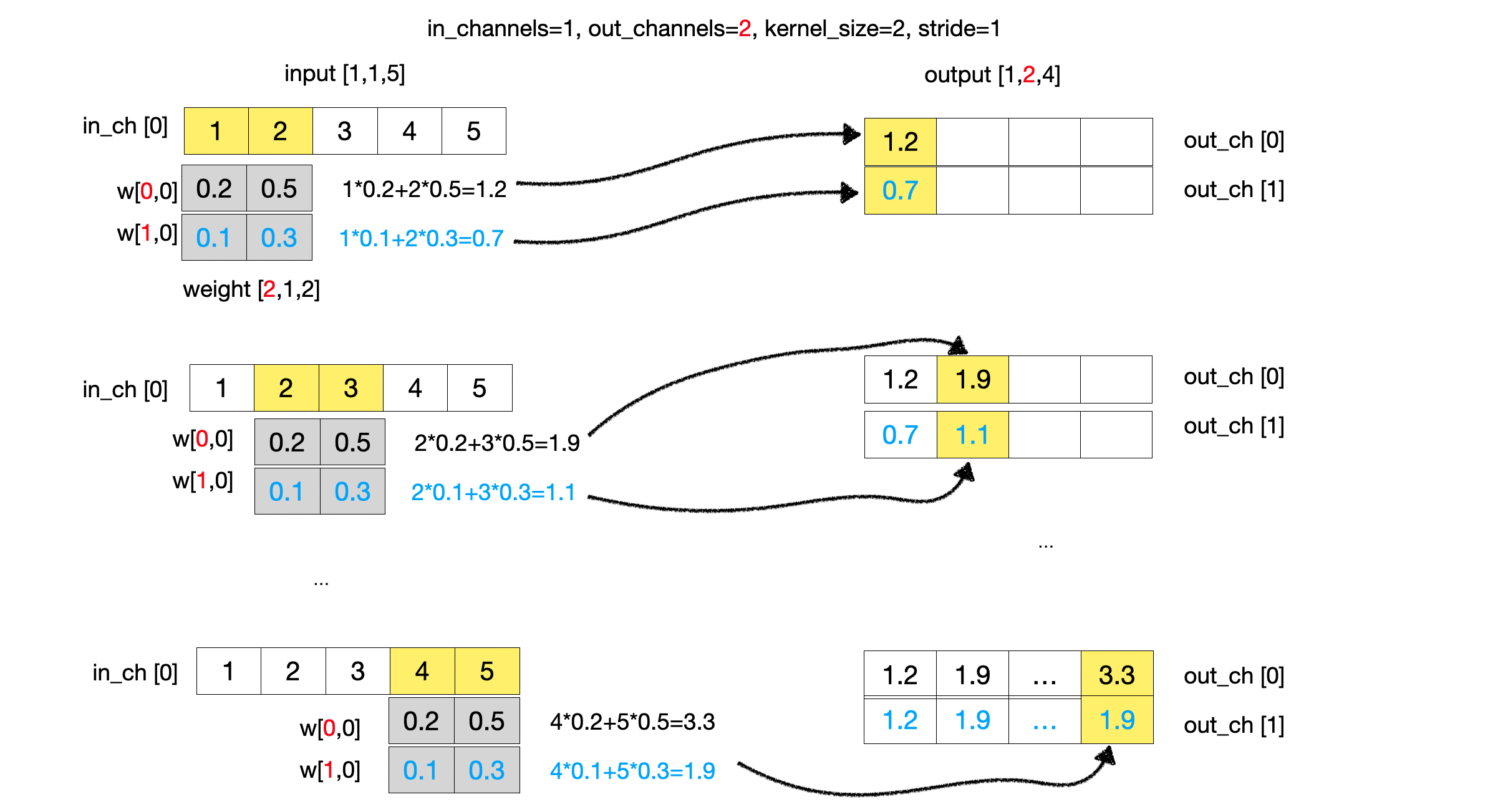
Input Effect
입력 채널이 변화되면 어떤 영향을 미칠까를 알아보기 위해 입력채널을 2로 변경해보자. 입력데이터의 채널수의 변경은 출력 데이터 형태에 어떠한 영향도 미치지 않는다. 하지만, 커널의 채널수에 영향을 미친다. 입력 데이터가 2 차원이기 때문에 각각의 커널은 2차원 이 되어야 한다.