3D representations [CS479]
https://mhsung.github.io/kaist-cs479-fall-2023/
3D representation 1~3강 요약
How to represent 3D objects?
- Voxels
- multi-view
- pointcloud
- mesh
- implicit function
1. Voxels (3D grid)

Voxel은 마인크래프트 박스로 object를 표현한다고 생각하면 된다. 물체의 2D surface를 표현하면 3D object가 어떻게 생겼는지 알 수 있으므로 각 voxel은 표면에 존재할 경우 1, 아니라면 0의 값을 갖는다.
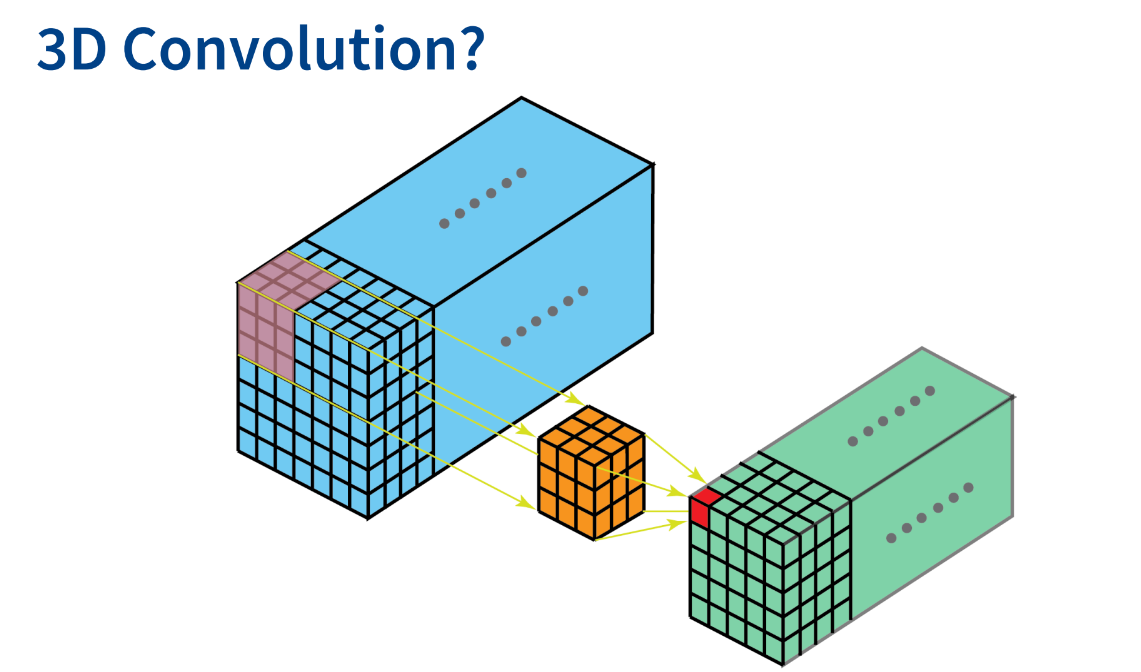
3D CNNs
- 단점
해상도가 높아질수록 대부분의 voxel은 비어있게 되어 3D convolution 시 computation 낭비가 크다. 막대한 양의 memory와 computation time이 필요하다.
- 해결 시도
adaptive data structure

SparseConvNet

2. Multi-View Images
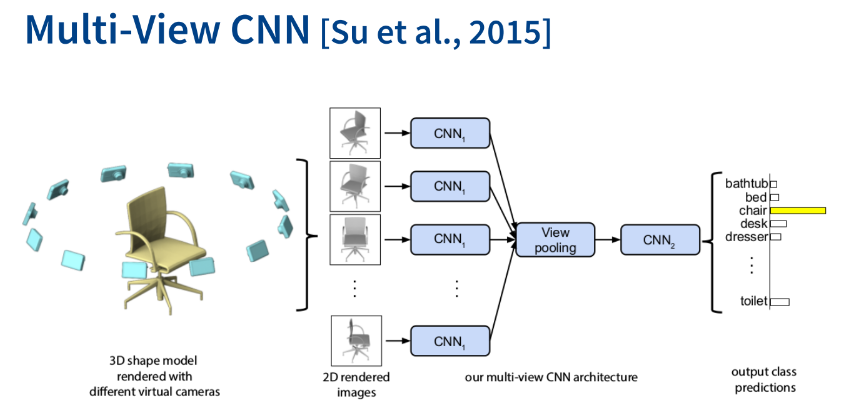
computer graphics를 활용해 3D shape을 다양한 위치에서 본 2D rendered images를 만들고, 이를 2D CNN으로 processing하여 합치는 방법이다.
- 장단점
(+)물체의 appearance 정보(color, texture, material)를 잘 처리한다.
(-)정확도를 높이기 위해서는 많은 이미지가 필요, 이에 따른 memory와 time 문제
(-)기하학적 정보를 처리하기 어렵다.
3. Point Cloud
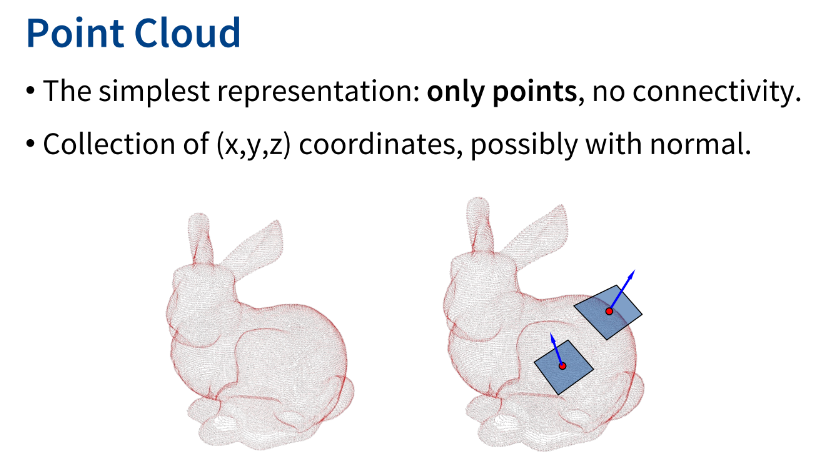
(x,y,z)의 점만으로 표현하는 방법이다. 추가적으로 color 정보 / normal vector 등을 가질 수 있다. 대부분의 3D scanning device(LiDAR 등)는 point cloud를 만들어내게 된다.
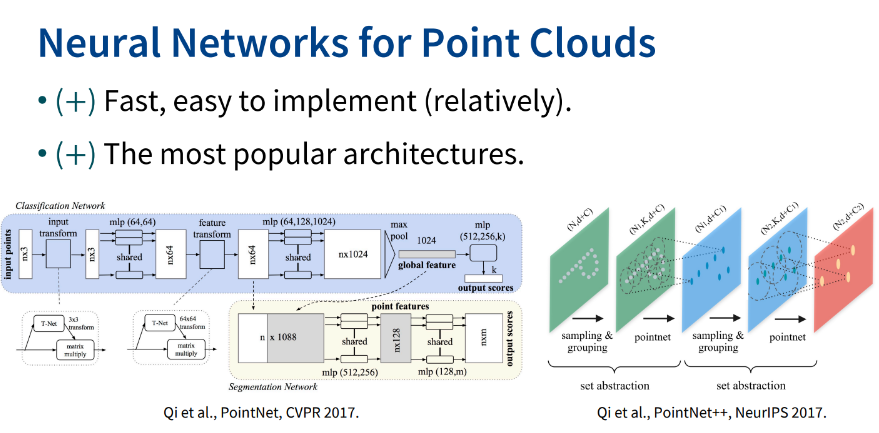
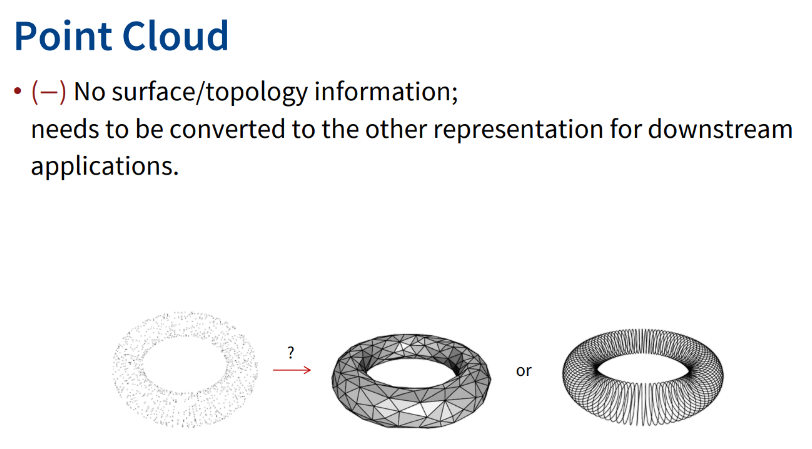

(-) irregular structure라서 convolution을 적용할 수 없다.
4. Polygon Mesh
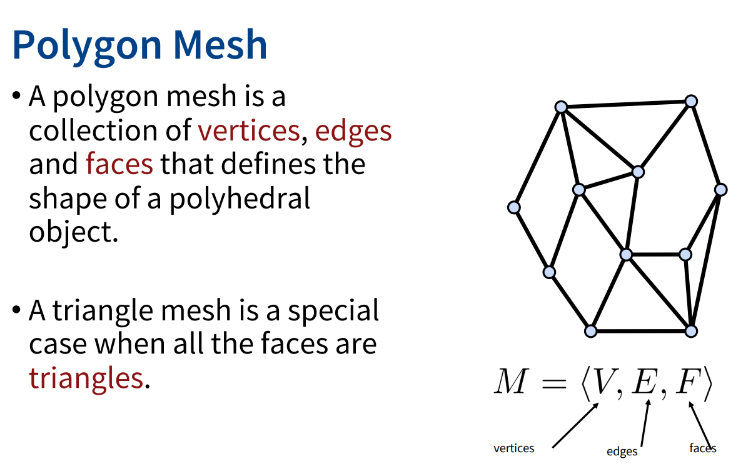
vertices(점) + edges(선), faces(면)
- 장단점
(+) rendering, texture, deformation/manipulation, simulation 등 적용하기 쉽다.
(-) irregular structure라서 convolution을 적용할 수 없다.
(-) Valid mesh를 만들기 어렵다.
3D representation 비교
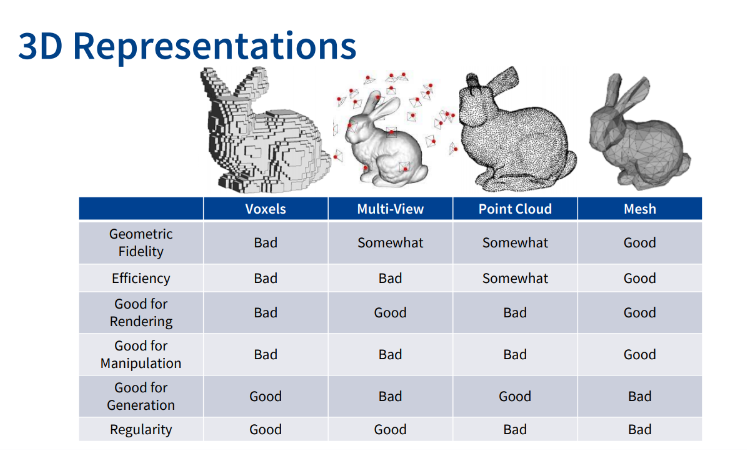
5. Implicit representation
3D shape을 function으로 표현한다. 어떤 (x,y,z)를 input으로 넣으면 해당 point가 object의 내부에 있는지, 외부에 있는지를 output으로 알 수 있다.
Convertion

Voxel -> Mesh
2D marching cubes
discrete space에서 모든 point x에 대해
f(x)<0 : inside
f(x)>0 : outside
를 계산한다.
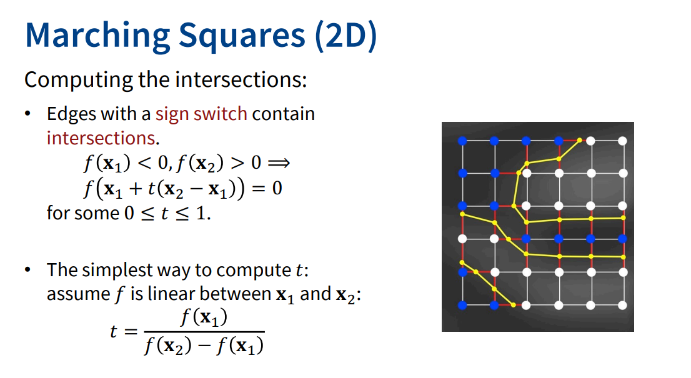
부호가 변하는 edge는 intersection이 존재하므로 이러한 edge에 대해서만 intersection을 찾는다. f가 x1~x2까지 linear하다고 가정하면 t를 구할 수 있다.
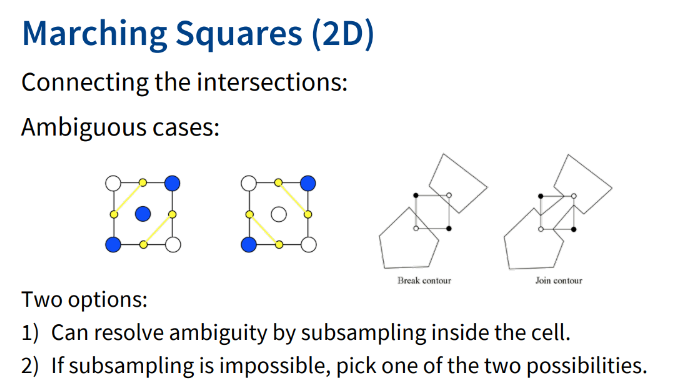
위와 같이 2가지 case 중에서 정답을 알려면 subsampling이 필요한 경우가 있다.
3D marching cubes
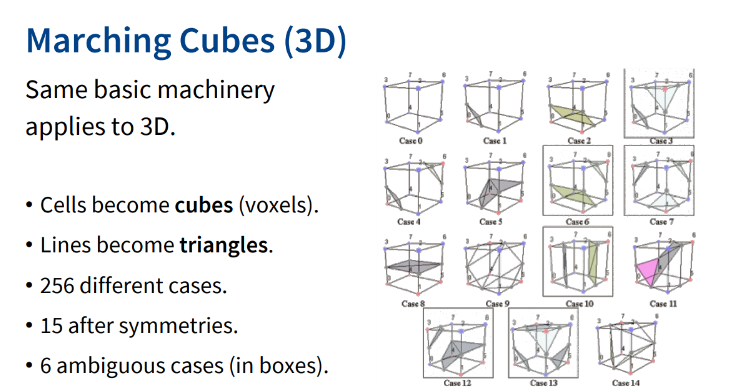
- 장단점
(+) fast, parallelizable(GPU)
(+) simple to implement
(+) virtually parameter free (only resolution)
(-) cannot express sharp edges
Marching Tetrahedra
: cube 대신 tetrahedra(사면체)를 사용한다. marching cube와 달리 ambiguous cases가 없다는 장점이 있다.
Point cloud -> Implicit function
point cloud에서 implicit function으로 변환하기 위해서는 surface normal information이 필수적이다.

point cloud에서 어떤 point의 surface normal을 예측하려면? 주변 점들까지 포함해서(local linear surface라고 가정하고) 가장 맞는 normal plane을 찾는다.
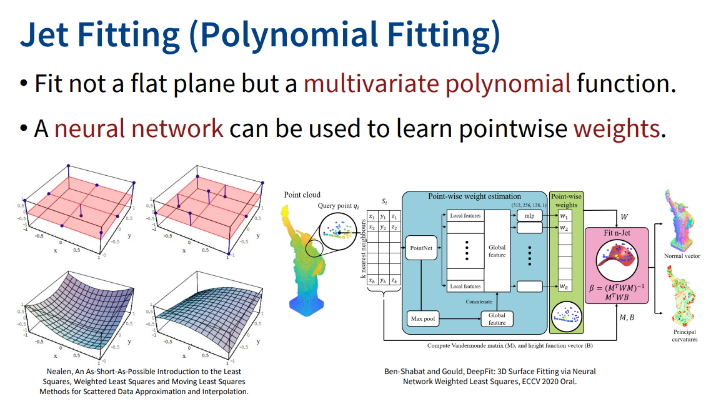
평면이 아닌 multivariate polynomial function(e.g. 구의 일부분)을 fitting하는 방법이다. 이때 polynomial function의 weight를 예측하기 위해 nerual network를 사용하는 방법이 있다고 한다.

signed distance function은 surface와의 거리를 나타낸다. 예를 들어,
에서 (6,0)은 surface에서 거리 이다. 마찬가지로 (0,0)도 이 된다.
point cloud에서 signed distance function을 만들기 위해 여러 방법이 있다. moving least squares, radial basis function, poisson surface reconstruction ... etc.
1. Simplest method

임의의 점 x에서 거리를 구하기 위해 point cloud에서 가장 가까운 점 p를 찾고, 여기서의 tangent plane과의 거리를 구한다.
2. Moving least squares
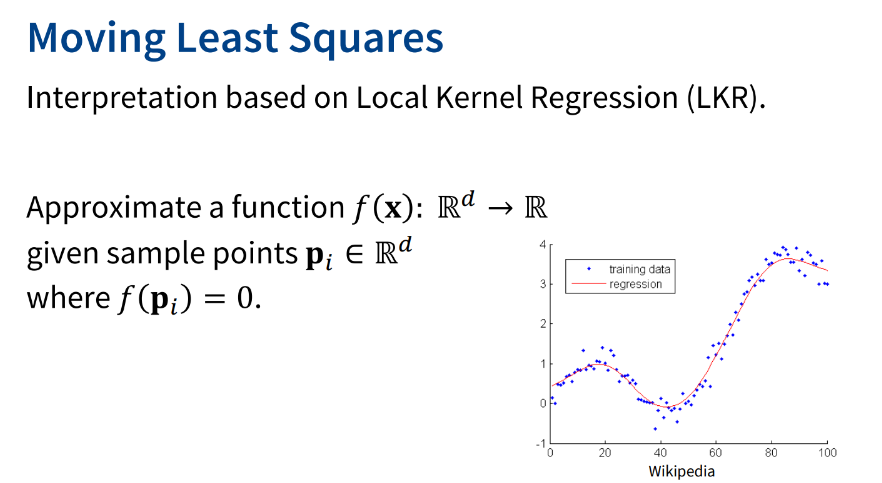
를 만족하는 sample points 를 여러 개 찾고, 이를 통해 를 approximate한다.

0이 되는 점 에 대해 가까운 query point x로 first order Taylor series로 approximate된 다항함수를 구한다. 좌변과 우변의 차이를 최소화하고자 loss를 다음과 같이 구하게 된다.

지금 우리는 query point x를 함수에 넣었을 때의 distance인 y를 구하고자 하고 있다.
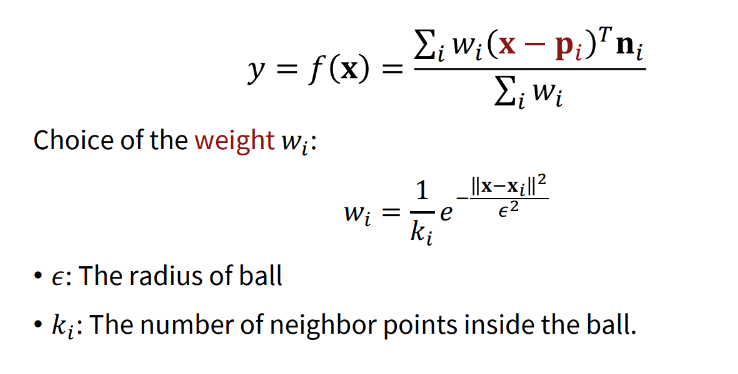
결과적으로 query point x와 pointcloud의 모든 점에 대한 일종의 weighted sum을 구하게 된다. 이때 각 pointcloud 에 대한 weight 를, 위와 같이 query point 가 pointcloud 위의 에서 멀어질수록 weight가 작아지도록 정의했다.
- 장단점
(+) fast & easy to implement
(-) local region에 대해서만 approximation을 진행한다.
(-) weight function을 어떻게 정하는지에 따라 민감하다.
Poisson surface reconstruction
implicit function의 gradient == surface normal vector
(e.g. 3x+4y+5z=0의 gradient = norm 3,4,5)
그렇다면 f를 derivative 로 찾아보자.



V가 integrable 하지 않을 수 있으므로 이를 계산하는 대신 를 최소화하는 f인 를 찾는다.
[오일러-라그랑주 방정식]

라그랑주 방정식에 의해 다변수함수 L에 대한 적분의 최소 or 최대가 되는 점(해)은 두번째 식의 PDE를 풀면 된다. (미분해서 증명 가능)
이를 활용해, 1D에서는 를 최소화하는 를 찾는 과정은 다음과 같다.

[포아송 방정식]

f의 laplacian(2차 도함수) = V의 divergance 꼴을 포아송 방정식이라고 한다.
우리가 풀어야할 식도 이러한 형태이다. 1D에서는 f''=g'이다.

: n개의 점을 sampling
Discrete에서는 각 x_i를 function에 넣은 vector f로 f를 근사할 수 있다. 마찬가지로 discrete first derivate는 matrix A로 근사할 수 있다.

마찬가지로 discrete second derivate는 L로 근사할 수 있다.

다시 돌아와서, 해결해야 되는 poisson eq을 Lf=Ag로 표현할 수 있다.
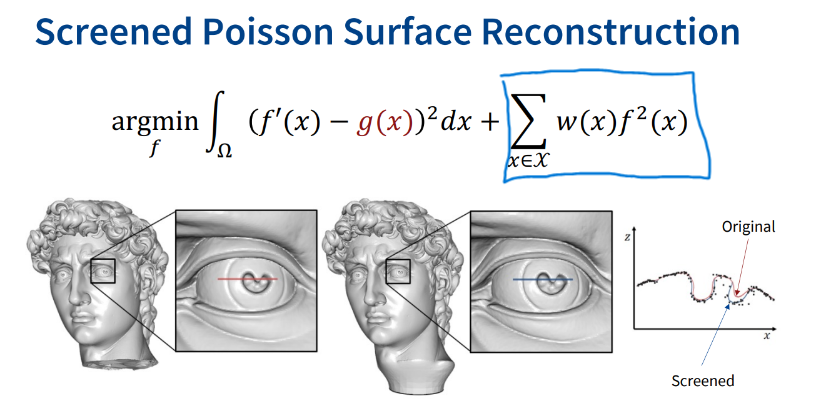
추가적으로 최소화해야 되는 값에 weight에 대한 regularization term(screened의 의미)도 추가해서 궁극적으로 surface function f를 찾는다.

- 단점
(-) 정확하고 연속적인 surface normal이 필요하다.
(-) point cloud 자체가 dense해야 한다.
(-) noise, outlier에 영향을 많이 받는다.
