[Review] 2D Gaussian Splatting for Geometrically Accurate Radiance Fields (+ Viewer 구현)
3D AI
- figure: TSDF reconstructed Mesh from 2D GS, made by hwan
실사용이 가능한 수준의 mesh export 가 가능한 2D Gaussian Splatting for Geometrically Accurate Radiance Fields 를 리뷰해보자!
본격적인 리뷰에 앞서 2D GS 로 직접 만들어본 NeRFBlender dataset lego scene 의 놀라운 모습을 공유한다.
Recap) Radiance Fields 의 Mesh Recon 의 어려움
이전 블로그 글,
를 통해 NeRF 및 Radiance Fields 기술이 아직은 실사용에 어려운 단계라고 공유했었다.
특히 3D GS 의 경우, scene 자체의 게임/그래픽스/애니메이션 엔진으로의 이식 자체는 NeRF 보다 유리하지만 태생이 pointcloud 의 변형에 가까운 3D GS 의 특성상 mesh 로 만드는 것은 오히려 NeRF 보다도 더 어렵다고 했었는데...
이번 SIGGRAPH'24 에 공개된 논문 중 '2D Gaussian Splatting for Geometrically Accurate Radiance Fields' 는 Splatting 기반 연구로써 실제로 사용할 수 있을만한 품질을 보여주고 있어 오랜만에 논문을 리뷰하려 한다.
1. Preliminary
1.1. 3D Gaussian Splatting

3D Gaussian Splatting 이란 anistropic & explicit 한 3D Gaussian 의 집합으로 3D Scene 을 reconstruction 하는 기술이다.
3D GS 원저자들은 학습의 용이성을 위해 3D Gaussians 의 covariance matrix 를 Gaussian 의 Rotation Matrix 과 Scale matrix 을 통해, 공간 위의 어떤 점 에 대한 density function 을 다음과 같이 정의하였다.
3D GS 는 정의상 dense point cloud reconstruction 과도 비슷하지만,
- novel view synthesis 를 위해 공간을 explixit radiance fields 로 재구성하며
- sparsity 를 해결하기 위해 특정 iteration 마다 differentiable 3D GS 의 derivative 를 이용해 densification & removal 하는 refinement 전략을 채택하였다.
이같은 explicit representation 으로 얻게 되는 여러가지 장점이 있는데,
- 빠르다
MLP 에게 query 해서 정보를 얻어야하는 NeRF 와 다르게 (implicit) 3D GS 는 3D Gaussians 의 정보를 explicit 하게 가지고 있으므로, MLP query 없이 scene 을 굉장히 빨리 그릴 수 있다 (100fps 이상). - 게임/그래픽스 엔진으로의 이식 용이성
3D GS의 rasterization 만 구현하면 되므로 게임 엔진으로의 이식에도 훨씬 유리하다. 엔진 뿐만 아니라 web viewer 등도 NeRF 대비 구현하기 훨씬 편리하다. (cf. SuperSplat) - 편집의 용이성
학습된 3D GS scene 에서 특정 floater 만 선택해 지우거나, scene 의 일부분만 지우고 & 남기거나, 다른 3D GS scene 과 병합하여 한 합치는 등의 편집 용이성이 MLP 를 사용하는 NeRF 대비 훨씬 뛰어나다.
1.2. Surface Reconstruction Problem in 3D GS
상기한 3D GS 의 여러 장점이 있지만, 알려진 3D GS 의 가장 큰 단점 중 하나는 surface reconstruction 이 어렵다 는 점이다.
2D GS 에서는 다음 4가지 근거를 통해 3D GS 에서 surface reconstruction 이 어려운 이유를 자세하게 서술하고 있다.
-
Thin Surface 를 배우기 어렵다.
three-dimensional scale 을 배우는 3D GS 의 volumetric radiance representation 은 thin surface 를 표현하기 어렵다. -
Surface Normal 을 배우지 않는다.
surface normal 이 없어 high-quality surface 를 reconstruction 할 수 없다. (INN 에서는 SDF 등으로 이 단점을 해결한다) -
Multi-View Consistency 가 부족하다.
3D GS 의 rasterization 은 각기 다른 viewpoint 에서 다양한 2D intersection surface 가 발생하는 문제가 생긴다. i.e., Artifacts!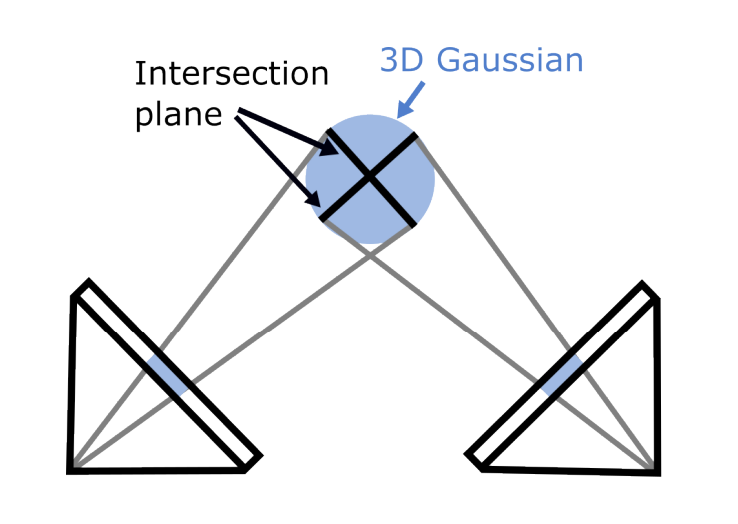
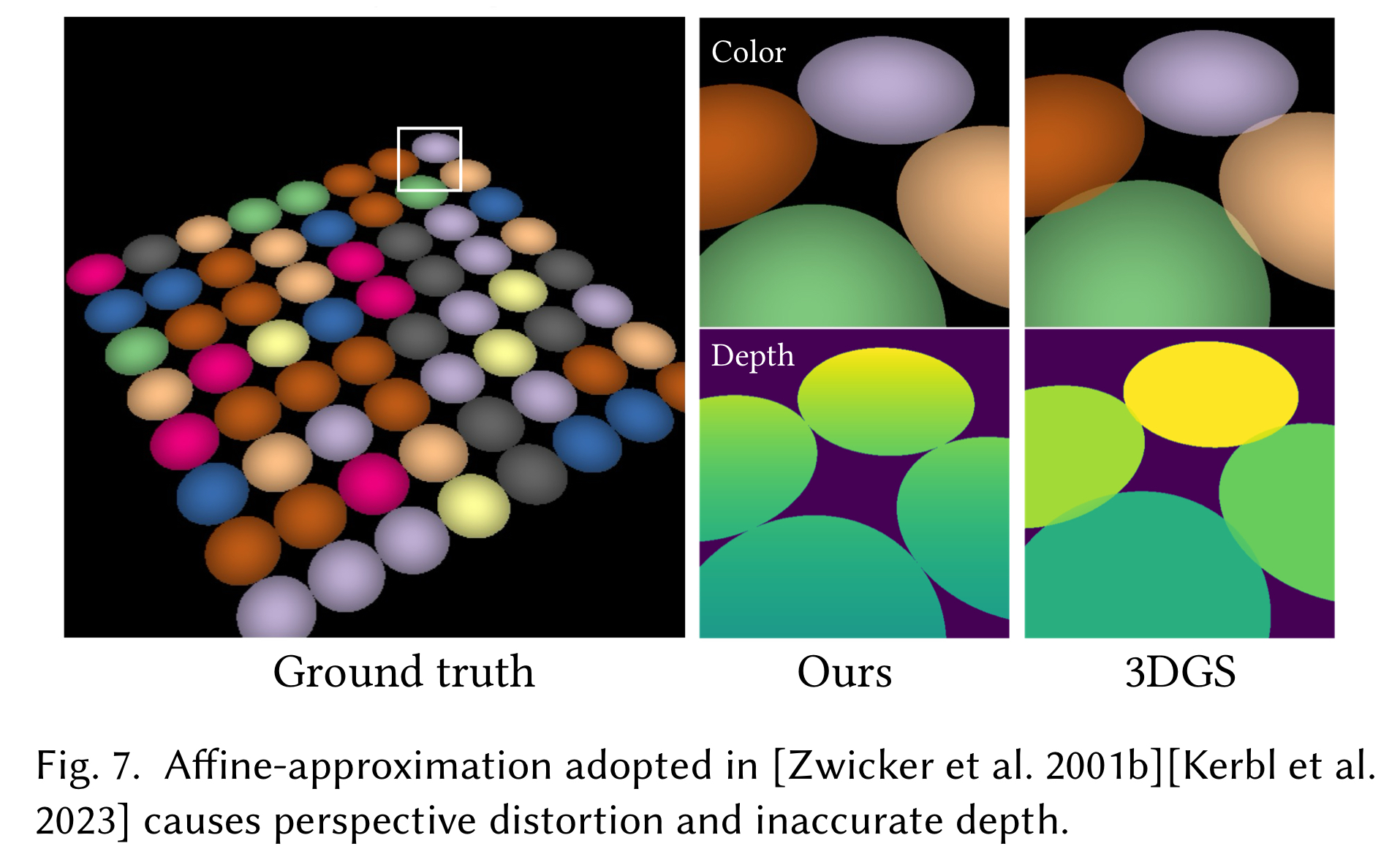
- Affine Projection 이 정확하지 않다
3D GS 를 radiance fiels 로 변환하는 데 사용되는 affine matrix 는 () Gaussian center 에서 벗어나면 원근 정확도가 떨어진다. 이로 인해 종종 noise 가 많은 reconstruction 결과가 나타난다.
- c.f. 짧게 첨언하자면, Jacobian 를 사용하는 affine projection 은 1st Taylor Approximation 이기 때문에 center point 에서 벗어날수록 projection error 가 커지게 된다.
또한 논문에는 언급되지 않았지만, 3D GS 는 Mesh Reconstruction 에도 어려움을 겪는다. NeRF와 마찬가지로 opacity 의 accumulation 으로 volume 을 표현하기 때문에 Marching Cube / Poisson Reconstruction 등의 방법으로 좋은 퀄리티의 mesh 를 생성하기 요원한 것.
1.3. SuGaR: Surface-Aligned Gaussian Splatting
상기 Surface Reconstruction 의 어려움을 해결하기 위해 2) surface normal 관점으로 문제를 해결하려 한 previous work 이 있는데, 그 연구가 바로 concurrent work 로 소개하는 SuGaR 이다.
SuGaR 의 핵심 idea 는 바로
- 잘 훈련된 3D Gaussians 은, 가장 짧은 scale 을 갖는 axis 가 surface normal 과 평행할 것이다
라는 가정이다.
즉 앞서 정의한 3D Gaussians 를 다음과 같은 approximation 으로 대체할 수 있게 되고,
이러한 constraint 를 regularization 으로 활용하여 3D GS 를 surface aligned 하게 만든다.
하지만 SuGaR 는 3D GS 를 먼저 학습한 후 refinement 를 거치는 2-stage 이기 때문에 학습 방식이 복잡하며, surface reconstruction 어려움의 원인이었던 projection 의 부정확함에 대해서는 해결하지 못하기 때문에 SuGaR 를 custom scene 에 적용해보면 원하는 바 만큼의 깔끔한 geometry 로 mesh 를 생성하지 못하는 경우가 많았다.
2. 2D Gaussian Splatting
2.1. 2D Gaussian Modeling (Gaussian Surfels)
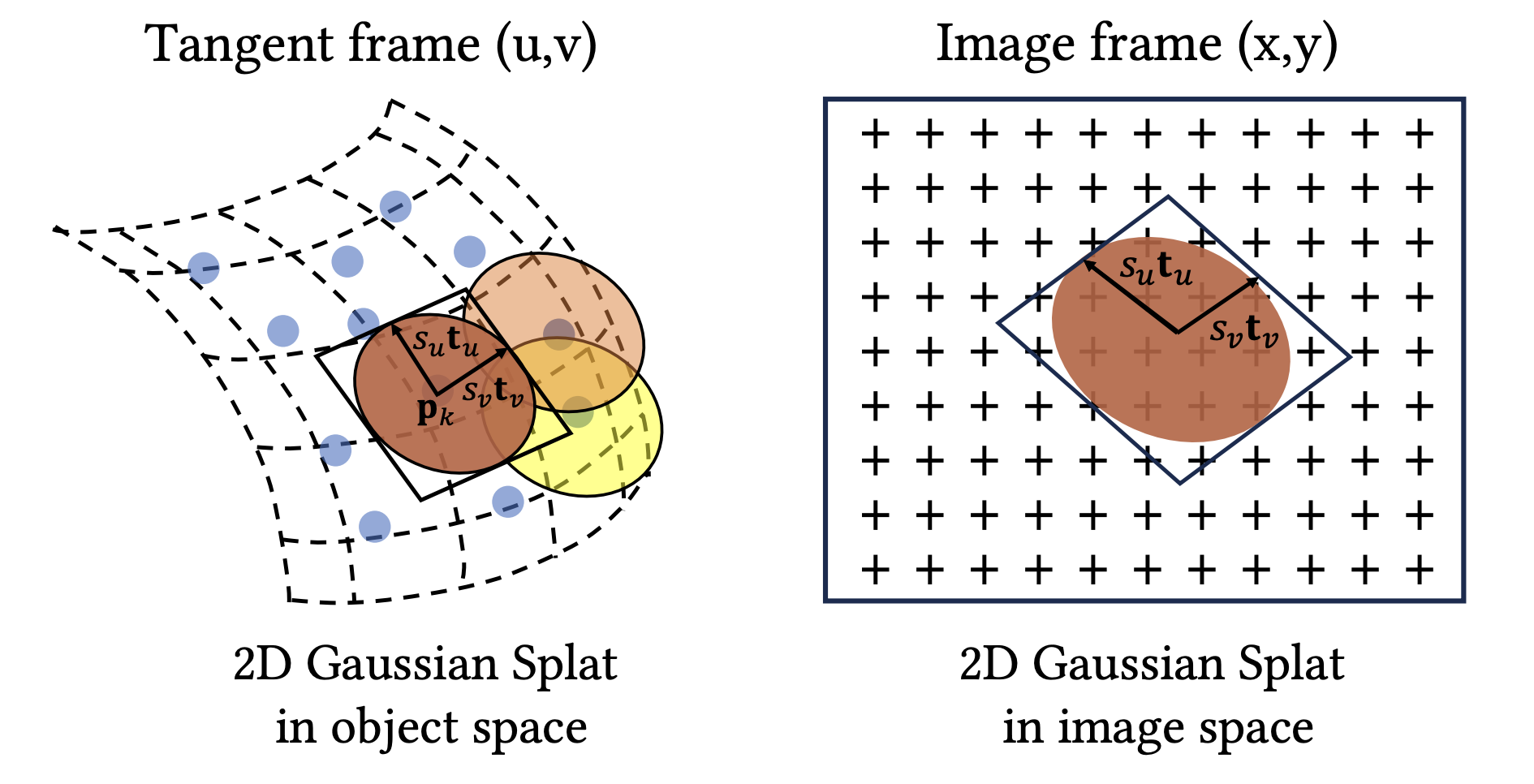
2D Gaussian Splatting 의 접근법은 크게 보면 SuGaR 의 intuition 을 반대로 뒤집은 것에 불과하다. 즉 3D Gaussian 을 flat 하게 만들어서 surface 에 정렬시키지 말고 (SuGaR), 처음부터 flat 한 2D Gaussian (surfels) 로 이루어진 scene 을 학습시키자는 것이다.
따라서 우리가 배워야 할 Rotation Matrix 과 Scale Matrix 은 다음과 같이 정의할 수 있다.
이제 2D Gaussian 을 world space 에서 center point , tanget vector 를 갖는 local tangent plane 에서 정의할 수 있으며, 이때 plane 는 다음과 같을 것이다.
따라서 frame 에서 2D Gaussian 을 다음과 같은 standard 2D Gaussian fucntion 으로 표현된다.
결론적으로 2D GS 에서 학습할 parameter 는 rotation axis 와 scaling , opcaity 와 Non-Lambertian color 에 대한 Spherical Harmonics coefficient 가 된다.
2.2. Splatting
2.2.1. Accurate 2D-to-2D Projection in Homogeneous Coordinates
2D Gaussian 은 원론적으로는 zero scale 만 추가하여 3D GS projection 을 그대로 사용할 수 있다. 하지만 앞서 언급한것처럼, 3D GS 의 affine projection 은 1st Taylor Expansion 만을 사용하기 때문에 center point 에서 멀어질수록 approximation error 가 커지게 된다.
- figure: 관련 내용을 언급한 official repo FAQ

2D GS 의 저자들은 부정확한 3D GS 의 original projection 을 사용하는 대신, 2D Gaussians projection 으로 hoogeneous coordinates 를 이용한 일반적인 2D-to-2D mapping 을 사용할 것을 제안한다.
World-to-screen transformation matrix 에 대하여, sceen space (2D) 상의 point 는 다음과 같은 관계를 갖는다.
이는 camera space 에서의 point 에서의 c2w direction ray 가 2D splats 과 depth 에서 교차한다는 의미이며, sceen space 의 point 의 Gaussian density 를 다음과 같이 얻을 수 있을 것이다.
하지만 inverse transform 은 numerical instability issue 가 있으며, threhold 사용 등으로 이를 우회하려해도 unstable 한 optimization 을 초래할 수 있다.
2.2.2. Ray-Splat Intersection
따라서 저자들은 ray-splat 의 교점을 3개의 non-parallel plane ( plane, -homogeneous plane, -homogeneous plane) 의 교점을 구하는 방법으로 이를 해결한다.
Given image coordinate 에 대하여, 우리는 ray 를 두 homogeneous -plane 와 -plane 사이의 교선으로 정의할 수 있으며, world space 에서 정의된 homogeneous plane 와 를 -space 상으로 tranform 하여 교점을 구할 것이다.
, homogeneous plane 을 space 상의로 transform 하여 구한 두 plane , 은 다음과 같으며,
screen space 를 지나는 c2w direction ray 와 2D Gaussian Splats 의 교점은 다음과 같이 linear equation 의 closed-form solution 으로 구할 수 있다.
상기 공식을 통해 screen pixel 에 대한 -space 에의 projection value 를 알 수 있으며, 앞서 정의한 수식 을 통해 depth 도 얻을 수 있다.
논문 supplementary material 에 2D GS 의 2D-to-2D projection 과 3D GS 의 affine projection 을 비교한 figure 를 보면, 확실히 homogeneous projection 이 더 정확한 모습을 보여주고 있다.
2.3. Training 2D GS
2D GS 의 학습에 사용되는 loss 는 앞서 정의된 2D projection / rasterization 을 이용한 image rendering loss 외에, 추가적인 2가지 regularization loss 가 사용된다.
2.3.1. Depth Distortion
NeRF 와는 다르게, 3D GS 의 volume rendering 은 교차하는 splats 간의 거리 차이를 고려하지 않는다. (NeRF 는 로 sampling point 간 거리를 고려한 rendering 을 계산한다. cf. discretizatized volume rendering in NeRF)
따라서, 널리 퍼진 gaussian splats 들은 비슷한 color 와 depth 를 가질 수 있으며, 이는 ray 가 first visible surface 만 정확히 한 번 교차해야 하는 surface reconstruction 을 어렵게한다.
이 문제를 완화하기 위해, 저자들은 Mip-NeRF360 와 비슷하게 ray weight distribution 을 ray-splat 교점 근처로 집중시키는 depth-distortion loss 를 제시하였다.
여기서 각 변수는 th ray-splat 교점에 대해 다음과 같은 의미를 갖는다.
- : blending weight
- : depth
weight 에 대한 정의를 보면 NeRF 의 accumulated transmittance 와 같은 식임을 알 수 있는데, 같은 논리로
- point 가 현재 ray direction 을 따라 투명하면서
- point 의 opacity 값이 높을 때
큰 값을 나타내는 weight 가 된다. 즉 해당 loss 는, opacity 가 높은 ray-splats 교점들의 깊이 차이를 줄이도록 하는 regularization 이 된다.
또한 이 Loss 구현에 대해서 appendix 에 자세하게 언급되어 있는데,
where , , and .
각 모두 opacity 의 accumulation 혹은 opacity x depth 의 accumulation 등으로 이루어진 항임을 알 수 있다.
따라서, 위의 공식처럼 이 loss 를 일종의 image rendering 처럼 계산할 수 있다. 실제 2D GS 구현체에서도 rasterizer 단에서 이를 처리하여 backpropagation 한다.
2.3.2. Normal Consistency
Depth-Distortion Loss 에 더불어, 모든 2D splats 이 실제 surface 와 정렬되도록 하는 normal-consistency loss 를 제시한다.
Volume Rendering 은 반투명한 여러 2D Gaussians (surfels) 가 ray 를 따라 존재할 수 있기 때문에, 저자들은 accumulated opacity 가 0.5 에 도달하는 부분을 실제 surface 라고 간주하였다.
그리고 이 부분에서의 surfel's normal 과 depth 의 derivative 를 align 하는 normal consistency loss 를 다음과 같이 제안한다.
여기서,
- 는 ray 을 따라 교차하는 splats 의 index
- 는 ray-splat 교점의 blending weight
- 는 splat 의 normal vector
- 은 인근 depth map 의 point 에서 추정된 normal vector 이다
구체적으로, 은 finite difference 을 사용하여 다음과 같이 계산된다.
실제로 visualize 해서 보면 두 normal 의 차이가 보여서 흥미로운데, surface normal 의 경우는 훨씬 smooth 한 모습을, depth 에서 계산한 normal 은 조금 더 detail 하게 geometry 를 반영하는 모습을 보여준다.
- Figure: Normal vs Depth2Normal, captured in my custom viewer

3. Experimens & Custom Viser Viewer
3.1. Qualitative Results & Custom Object Reconstruction
PSNR 자체는 이전 연구에 비해 뛰어나지 않기 때문에 와닿지 않을 수도 있지만, 이 연구의 진가는 정성평가와 실제 이 알고리즘을 테스트 해봤을 때 드러난다.

논문에서 드러나는 타 논문 대비 2D GS 의 surface recon / mesh recon 성능은 이전 연구 그 무엇과도 비교를 불허한다.
또한 이러한 성능이 실제 custom scene 에도 그대로 적용된다. 아래는 개인적으로 가지고 있는 두 가지 object 를 실제로 촬영하고 2D GS 를 통해 mesh export 해본 실험 결과이다.
-
2D GS: guitar (mesh)
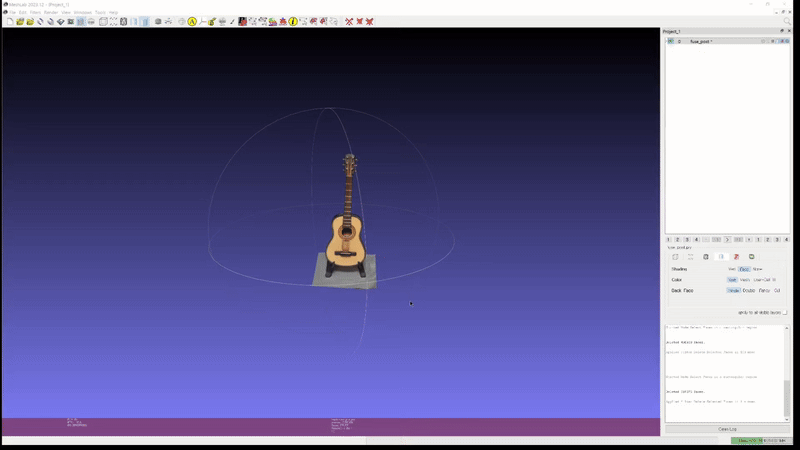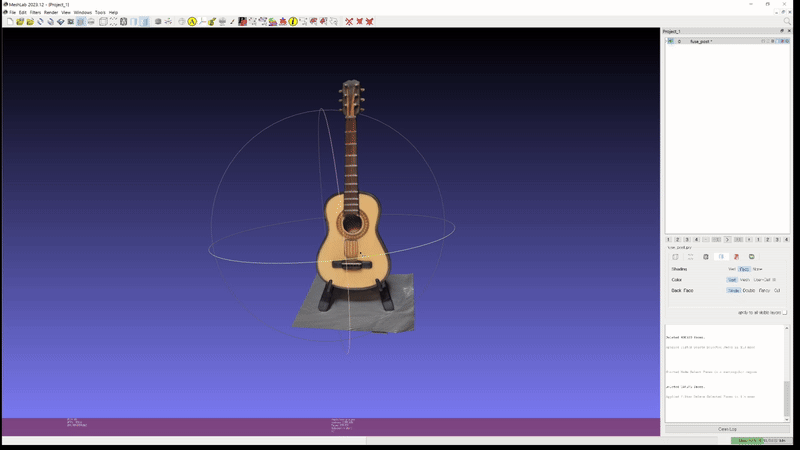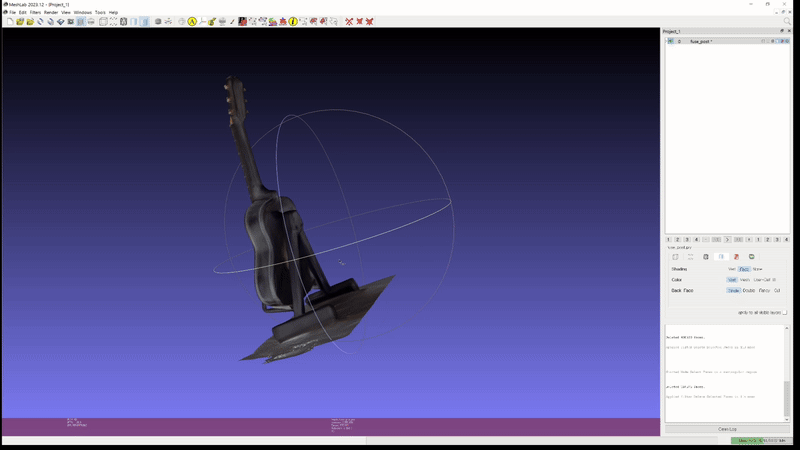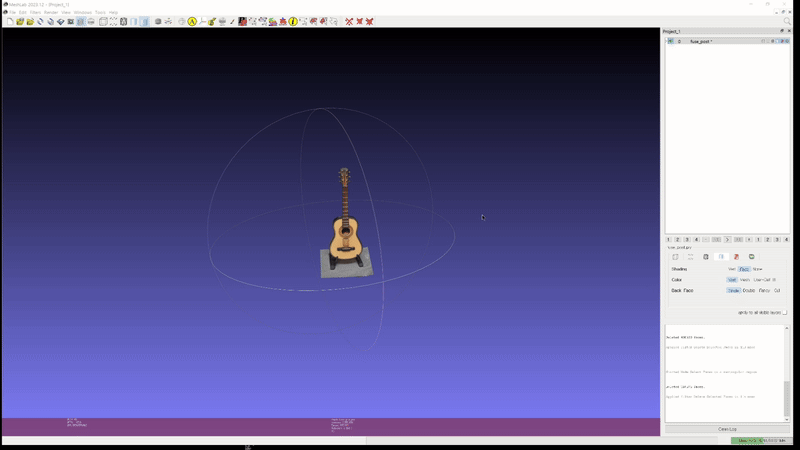
-
2D GS: penguin (mesh)
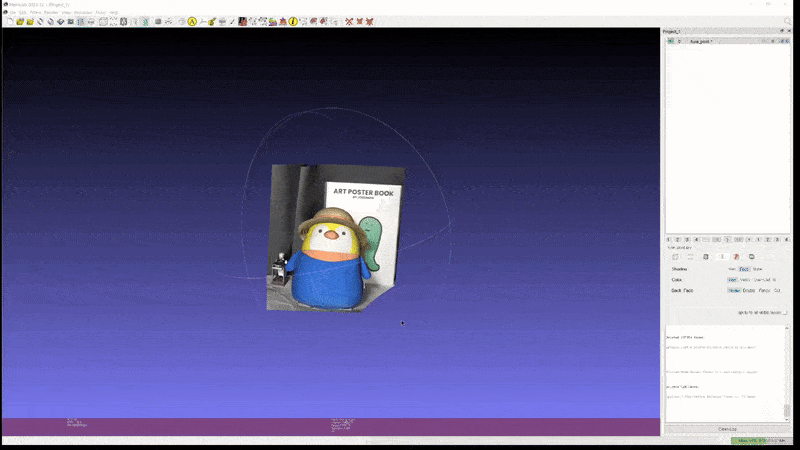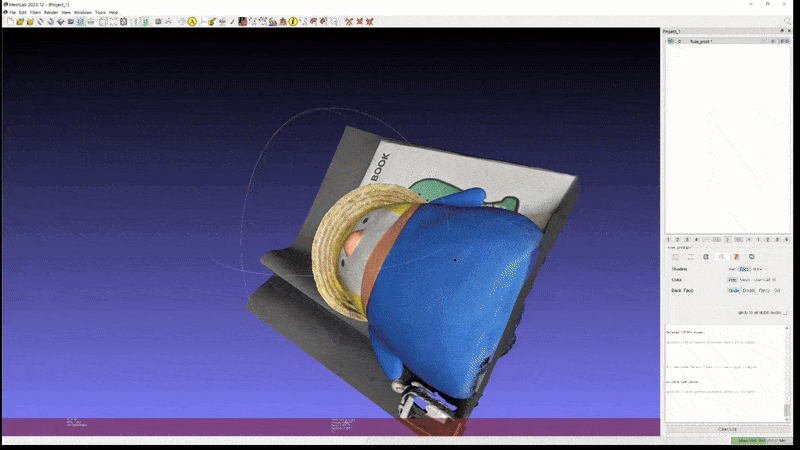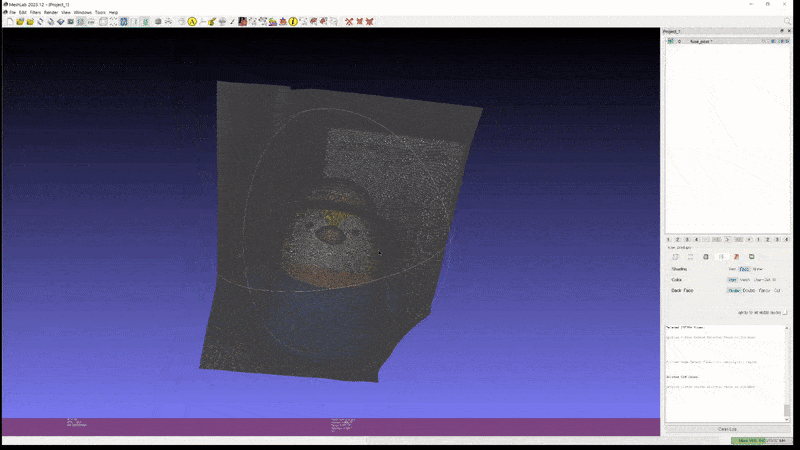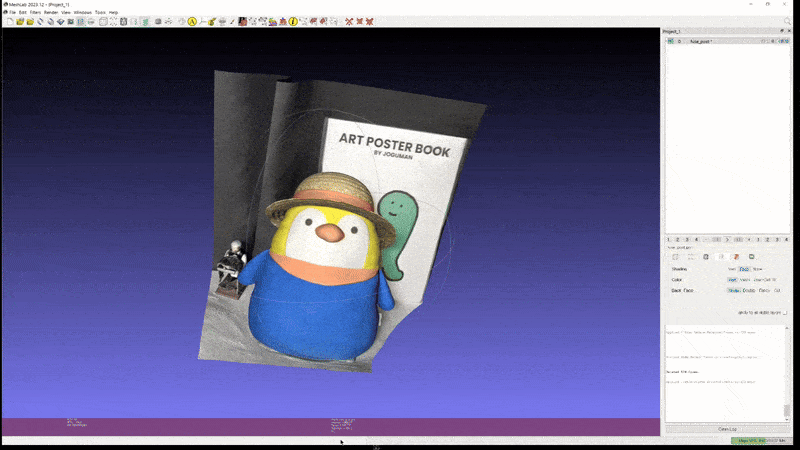
이 정도의 성능이라면 light-condition disentanglement 문제만 어느 정도 해결된다는 가정 하에 실제 게임/모델링 등의 작업에도 사용할 수 있을만한 퀄리티라고 생각된다.
또한 2D GS 는 depth 값을 (비교적) 정확하게 뽑을 수 있기 때문에, estimated depth 을 사용하여 TSDF reconstruction 으로 mesh 를 빠르게 생성할 수 있다. (실험했을 때는 1분 이내였다)
cf. 해당 논문이 발표된 SIGGRAPH'24 에 정확하게 같은 idea 로 발표된 연구 Gaussian Surfels 도 있지만, 3rd axis 를 1st, 2nd axis 의 cross-product 로 사용하기보단 따로 3rd axis 를 배우되, scale 만 0으로 표현하여 original 3D GS 의 rasterization 을 그대로 사용한다. 즉 affine projection error 를 해결하지 못한다. 실제 알고리즘을 테스트 해봤을 때도 2D GS 가 Gaussian Surfels 에 비해 월등한 성능을 보여주었다.
3.2. Custom Viser Viewer for 2D Gaussian Splatting
2D GS 연구에 한 가지 아쉬운 점은, 현재로서는 official viewer 를 제공하지 않는다는 점이다.
(24.06.10 부터는 SIBR Viewer 를 제공하는 중이다)
2D GS 의 mesh export 가 TSDF 를 사용하기 때문에 mesh 가 꽤나 빠르게 뽑히지만, truncation distance 에 따라 clustering 이 잘못되어 나오는 mesh 가 생기는 등, 일부 hyperparamter tunning 이 필요하다.
그런데 mesh 에 surface artifacts 가 존재하는 경우, 실제 scene 학습이 잘못된 것인지 truncation distance 를 튜닝해야 하는 문제인지 판별하기 어렵다.
2D GS ply 파일에 additional scale dimension 을 추가하여 해당 값을 0으로 할당하면 3D GS viewer 를 그대로 사용할 수 있지만, 2D GS 저자들의 main contribution 중 하나인 정확한 gaussian projection 을 사용할 수 없다.
따라서 viser 를 이용해서, 2D GS 의 homogeneous projection 을 사용하여 2D GS ply 파일을 볼 수 있는 custom viewer 를 만들어 보았다.
⭐ Github Project Link

-
Viser 를 이용해서 구현하였으며, 2D GS 의 homogeneous projection 을 그대로 사용하여 projection error 가 없다.
-
Normal / Depth / Depth2Normal / Pointcloud 등 다양한 visualization 을 지원한다.
-
Splats 에 대한 delete, transform 등 다양한 편집 기능을 지원한다
-
train 시에도 viewer 로 scene 이 train 되고 있는 모습을 볼 수 있다
-
Rendering camera path 를 생성하고 preview 를 제공한다
-
Official repo 에서 언급되었다~ :)

쉽게 생각하고 구현을 시작했었는데 은근히 작업하면서 신경 쓸 게 많았다. 조만간 viewer 개발기도 올려볼 생각이다.
- cf. Viewer 개발기
4. Conclusion
당장 몇개월 전만 해도 아직 NeRF / 3D GS 의 실사용은 힘든 단계라고 글을 썼던 것이 무색하게 좋은 알고리즘이 공개되었다.
단순히 3D GS 를 flat 하게 핀 것에 불과한 Gaussian Surfels 연구에 비해서도, projection 의 부정확함, rasterization 등을 섬세하게 고려해서 잘 설계한 알고리즘이라는 생각이 든다.
2D GS 는 3D GS 가 가지는 explicit representation 의 장점을 그대로 계승하면서도, 3D GS 가 갖는 surface reconstruction 의 어려움, projection error 등을 해결한 진일보한 연구이다.
또한 요새 연구들이 project page 만들기에 공을 들이는 것에 비해 실제 test 결과는 project page 결과를 따라가지 못할 때도 많은데, 실제 custom scene 에도 공개된 것 정도의 성능을 보여주는 것도 만족스러웠다.
You may also likes:

와 감사합니다!