SDF (Signed Distance Function) 와 Eikonal Equation 의 관계는?

Hwan Heo·2024년 5월 28일

Implicit Neural Network NeRF NeuS Radiance Fields Signed Distance Function Surface Reconstruction eikonal eikonal equation eikonal loss sdf

Neural Rendering

목록 보기

11/17

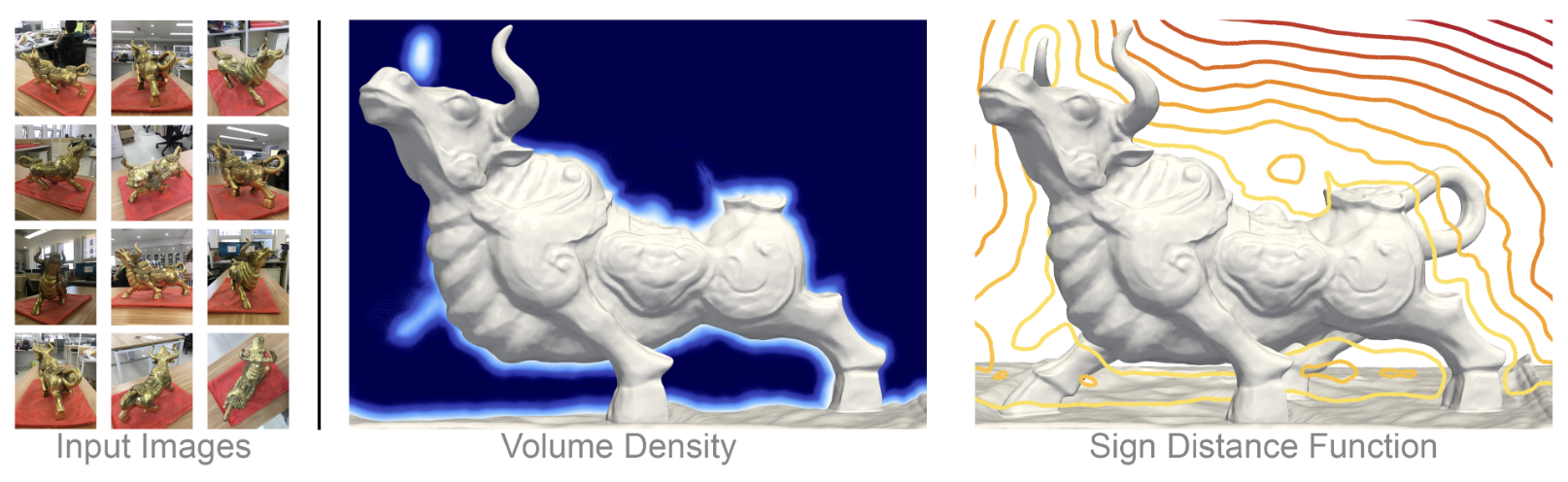
Neus 등의 SDF 학습을 위해 사용하는 eikonal loss 를 유도해보자!

1. 들어가며: SDF & Surface Reconstruction

블로그에서는 잘 다루지 않았지만, Implicit Neural Network 가 주요 task 로 다루는 것은 NeRF 를 위시한 Novel View Synthesis 뿐만이 아니다. NeRF 만으로 풀기 어려운 문제들도 상당히 많으며, 그 중 대표적인 문제가 바로 Surface Reconstruction 이다.

Radiance Fields 계열의 기술들은 3D scene reconstruction 을 위해 주로 opacity 값을 누적하여 간접적으로 표면을 처리하는 방식을 사용한다. 이러한 접근 방식은 장면 전체를 표현하는 데는 효과적이지만, 정확한 surface reconstruction 에는 취약하다.

이와 대조적으로 SDF (Signed Distance Function)는 3D surface reconstruction 에 훨씬 특화된 모델이다. SDF는 공간 내의 각 점에 대해 해당 점에서 표면까지의 최단 거리를 나타내며, 그 거리 값이 0인 점들의 집합, 즉 zero-level set (isosurface) 이 바로 실제 surface 를 정의하게 된다.

NeRF 와 마찬가지로, MLP 로 이러한 SDF function 을 근사하게 되며, 다음과 같은 주요 연구들이 있다.

figure credit: Neuralangelo

이러한 SDF 계열 논문을 읽다 보면, 필연적으로 마주하게 되는 공식이 바로 eikonal equation,

\| \nabla f_\text{SDF} \| = 1 \\

와 이를 통해서 유도된 eikonal regularization term (or eikonal loss)

\arg \min_\theta \mathbb E_x \left ( \| \nabla f_{\text{SDF}}(x) \| -1 \right )^2

이다. ( $\theta$ : MLP's parameter)

이 글에서는 SDF 학습이 왜 이러한 eikonal equation 을 푸는 것과 동치인지 알아볼 것이다.

2. SDF to Eikonal Equation

공간을 점유하고 있는 어떠한 object $\Omega \in \mathbb{R}^3$ 와 이 object 의 boundary $\partial \Omega$ 에 대하여, 우리는 SDF (Signed Distance Function) $f_{\Omega}(x)$ 을 다음과 같이 정의할 수 있다.

f(x) = \begin{cases} d(x, \partial \Omega) & \text{if } x \in \Omega \\ -d(x, \partial \Omega) & \text{if } x \in \Omega^c \end{cases}

여기서 $d(x, \partial \Omega)$ 는 $x$ 와 boundary $\partial \Omega$ 사이의 distance 이다.

d(x, \partial \Omega) = \inf_{y \in \partial \Omega} \|x - y\|

이제

삼각부등식과 경로 적분을 이용하는 방식
기하학적인 직관을 이용한 조금 더 간단한 방식

두 방법으로 SDF function 이 eikonal equation 을 만족함을 증명하겠다.

2.2. Proof 1: Using the Triangle Inequality and Path Integration

2.1.1. Upper bound of the SDF's gradient

$\Omega$ 내의 임의의 두 점 $x$ , $y$ 와 이를 잇는 선분 $\{x + t(y - x) : t \in [0, 1]\} \subseteq \Omega$ 에 대하여, 삼각부등식으로 다음이 성립한다.

f(y) \leq \|y - x\| + f(x)

이제 이 식으로부터, $y=x+at, \ (a \in \mathbb{R}^n)$ 로 치환하여 대입해보면 다음과 같은 부등식을 얻는다.

\frac{f(x + at) - f(x)}{t} \leq \|a\|

여기서 $t \to 0$ 으로 보내 극한값을 구해보면

a \cdot \nabla f \leq \|a\|

임을 알 수 있고, 따라서 $\| \nabla f(x) \| \le 1$ 이 성립한다.

2.1.2. Lower bound of the SDF's gradient

$x \in \Omega$ 에 대하여, $\{y(t) : t \in [0, 1],\ y(0) = x, y(1) \in \partial \Omega\}$ 가 $x$ 와 boundary $\partial \Omega$ 사이의 shortest path 라고 가정하자.

이 경우, 모든 $t \in [0, 1]$ 에 대하여 SDF $f$ 는 다음과 같이 표현할 수 있다.

f(y(t)) = \int_1^t \|\dot{y}(t)\| \, dt

이는 $y(t)$ 가 $x$ 와 boundary $\partial \Omega$ 사이의 최단 경로에 있기 때문에, $y(t)$ 와 boundary $\partial \Omega$ 사이의 거리가 해당 경로의 길이와 같음을 의미한다.

따라서 위의 방정식을 미분하면 다음을 얻을 수 있고,

\dot{y}(t) \cdot \nabla f(y(t)) = -\| \dot{y}(t)\|

Cauchy–Schwarz inequality 에 의해

\| \dot{y}\| \| \nabla f\|\ge |\dot{y} \cdot \nabla f|=|−\|\dot{y}\|| \\

을 만족하므로

\|\nabla f(y(t))\| \geq 1

임을 알 수 있다.

2.2. Proof 2: Using Geometric Intuition

2.2.1. Gradient of the Distance Function

Distance Function $d(x, \partial \Omega)$ 는 boundary $\partial \Omega$ 수직인 방향으로 최단 거리를 측정한다. 정의에 따라 distance function 의 gradient 는 distance 값이 steepest ascent 하는 방향, 즉 surface normal direction 과 같아야 할 것이다.

따라서 distance function 의 gradient 는 다음과 같다.

\nabla d(x, \partial \Omega) = \frac{x - y}{\|x - y\|} \\ \text{where } y =\arg \min_{y \in \partial \Omega} \|x-y\|

2.2.2. Norm of the gradient

$x \in \Omega$ :
$f(x) = d(x, \partial \Omega) \Rightarrow \|\nabla f(x)\| = \|\nabla d(x, \partial \Omega)\| = 1$
$x \in \Omega^c$ :
$f(x) = -d(x, \partial \Omega) \Rightarrow \|\nabla f(x)\| = \|-\nabla d(x, \partial \Omega)\| = 1$

distance function 의 gradient 는 unit vector 이므로 그 norm 은 항상 1 이다.

따라서, 모든 $x \in \mathbb{R}^n$ 에 대하여 eikonal equation

\|\nabla f(x)\| = 1

이 만족한다.

3. Conclusion?

그래서 어쩌라고? 저 식이 무슨 의미인지 알면 SDF 학습이 더 잘되나?

그런 것은 아니다. 오히려 저 식은 SDF 학습이 어렵게 하는 주범 중의 하나이다.

eikonal loss term 을 계산하려면 MLP 에 대한 second derivative 가 필요한데, INN 전가의 보도로 등장하는 Instant-NGP, tcnn library 에는 공식적으로 second derivative 기능을 제공하지 않는다.

그래서 Hash-Grid (feature-grid) representation 을 사용하는 SDF method 는 gradient 를 analytic 하게 계산하는 대신 finite difference 를 이용하여 numerical gradient 를 계산한다.

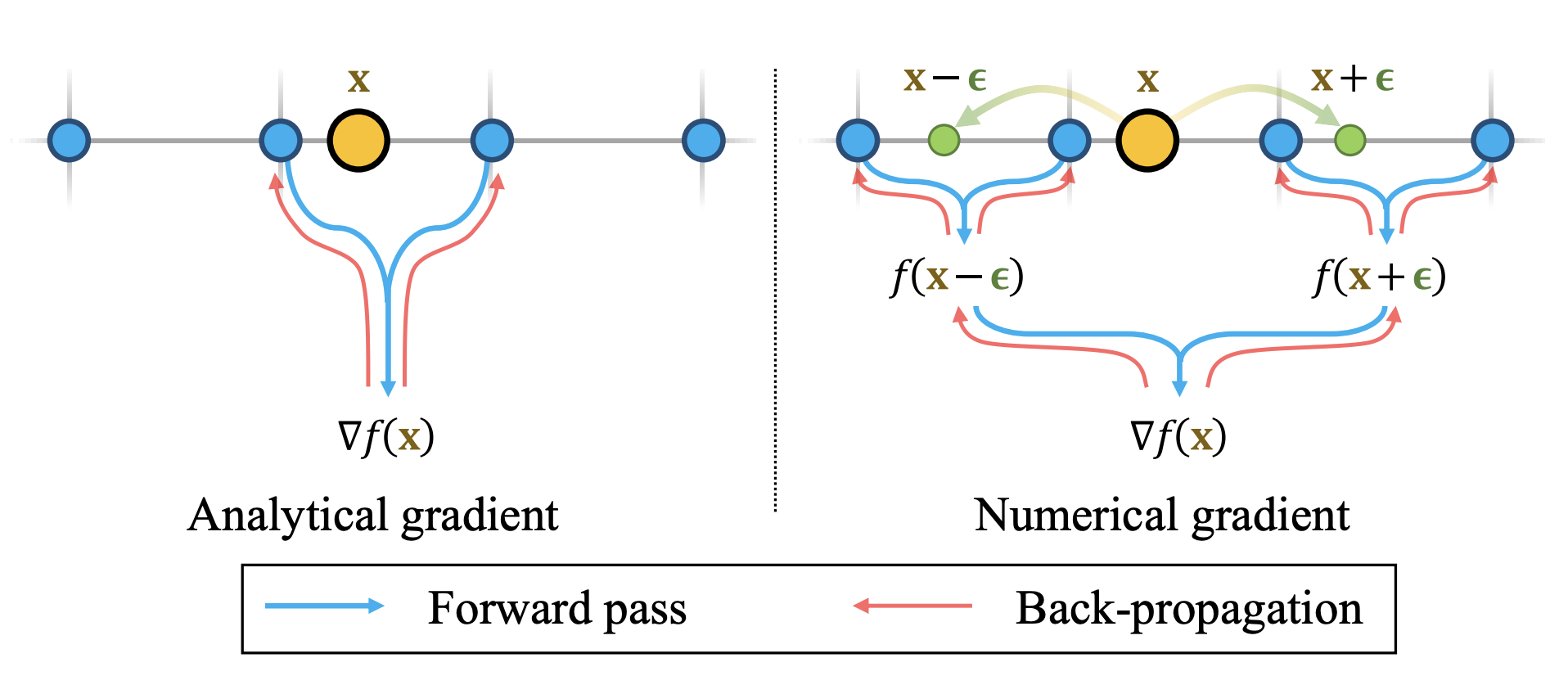
대표적으로, 인용했던 Neuralangelo 등이 해당 방식을 통해 gradient 를 계산하며, 이는 neuralangelo 의 original Instant-NGP 대비 학습 시간 증가의 원인 중 하나이다.

SDF는 second derivative 까지는 근사할 필요가 없는 NeRF 보다 복잡하지만, 더 정확한 3D surface 를 얻을 수 있다는 점에서 그 가치가 있다. 이러한 SDF 의 핵심적인 문제가 eikonal equation 을 잘 근사하는 것이므로, 수학적으로 정확히 이해하는 것이 SDF 학습의 최적화된 방법을 찾아가는 첫 단계라고 믿는다.

cf. https://math.stackexchange.com/questions/3605929/signed-distance-function-and-the-eikonal-equation