[Review] PlenOctrees for Real-time Rendering of Neural Radiance Fields

Hwan Heo·2022년 7월 7일

Implicit Neural Networks NeRF Neural Rendering

NeRF

목록 보기

3/8

NeRF 등의 neural rendering 기법은 강력한 3D novel view synthesis 성능을 자랑하지만, non-lambertian effect (view-dependent color change) 를 모사하기 위해서 rendering view 가 바뀔 때마다 MLP query 를 다시 행해야 하는 단점이 있다. 이 논문은 Spherical Harmonics 를 통해 color 를 factorization 함으로써 density 와 color 를 voxelize 하여 저장할 수 있게 하여 기존 NeRF 보다 3000배 이상 빠른 real-time rendering NeRF 기법을 제시한 연구이다.
ICCV2021 Oral

1. Introduction

NeRF 등의 Neural Radiance Fields 를 이용하는 Neural Rendering 은 scene 에 대한 projected color 를 ray casting 방식으로써 계산한다. Discreatized 된 color 는 다음과 같이 쓸 수 있는데,

C(r) = \sum_{i=1}^{N} T_i \cdot (1- \text{exp}(-\sigma_i \delta_i)) \cdot c_i, \ \quad \text{where }T_i = \text{exp} \bigg( - \sum_{j=1}^{i-1}\sigma_j \delta_j \bigg )

한 픽셀의 color estimation 을 위해서는, $N$ 번의 MLP query 가 필요함을 알 수 있다.

만약 우리가 800x800 resolution 으로 scene 을 렌더링 하기 위해서는, 800x800x192 (64 coarse and 192 fine) 이 필요하며, 이는 neural radiance fields 가 8 layer 의 shallow 한 MLP 임에도 불구하고 NeRF 의 real time rendering 을 어렵게 만드는 주요한 원인이다.

이러한 단점을 해결하기 위해, Memory-Inference Tradeoff 로써 미리 density 등의 값을 계산한 후 voxelize 하여 저장하는 방법 등을 생각해볼 수 있으나, NeRF 는 view-dependent 하게 color 가 바뀌기 때문에 이를 미리 모두 계산하고 저장하는 것은 불가능하다.

이 논문은 voxel 위의 한 점의 color 를 Spherical Harmonics 로 factorize 하는 방법을 통해 SH 의 coefficient 만을 저장하여 octree 구조로 voxelized NeRF 를 caching 하는 방법을 제안한다. 이를 통해 150fps 수준의 rendering 속도를 달성하였다.

2. Method

2.1. NeRF-SH: NeRF with Spherical Harmonics

2.1.1. Color Factorization with Spherical Harmonics

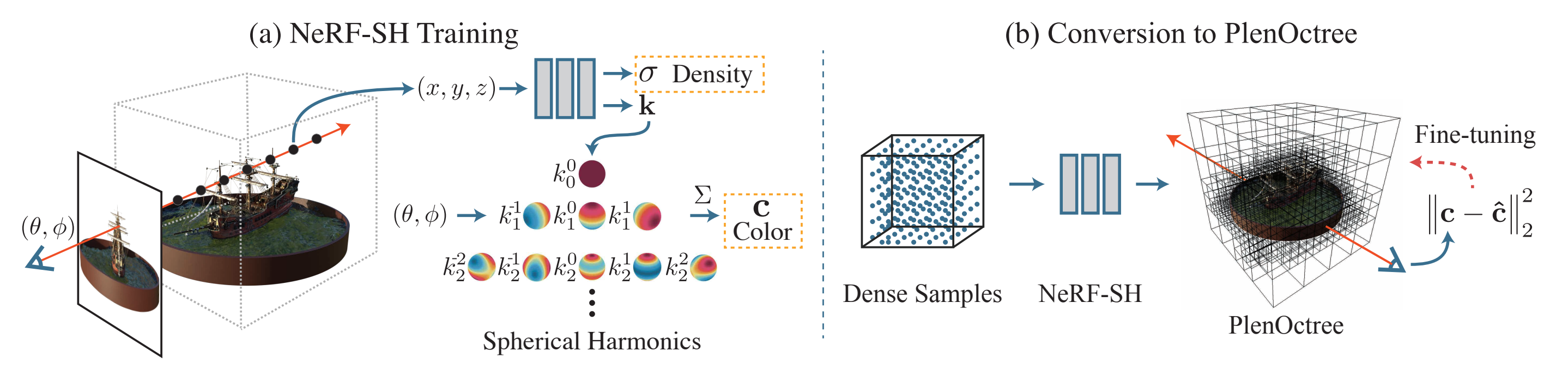
앞서 말했듯, NeRF 의 voxelize 의 가장 큰 장애물은 non-lambertian effect 를 표방하는 NeRF 의 color estimation 이다. view-dependent 하게 변하는 color 를 표현하기 위해 original NeRF 는 rendering viewpoint 가 바뀔 때마다 새로운 MLP inference 가 필요하고, voxel 의 한 점에서 가능한 모든 각도에 대한 color 를 저장하는 것은 불가능하기 때문에 NeRF 를 naive 하게 caching 하는 것은 challinging problem 이다.

따라서 저자들은 NeRF 의 output 을 RGB 값이 아닌 Spherical Harmonics 의 각 coefficient 를 예측하도록 수정하였다.

f(\mathbf x) = (\mathbf k, \sigma) \quad \text{where } \mathbf k = (k_l^m)^{m:\ -l \le m \le l}_{l: \ 0\le l \le l_\text{max}}

여기서 $k_l^m\in \mathbb R^3$ 으로, 각 RGB 를 독립적으로 나누어서 SH factorization 으로 근사한다.

Spherical Harmonics 란 Sphere 상에서 Laplacian Equation ( $\Delta f = 0)$ 을 으로 만드는 function basis 들로, 각 SH 들이 독립적으로 특정 각도에 대한 scalar value 를 embedding 하고 있다. 위 그림 (a) 의 SH visualization 에서 이를 확인할 수 있는데, SH basis 를 통한 factorization 으로 non-lambertian color 를 표현할 수 있음을 알 수 있다.

이제 우리는 각 SH coefficient 값들을 통해 view-dependent color $\mathbf c(\mathbf d; \mathbf k)$ 를 다음과 같이 구할 수 있다.

c(\mathbf d, \mathbf k) = S \bigg ( \sum_{l=0}^{l_\text{max}} \sum_{m=-l}^{l} k_l^m Y^m_l (\mathbf d) \bigg ) \\ \text{where } S:x \rightarrow (1+\exp(-x))^{-1}, Y^m_l :\text{spherical harmonic function}

이를 NeurIPS2020 Neural Sparse Voxel Fields (NSVF) 관점에서도 생각해볼 수 있는데, plenoctrees 와 비슷하게 NSVF 도 NeRF 를 voxelize 하여 저장하려고 하지만, 앞서 언급한 non-lambertian color estimation 을 위해 SH coefficient 가 아닌 32 dimension 의 feature vector 들을 각 voxel point 에 저장한다.

즉 NSVF 는 implicit 한 feature vector 로 이루어진 voxel grid 와 이에 대한 lightweight MLP 를 통해 fast rendering 을 구현했다면, plenoctrees 는 이와 반대로 explicit 한 feature (i.e. coefficients of SH) 로 이루어진 voxel grid 와, explicit 한 spherical harmonic functions 을 통해 faster rendering 을 구현한 것.

NSVF 와는 반대로 SH functions 들은 closed form 으로 알려져 있으므로

Y^m_l: \mathbb S^2 \rightarrow \mathbb C \\ Y^m_l(\theta, \phi)= \sqrt{ {2l+1 \over 4 \pi } { (l-m)! \over (l+m)!} } \ P^m_l (\cos \theta ) e^{im\phi}

NSVF 보다 (~1fps) 훨씬 빠른 rendering (~150fps) 이 가능하다.

2.1.2. Sparsity Prior Loss

Image quality 와는 별개로, 효율적인 voxel grid 의 구현을 위해서 저자들은 sparse 한 region 에 대한 surpass 역할을 하는 loss 를 추가하였다.

\mathcal L_{\text{sparsity}} = {1 \over K} \sum_k |1 - \exp(-\lambda \sigma _k) |

어떠한 particle 의 density $(\sigma)$ 가 클 때에만 projected color 에 기여하므로, 위 loss 는 solid 하지 않은 particle 들의 density 값을 0으로 만들어준다.

2.2. PlenOctree: Octree-based Radiance Fields

2.2.1. Rendering

Voxelized 된 NeRF-SH 의 rendering 과정은 매우 간단하다.

Ray-Voxel intersections 을 구하고 (closed form)
Original NeRF 와 같이 discreatized ray casting 을 계산

실제 test 과정에서는, accumulated transmittance $T_i$ 값이 일정 threshold (0.01) 이하면 (즉, 굉장히 높은 확률로 빈 공간을 나타내는 ray) early stopping 하여 속도를 더욱 높였다고 한다.

2.2.2. Conversion from NeRF-SH

다음 세 과정을 거쳐서 voxelize 한다. 요약하면 solid 한 particle 이 있는 voxel grid 만 남겨서 그 안에서 sampling 을 통해 factorized 된 color 를 저장하는 과정이다.

Evaluation: density value $(\sigma)$ 를 저장하는 uniformly spaced 3D voxel grid 를 구성한다.
Filtering: threshold $\tau_w$ 보다 작은 density 값을 갖는 voxel 은 제거한다. 즉 sparse voxel grid 를 구성
Samplinge: filtered voxel 에 각 256 개의 random points 를 sampling 하여 coefficients of SH 로 이루어진 vector 를 leaf node 에 저장한다.

2.2.3. PlenOctree Optimization

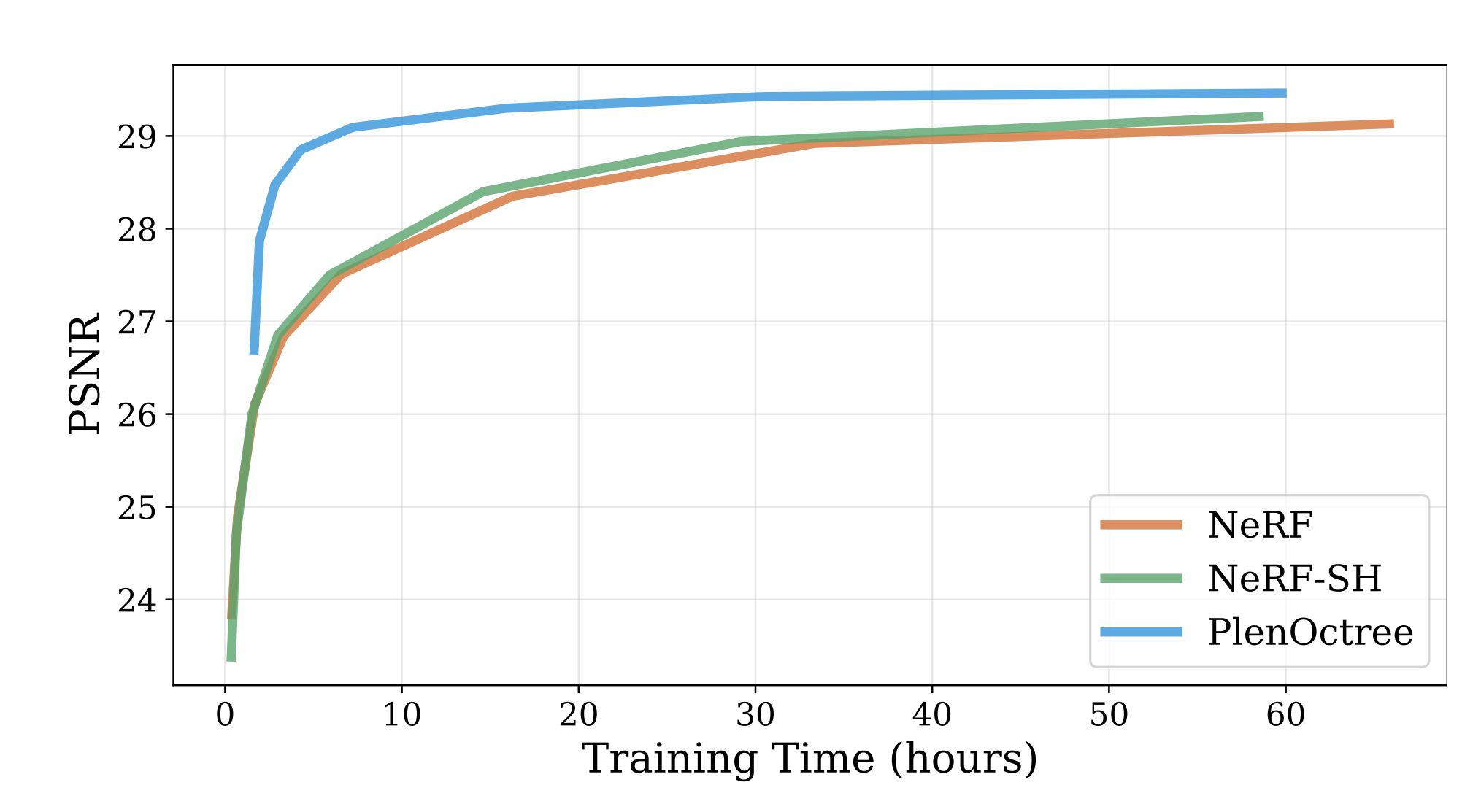
Volume rendering process 가 fully differenditble 하기 때문에, original NeRF loss 와 SGD 를 통해서 octree 를 directly optimize 할 수 있다고 한다. 이를 통해 일정 이상 NeRF 가 학습된 이후로는 octree 를 optimize 하는 것이 훨씬 빠르기 때문에 전체 pipeline 의 converge 를 original NeRF 대비 빠르게 끝낼 수 있다. 아래 실험에서 이를 확인할 수 있는데, NeRF 와 NeRF-SH 와 비교하여 훨씬 빠르게 학습되는 것을 알 수 있다.

3. Experiments

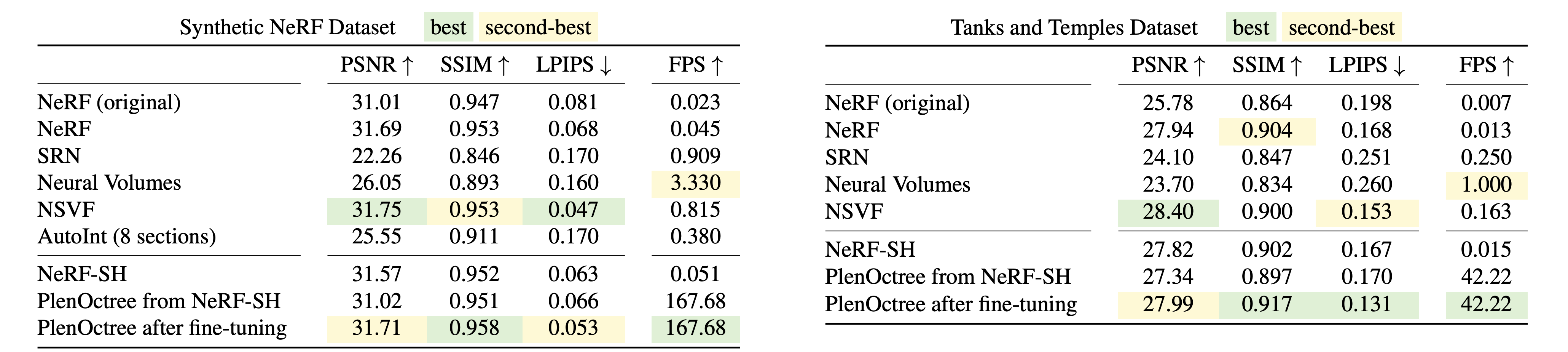
Qualitative, Quantitative results 모두 다른 baseline 비교해 near SOTA performance 을 보이면서 비교 불가능한 수준의 rendering 속도를 보여주는 것은 확실히 놀랍다. 비슷한 방식을 사용하는 NSVF 대비해서도 rendering rate 가 100배 이상 차이나는 것으로 보아 확실히 impressive 한 works 임은 틀림없다.

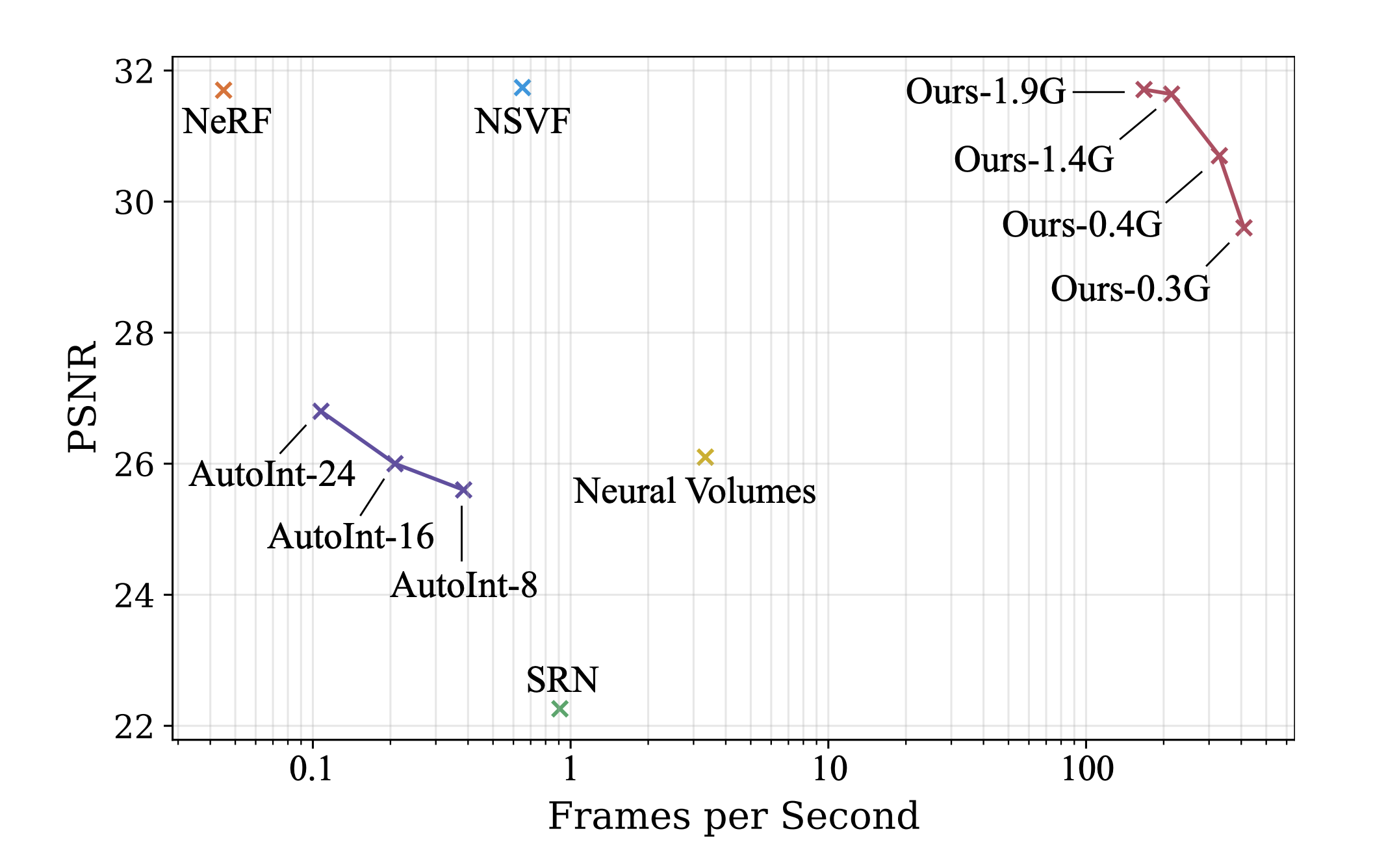
대신에 voxelize 시켜서 저장하게 되면 확실히 NeRF 의 특장점이었던 memeory efficiency 부분에서는 장점이 많이 퇴색되는 것이 보인다. NeRF 와 비슷한 성능을 위해서는 NeRF 의 ~5MB 와 비교해서 ~1.9GB 에 달하는 memory 를 점유하는 것을 알 수 있다.