[Review] TRADES: Theoretically Principled Trade-off between Robustness and Accuracy
DeepLearning_Paper_Review
이전까지 Adversarial Training 으로 학습된 Neural Network 는 vanilla training 에 비해서 accuracy 에서 성능 하락이 있는 것이 알려져 있었다, 즉 Robustness ↔ Accuracy 간의 Trade-off 가 존재한다. 이 논문은 이러한 Robustness ↔ Accuracy 간의 Trade-off 를 수학적으로 규명하고 이를 이용해 새로운 Adversarial Defense Algorithm: Trades 을 소개한다.
ICML2019
1. Introduction
1.1. Empirical Risk Minimization
논문에 본격적으로 들어가기에 앞서, Empirical Risk Minimization 에 대한 간단한 소개를 하도록 한다.
우리가 어떠한 loss function (or risk function ) 을 통해서 supervised learning 으로 Machine Learning Model 을 학습할 때, 이 학습의 loss (risk) 를 다음과 같이 정의할 수 있다.
여기서 는 ground-truth label 이고, 는 data 와 label 간의 Joint-Probability-Distribution 이다. 하지만 이러한 risk 는 다음 두 가지의 이유로 사용할 수 없다.
-
Computationally Intractable
-
Intractable Joint-Probability Distribution
그렇기 때문에 우리는 실질적으로는 training dataset 에서 sampling 된 risk 인 Empirical Risk
를 통해 model 을 학습해야하고, 이를 Empirical Risk Minimization (ERM)이라고 한다.
1.2. Adversarial Training with ERM
이제 ERM formulation 을 통해 Optimal Robust Training 을 다음과 같이 표현하자.
통상적인 supervised learning problem 에서 0-1 loss 는 우리가 학습을 통해 구하는 Estimator 가 maximun a posterior (joint probability) 가 되기 때문에 optimal loss 이다.
이를 통해 구할 수 있는 model 을 BayesOpt 라 하는데, 문제는 이 BayesOpt 를 구하는 방법이 np-hard problem 이라는 데 있다. (기본적으로 미분이 안되는 함수들은 최적화하기 굉장히 곤란하다)
따라서 0-1 loss 를 대체할 수 있는 surrogate loss 가 필요하고, 기존의 adversarial training 은 모두 이러한 surrogate loss 를 도입하여 adversarial training 을 진행하였다. 즉, 다음과 같은
min-max formulation 으로 나타나는 기존의 adversarial training 은 모두 이 0-1 loss 에 대한 surrogate loss 를 도입하여 training 을 진행한 것이다.
하지만 저자들은 이러한 formulation 이 실제 optimal risk 에 대한 tightest approximation 이 아니라고 주장하며, 이를 classification-calibrated loss 의 도입으로 differentiable tightest bound 를 구하여 도입한 새로운 Adversarial Training Algorithm 인 Trades 를 제시한다.
2. Preliminaries
2.1. Notations
-
Ball of Decision Boundary
Radius 가 인 norm ball 안의 (perturbed) 가 original input 과 다른 model output 을 도출하는 점이 존재. 즉, data point 근처에 Decision Boundary 가 있는 집합을 의미한다.
-
Conjugate function
이 함수는 에 대한 pointwise supremum of affine function 이기 때문에 원함수의 convex 여부에 상관없이 convex function 이다. 본 논문에서는 bi-conjugate 이 원함수에 대한 convex hull 을 만든다는 성질을 이용한다.
2.2. Robust Classification Error with Natural & Boundary Error
저자들은 ERM 학습에서의 error 를 다음과 같이 총 3개로 나누어서 정의한다.
-
Robust Error
Norm ball 내에서 neighborhood data 의 model output 이 ground-truth label 와 다른 경우의 error 이다. 학습된 model 이 얼마나 generalize 를 잘하는지를 나타내는 error 라고 보면 될 듯 하다.
-
Natural Error
Original data 의 model output 이 ground-truth label 과 다른 경우의 error 이다. (즉 True Negative)
-
Boundary Error
2.1. 의 Decision boundary set 정의에서 data point 의 norm ball 내의 decision boundary 위의 점 는 이다. 따라서 original model output 은 ground-truth label 과 같지만 perturbed data 에 대해 다른 output 을 내뱉는, 즉 adversarial attack 이 성공하는 경우의 error 이다.
각 3개의 error 의 정의를 통해 다음과 같은 관계를 도출할 수 있다.
- Robust Error : '잘못 배움' + 'perturbed 이후 DB 넘어감' 정도로 해석할 수 있겠다.
논문에서는 다음과 같은 Toy Example 에서 BayesOpt classifier (optimal estimator) 와 all-1 classifier (worst-case estimator) 에 대한 각각의 error 를 나타낸다.

.png)
즉, 위 예제에서조차 optimal estimator 라고 하더라도 robust error 를 0으로 만드는 것은 impossible 한 것을 알 수 있다.
3. Method
저자들은 위에서 제시한 robust error 와 natural error 등의 정의를 이용해 기존의 min-max formulation 으로 정의된 Adversarial Training 은 optimal objective 가 아님을 주장한다. 또한 Classification-Calibrated 를 통해 새롭게 정의되는 Adversarial Training 방법론을 제시한다.
3.1. Classification-Calibrated Loss
3.1.1. Optimal Risk & Good Classifier
Binary classification model 의 training risk 와 이의 하한을 다음과 같이 정의할 수 있다.
여기서 정의된 는 어떠한 training loss 로 구할 수 있는 최적의 estimator 에 대한 risk 임을 의미한다. 이를 통해 어떤 classifier model 의 Excess Risk 를 정의할 수 있다 .
- Excess Risk:이 값은 어떤 loss 에 대하여 현재 model 가 BayesOPT 와 얼마나 차이나는지를 의미한다.
또한 저자들이 인용한 'Convexity, Classification and Risk Boudns' 에서,
Good classifier 를 알맞은 예측을 50% 이상의 confidence 로 예측하는 classifier 라고 정의한다. 즉,
를 만족하는 classifier 가 good classifier 이다. confidence score of
3.1.2. Surrogate Risk with Confidence Score
0-1 loss 에 대한 surrogate loss function 를 통해 binary classification (predicted 와 GT label 의 곱이 1) 에 대한 surrogate loss 의 training risk 를 다음과 같은 Conditional risk 로 나타낼 수 있다.
- Conditional risk :
이를 이용하여 다음과 같은 함수를 정의할 수 있다.
- General Conditional risk : 이는 binary classification 에서의 confidence score 에 따른 risk function 이다.
여기서 가 에 대한 affine function 이고, 이 함수에 대한 infimum 을 다음과 같이 정의할 수 있다. (이는 affine function 의 infimum 이기 때문에 convex 이다.)
- Risk Infimum :이는 어떤 surrogate loss 에 대하여 prediction 가 정해졌을 경우, confidence 에 변함에 따라 risk 가 가질 수 있는 최저값을 의미한다. 이를 통해 우리는 optimal risk 를 risk infimum 을 이용하여 정의할 수 있다.
여기서 는 affine function 이기 때문에, affine function 의 infimum 인 는 convex 이다. 따라서 이 conditional risk 가 에서 최댓값을 가짐을 다음과 같이 보일 수 있다.
직관적으로는, 어떤 binary classifier 의 prediction 에 대한 확률이 50% (: coin toss classifier)일 때 risk 값이 최대임을 의미한다.
3.1.3. Classification-Calibrated
이제 Bad classifier (i.e. not Good Classifier) 를 다음과 같이 정의하자.
이를 통해 Bad Classifier 의 lower bound of conditional risk 를 다음과 같이 정의할 수 있다. (i.e., correct confidence score 가 50% 이하인 classifier : bad classifier 의 infimum)
Classification-Calibrated 는 다음과 같이 정의된다.
- Classification-Calibrated : 즉, 어떠한 surrogate loss 에 대한 risk 로 학습되는 classifier 에 대해,
Bad Classifier 의 lower risk bound > Good Classifier 의 lower risk bound
를 만족할 때 이를 Classification-Calibrated 라고 한다.
정의에 따라, classification-calibrated 를 만족시키는 surrogate loss risk 는 training 이 Bad Classifier -> Good Classifier 로 이루어질 것이기 때문에, Classification-Calibrated 는 good classifier 를 학습시킬 수 있는 좋은 surrogate loss 가 되어주는 기준이 된다.
3.1.4. Surrogate Loss Boundary Estimation
이제 surrogate loss 에 대한 다음과 같은 transformation 을 정의하자.
의 각 Risk infimum 의 input 은 의 input 을 받기 때문에, 이 transformation 은 어떠한 surrogate loss 에 대해 confidence 가 50% 이상인 prediction 에 대한 false prediction risk 와 positive prediction risk 의 차이를 의미한다.
이 transformation 는 다음과 같은 몇 가지 중요한 성질을 갖는다.
-
이기 때문에 이다.
-
transformation 은 bi-conjugate 임으로, 원함수의 tightest closed convex hull 이 되는데, 이에 따라 를 만족한다 (co : convex hull). 이는 convex 함수를 pointwise affine function 으로 나타낼 수 있기 때문이다. 따라서 는 convex function 이다.
-
Convexity 로부터, 인 에 대하여 를 만족하고, 이로부터 인 에 대해
이 성립한다. i.e. : non-decreasing 이므로 다음과 같이 는 non-decreasing 임을 알 수 있다.
다음은 binary classification problem 에서 classification-calibrated loss 의 몇 가지 예시이다.
.png)
3.2. Relating 0-1 loss to Surrogate Loss
위에서 정의된 transformation boundary 을 통해서 우리는 optimal robust training risk 의 bound 를 설정할 수 있다.
Transformation 을 통해, 어떠한 surrogate loss 로 정의되는 empirical excess risk 와 optimal excess risk 사이에 다음과 같은 inequality 가 성립한다.
이때 로부터,
를 만족한다. 위에서 제시된 inequality 를 이용하여 다음과 같은 식을 도출할 수 있는데,
이로부터 다음과 같은 upper bound, lower bound 를 유도할 수 있다.
-
Upper Bound
-
Lower Bound
특이할만한 점은 bound 를 설정함에 있어서 ground-truth label 이 필요하지 않다는 것이다. 또한 통상적인 min-max formulation 에서 볼 수 있는 adversarial attack 과도 조금 다른데, Robust classifier 의 tightest boundary 가 GT label 이 아닌, vanilla model 의 decision boundary 에만 관련이 있음을 알 수 있다.
3.3. Adversarial Training with Classification-Calibrated Bound
이제 기존의 Adversarial Training 과의 비교를 통해서 Trade-off Training 알고리즘을 설명한다.
-
Prior-Work :
기존 Adversarial training 에서는 inner-maximization problem 을 ground-truth label 과 adversarial example 간의 loss 를 이용해서 구했다.
-
TRADES
TRADES 는 natural error 와 decision boundary error 를 분리하여 <span style='color:red'decision boundary 에서의 maximization 을 통해 adversarial example 을 구하게 된다.
-
저자들은 제시하는 adversarial training 방법이 inner maximization 에서 label 이 필요하지 않으므로 semi-supervised setting에서 adversarial training 방법론으로써 쓰일 수 있다고 한다.
-
여기서 parameter 는 커질수록 BayesOpt, 작아질수록 all-one classifier 처럼 행동하게 될 것이다.
-
해당 값이 커짐에 따라 natural risk 만을 신경쓰는 BayesOpt 처럼 학습될 것이고, 작을수록 boundary risk 만을 신경쓰는 all-one-classifier 처럼 학습될 것이다. 즉 regulaizer 로써의 Trade-off coefficient 역할을 하게 된다.
-
2에서 제시된 optimization objective 를 이용한 학습 알고리즘은 다음과 같다.
.png)
주의할만한 점은 (7)에서 natural image 에 gaussian noise 를 더해주는 것이다. 이는 이미 학습이 끝난 classifier 는 seen data 에 대한 gradient 가 0에 가깝게 흐르기 때문이다. (local minima : )
4. Experiments
- 성능은 당시 기준 SOTA 이다.
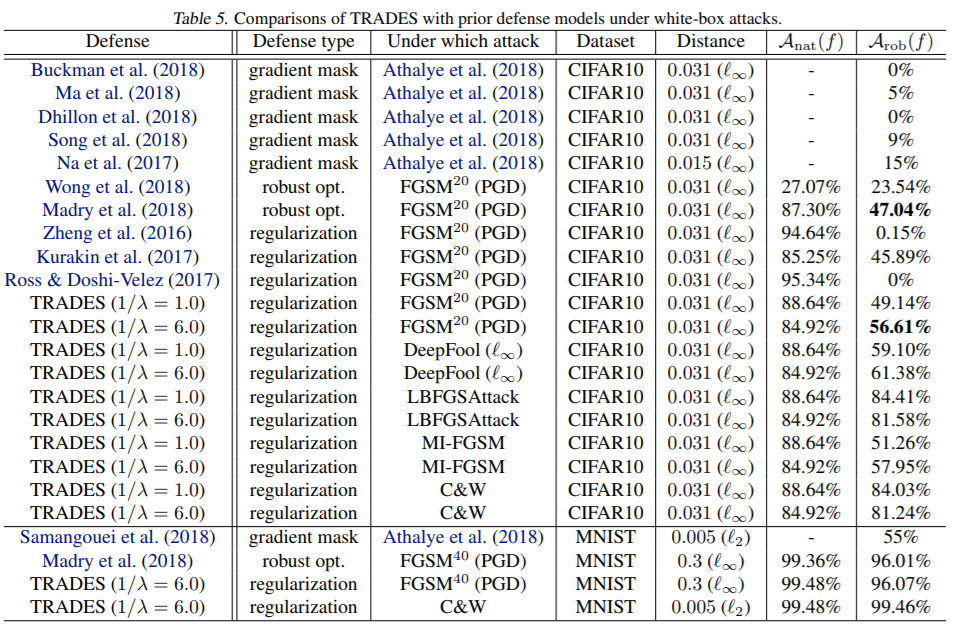
- 또한 parameter 에 따른 robust, natural error 변화도 report 되었다. 값이 커짐에 따라 natural error 가 작고, 작을수록 robust error 가 작음을 알 수 있다.

논문 자체보다는 인용한 논문인 'Convexity, Classification and Risk Boudns' 를 이해하는데 더 어려웠고, 실제로 convex optimization 에 익숙하지 않은 사람이 읽는다면 꽤 장벽이 있는 논문이라고 생각된다.
지금까지 Robust Traning 에서 accuracy 와 robustness 간의 trade-off 가 있다는 것이 알려진 것은 사실이지만, 이를 직접 수학적으로 규명하고 그러한 trade-off 가 필연적인 것임을 규명했다는 데 의의가 있다.
여담으로 FGSM 등과 비교하여 inner maximization 을 decision boundary error 로 접근했을 때 attack 의 성능 차이가 어떻게 되는지를 비교했으면 더 좋지 않았을까 하는 생각이 든다.
