CNN-based Object Detector 에서 NMS 나 anchor 등의 (Anchor-free 방식이 제시되긴 하였지만) 등의 hand-crafted processing 은 Detector 학습에 중요한 heuristic 적인 요소이다.
DETR 는 이러한 부자연스러운 prior knowledge 주입을 제거하고 object detection 을 end-to-end manner의 direct set prediction 으로 해결하는 방안을 제시하였다.
DETR: ECCV2020 oral
Preliminaries: Inductive Bias of Object Detection
a) Anchor Box
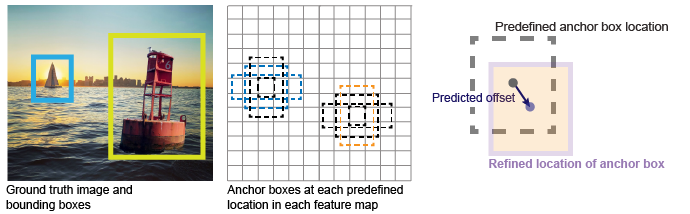
Fig: Anchor Method대표적인 object detection framework 는 anchor generation method 를 사용한다. Anchor box 는 각 feature map bin 에서 미리 정의된 크기와 개수의 box 들이 positive 인지 negative 인지 판별되고 이를 offset 으로 보정하여 최종적으로 localization 을 진행하게 된다. 자세한 내용은 이전 Free Anchor 리뷰를 참조:
- aspect ratio
- scale
- number of anchor
- etc....
하지만 위의 parameter 들은 heuristic manner 로 결정된다. (e.g. YoloV3는 k-means clustering 로 결정!)
Partial Solution : Anchor-Free Detector
Anchor-free Detector (CenterNet, CornerNet 등) 는 anchor 를 사용하지 않고 FPN feature map 에서 fixel-wise 로 objectness 를 판별하고 이에 대한 offset을 학습하여 bounding box 를 예측한다.
.png)
Fig: FPN feature map하지만 anchor-free detector 들은 anchor 를 사용하지 않는 대신 heuristic 하게 ground-truth bounding box 와 match 되는 기준을 세우는데, 가령 예를 들어 다음 식과 같이
크기가 작은 object 는 small feature map 에서, 큰 object 는 large feature map 에서 검출되게 되도록 설정된다.
즉 FPN-based anchor-free detector 는 사실 1-ratio, 5-scale anchor 와 본질적으로 크게 다르지 않 와다.
b) Non-Maximum Suppression
.png)
Fig: NMS algorithmNMS 는 post-processing method 로 한 class 내에서 highest confidence 를 갖는 box 를 고른 후, IoU 가 일정 기준 이상 넘는 다른 박스들을 삭제하는 방법이다.
- Overlap area metric : Intersection over Union
- Area threshold
하지만 이 또한 모두 heuristic manners 결정되며, 심지어 'IoU' 라는 기준 마저도 수학적이지 않다.
💡 대부분의 regression loss (L1 or SmoothL1) 는 주로 FP보다 FN을 낮추는 방향으로 강제된다. 즉, recall rate 가 1에 가깝게 학습된다.
이에 따라 NMS 를 사용하지 않을 경우 몇만개에 해당하는 proposal 을 output 으로 내뱉는다.
이는 anchor-free detectors (CornerNet & CenterNet) 에서도 해결되지 않은 문제이다. 따라서 거의 대부분의 Detector 들은 NMS 를 필수불가결한 과정으로 보았다.
1. Introduction
DETR 에서는 object detection 의 objective를 *set of bounding boxes and category labels 을 direct 하게 예측하는 것으로 정의한다. 즉 다음과 같이
Object Detector 를 정의할 수 있다.
기존 연구들은 이를 간접적인 regression (RPN), classification problems (Classification Head) 를 정의함으로써 해결하였지만, 저자들은 이러한 접근방식에는 preliminaries 에서 다룬 hand-crafted algorithm 이 필요하기 때문에 좋지 않다고 보았다.
따라서 부자연스러운 prior knowledge 주입을 제거하고 object detection 을 end-to-end manner의 direct set prediction 으로 해결하는 DETR framework 를 제시하였다.
2. Loss
2.1. Object Detection set prediction loss
DETR 에는 anchor 등이 존재하지 않아 feature map bin 과 GT 간의 matching 을 해주는 부분이 없기 때문에, 한 사진에서 output set 과 GT set 을 적절히 매칭시켜줄 필요가 있다.
DETR 는 Hungarian algorithm 을 이용하여 set prediction 에서의 optimal permutation 문제를 해결한다. (Hungarian algorithm 은 bipartite matching에서 polynomial time: 으로 solution 찾는 알고리즘이다. )
즉 다음과 같이 classification risk 와 regression risk 의 합으로 이루어진 matching cost 를 정의할 때,
DETR 가 추출한 output 과 GT 간의 permutation with a minimum cost 는 다음과 같은 optimization problem 으로 정의된다.
위의 bipartite matching problem 을 Hungarian algorithm 을 통해 해결하며, 구해진 permutation 은 전체 loss 를 구하는데 활용되게 된다.
- 여기서 는 fixed-length () vector 이며, 은 통상적인 image 안에서 object 수보다 훨씬 큰 수로 정의되어 있다. ground-truth label 은 크기에 맞춰 'no-object token' 로 padding 된다.
Entire Hungarian loss :
matching cost 와 다른 점은 negative log probability 를 사용한다는 점이다. 이는 class prediction term 이 regression loss 와 commensurable 하게 한다. (성능도 더 잘나온다고 한다.)
- Background(no-object) class imbalance 문제를 해결하기 위해서 no-object 에 대해서는 pre-defined factor (10) 으로 cost 를 나눠주었다.
💡 Class prediction 에서 no-object class 는 다른 object detection 에서의 background class 와 같은 역할이다. COCO dataset 에서 object detectors 는 일반적으로 81 classes 로 학습되는데, 이는 80 COCO class 에 background class 를 하나 더한 것이다.
DETR 에서는 AP score를 올리기 위해서, prediction 의 highest confidence가 no-object 일 경우, second-highest confidence class 로 대체하여 AP metric 을 계산했다고 한다.
2.2. Regression Loss
'Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression' (CVPR2019), 에서 제시된 Generalized IoU 를 일부 수정하여 regression loss 를 사용하였다.
Generalized IoU 는 partially modified version of IoU 로, IoU 값이 0 일 때에도 서로 다른 두 box 를 가깝게 할 수 있다. (IoU 는 값이 0 일 때에는 두 box 가 가까운지 먼지 상관없이 고정된다)
식을 살펴보면 GIoU 가 -1 에서 1 사이로 정의된다. 따라서 IoU loss 는 0과 2사이의 값을 갖는다. 이를 전통적인 L1 loss 와 합쳐서 최종 regression box 는 다음과 같이 정의된다.
.png)
Table: Loss Abaltion위의 ablation study table 을 통해 regression loss 의 각 요소가 성능 향상에 큰 도움이 되는 것을 알 수 있다.
3. DETR architecture
.png)
Fig: Overall architecture of DETRDETR 는 set prediction 을 위해서 Transformer architecture 를 사용했다. 최근 vision task 에서도 ViT 나 Swin Transformer 등에서 transformer 가 각광받고 있다.
저자들이 object detection 을 direct set prediction 으로 풀려고 노력했기 때문에 NLP 등에서 사용되던 self-attention-based architecture 를 차용한 것으로 보인다. 이러한 구조들은 sequence (set) input-output 처리에 강점이 있는 것으로 알려져있다.
구체적으로는 CNN (ResNet-50)으로 이루어진 feature extractor 와, transformer 로 이루어진 set predictor 로 구성되어 있다. ViT 등의 stand-alone visual attention model 과 다르게 convolution 을 통해서 visual feature 를 추출한 후 이를 이용하게 된다.
💡 ViT에서 Transformer 는 Visual Tasks 에 특화되지는 않는 것으로 드러났다. (ImageNet 1K만으로는 성능이 좋지 않음). 그보다는 대량의 데이터로부터 inherent inductive bias 를 배우기에 능하다고 해석하는 것이 좋다. 즉 object detection 에서도 대용량의 데이터가 존재한다면 feature extractor 부터 stand-alone transformer 로 구성된 architecture 가 좋은 성능을 보일 수 있을 것이다.
3.1. Encoder
Encoder stage 에서, DETR 는 multi-head self-attention 을 수행한다.
- Self-attention 특유의 large computational cost 때문에 CNN에서 추출된 feature map 을 바로 쓰지 않고 channel dimension reduction 을 (1x1 Conv) 수행한 뒤 적용시킨다.
특히, original transformer 처럼 fixed sinusoidal positional encoding 이 input 에 추가되어 self-attention 연산을 수행한다. 이는 permutation-invariant 한 self-attention 에 location information 을 추가해주는 것이라고 해석할 수 있다. (Fourier Featuring Review)
.png)
- 위 그림은 positional encoding 을 시각화 한 것인데, k 값에 따라 주기의 길이가 비례하여 길어지는 것을 볼 수 있다.
- Transformer 에서는 NLP task 특성상 max length 가 정해져 있고, DETR 에서는 image 를 일괄적으로 resize 하여 처리하기 때문에 feature map 크기가 같다. 즉 식에서 m 의 크기는 고정된다.
여기서 positional encoding 은 단위원을 회전하는 점 좌표의 집합으로 정의한 것을 알 수 있다.
이는 relative position 표현에 대한 이점을 가지는데, 원 위의 두 점 사이의 relative position 이 오일러 공식 () 을 통해 간단하게 표현될 수 있으며, 따라서 같은 relative position 을 가지는 feature 간의 관계가 고정 된다. 이는 relative position 을 attention 에서 훨씬 쉽게 학습하는 효과를 지닌다고 한다. 다음을 보자.
이때 각각 real, imaginary coefficient 가 좌표평면 상의 좌표를 나타내기 때문에 이를 다음의 Matrix-Vector multiplication 으로 나타낼 수 있는데,
이에 따라 relative position 을 나타내는 선형 변환이 모두 같은 rotation matrix 로 표현되는 것을 알 수 있다.
DETR 에서는 상기 encoding의 2D coordinates extended version 을 사용한다. 2D positional encoding 은, sinusoidal function 이 x, y-axis 에 각각 개별적으로 적용된 뒤 concat 되는 구조이다.
.png)
위 그림을 통해 symmetric 한 distance 를 유지하면서 relative position 에 따라 변하는 positional encoding 값을 볼 수 있다.
3.2 Decoder & Feed-Forward Network
.png)
Fig: Detailed Transformer architecture of DETRDecoder stage 에서 DETR는 embeddings of size 을 object query 로 하여 (encoder 에서의 positional encoding 과 같은 역할) multi-head self-attention 을 수행한다. Original Transformer 와 다르게 각 decoder layer 에서 decodes the objects in parallel 한다.
여기서 object query 는, random initialize 된 개의 object location 이다. Training 과정에서 update 되며 evaluate 시 고정된다. 이는 DETR 가 image query 를 통해서 prediction을 할 때 같은 영역을 보지 않도록 동작 하게 만든다.
아래 그림은 COCO dataset 에서 학습된 learned embedding 의 visualization 결과이다. 전체적으로 image 영역에 uniformly 하게 분포됨을 알 수 있다.
.png)
Fig: Visualization of learned embedding of DETR's decoder각 image query 들은 독립적으로 decoded 되어 box coordinates 와 class labels 을 예측하는 Feed-Forward-Network 로 넘어간다. FFN 은 다음 두 가지 prediction 을 동시에 수행한다.
- Normalized center coordinates, height, and width of the box :
- Class label using a softmax function (in linear layer)
4. Experiments
4.1. Quantitative Analysis: Main Table
.png)
Table: Comparison with RetinaNet and Faster R-CNN on COCO. 전체적으로 DETR 는 Faster-RCNN 에 준하는 성능을 보여주고 있다. Faster-RCNN 보다 large objects 영역에서 웃도는 성능을 보이지만, small objects 에서는 훨씬 뒤쳐지는 성능이다. 이는 Transformer architecture 를 Visual Task 에 적용했을 때 일반적으로 드러나는 특징인데, self-attention 의 computation cost 문제로 channel 수나 feature map size 를 일반적인 CNN 에서보다 훨씬 작게 사용하는 경향이 있기 때문이라고 생각한다.
⚠️ 언급된 구현 디테일 중에 augmentation technique 이 눈여겨 볼만하다. DETR 에서는 original image 를 random crop 한 후, cropped bbox 를 GT bbox 와 비교하여 일정 이상의 영역이 제거됐다면 이의 annotation 을 제거하는 augmentation 을 사용하였다.
Object detection 은 그 특성상 bounding box location 이 바뀌는 augmentation 을 구현하기 쉽지 않은데, 간단한 방식으로 효과적인 box location augmentation 을 적용하였다. 이에 대한 성능 향상도 꽤 높은 편. (about 1mAP)
4.2. Quantitative & Qualitative Analysis: Encoder
.png)
Fig: Encoder self-attention for a set of reference points..png)
Table: Effect of encoder size.또한 위 Table 에 의하면 Encoder 수가 성능에 밀접한 영향을 끼치는 것을 알 수 있다. 그리고 각 개별 Encoder 가 image 내에서 individual instances 를 구별할 수 있는 것으로 보인다. (논문에서는 Faster-RCNN → Mask-RCNN 처럼 head 만 변경하여 panoptic segmentation 으로 확장가능함을 보여주었는데, encoder 의 이러한 능력에서 착안한 실험인 것 같다.)
💡 Encoder 수의 중요함에 대해서는 이미 'Attention is all you need' 에서 다뤄진 바 있다. Orignal Transformer 에서는 attention block 을 multi-heads 로 구성했을 때, 각 head 가 각기 다른 관점에서 data 를 'attention' 할 수 있다고 주장했다. 즉 일정 개수 이하의 encoder 로는, 데이터의 풍부한 feature 를 얻을 수 없기 때문에 attention 품질이 떨어지게 될 것이다.
4.3. Quantitative & Qualitative Analysis: Decoder
.png)
Fig: Visualizing decoder attention for every predicted object. 위 그림에서는 Decoder layer 의 중요성을 알 수 있다. Decoder 는 encoder 와 다르게 개별 instance 의 detail 에 치중하는 경향을 보인다. 이때 decoder layer 수가 충분하지 않다면 output elements 간의 cross-correlation 을 판단하는 능력이 떨어지고, 일반적인 RPN처럼 다량의 False Positive prediction 을 생성할 수 있다고 주장한다.
이런 직관에 착안하여 Decoder layer 갯수에 따른 NMS 적용시의 성능 변화를 제시한다.
.png)
Decoder layer 수가 증가할수록 각 decoder 가 output 간의 correlation 을 분간하고 중복된 prediction 을 방지하게 되며, False Positive Prediction 을 제거 하게 된다고 주장한다. Decoder Layer 수가 적을 때에는 NMS 를 적용했을 때 성능이 차이나지만, 그 수가 증가함에 따라 점차 NMS 와의 차이가 옅어진다. 이에 따라 DETR framework 는 NMS post-processing 의 필요성을 효과적으로 제거했다고 볼 수 있다.
5. Conclusion
DETR 는 end-to-end manner 로 object detector 를 학습하는 방법을 효과적으로 제시하였다. 이는 OD 를 direct set prediction problem 으로 간주하고 Transformer Architecture 를 차용하여 이루어진 결과로, hand-crafted prior knowledge 를 제거하고도 Faster-RCNN 과 비슷한 성능을 보여주는 것을 실험적으로 규명하였다.
Small objects 에서의 성능은 상대적으로 부족하지만, large object detection 에서는 Faster-RCNN 보다도 훨씬 뛰어는 성능을 보여준다. 또한 DETR 는 panoptic segmentation 등의 task 로 확장이 Head 만 바꿔서 이루어지는 식으로 쉽게 이루어지는 것을 보여주었다.
