기본 개념 정리

• 집합 : 우리과 관심있어 하는 수학적 대상(수, 함수, 집합)의 모임

• 멱집합 : 해당 집합의 모든 부분집합을 포함하는 집합
  (공집합부터 시작해서 모든 조합을 포함한 집합이 멱집합)

  S={A,B,C}
  P(S)={∅,{A},{B},{C},{A,B},{A,C},{B,C},{A,B,C}}

대수 구조

대수(Algebra) = 수와 기호를 이용해 연산을 연구하는 학문
구조 = 집합 + 연산

대수 구조 (대수 + 구조 + 8개의 공리) : 집합, 연산이 만족시켜야하는 조건 = 벡터공간

공리 : 조건(명제)

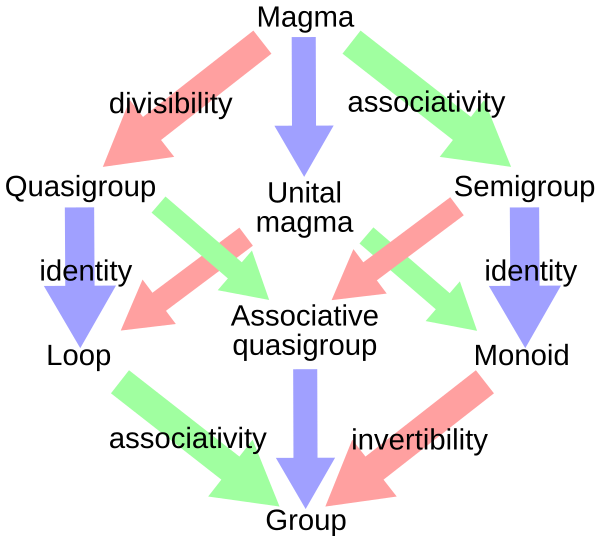
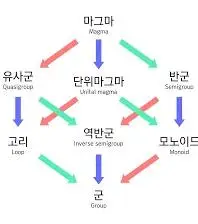
마그마(Magma)

마그마(Magma) : 집합 S에 이항연산(+)이 정의된 대수 구조

즉, 집합 S의 두 원소를 연산(+)하면 다시 집합
S의 원소가 나오는 구조를 의미해. 이걸 수학적으로 "닫혀 있다"고 표현해.

집합 S의 두 원소를 연산(+)하면 다시 S 안에 있는 원소가 나온다는 거야.

군(group)

군(Group) : 집합과 이항연산이 주어진 대수 구조 중에서 특정 조건을 만족하는 구조.

군(group)의 3가지 필수 조건

1. 결합법칙(Associativity) → "반군(Semigroup)"

(a+b)+c=a+(b+c)

✅ 연산의 순서를 자유롭게 바꿀 수 있다는 뜻.
✅ 하지만 괄호만 바꿀 수 있고, 위치(교환법칙)는 바꾸지 못함.
✅ 결합법칙만 만족하면 반군(Semigroup)이라고 불른다.

2. 항등원(Identity Element) → "모노이드(Monoid)"

a+e=a

✅ 어떤 원소 e가 있어서 어떤 원소와 연산해도 값이 변하지 않으면 "항등원".
✅ 항등원이 존재하면, 반군 + 항등원 = 모노이드(Monoid)

• 예시

a+0=a
a×1=a
A⋅I=A

3. 역원(Inverse Element) → "군(Group)"

a+x=0,x=−a

✅ 각 원소마다 "역원"이 존재해야 한다.
✅ 즉, 어떤 원소를 더해서(연산해서) 항등원이 나오면, 그 원소는 역원이다.
✅ 항등원이 있고, 역원이 존재하면 모노이드 + 역원 = 군(Group)

아벨 군 (Abelian Group, 가환 군)

아벨군 = 군(group) + 교환법칙

a+b=b+a

환(ring)

환(Ring): 두 개의 연산(덧셈, 곱셈) 이 정의된 대수 구조 ex) 1.(R,+,x), 2.(Z,+,×), 3.(Q,+,×)

호

1. 덧셈 연산 → "가환군(Abelian Group)"

   ✅ 덧셈의 결합법칙: (a+b)+c=a+(b+c)
   ✅ 덧셈의 항등원(0) 존재: a+0=a
   ✅ 덧셈의 역원(음수) 존재: a+(−a)=0
   ✅ 덧셈의 교환법칙(가환성): a+b=b+a

2. 곱셈 연산 → "모노이드(Monoid)"

   ✅ 곱셈의 결합법칙:(a×b)×c=a×(b×c)
   ✅ 곱셈의 항등원(존재할 수도 있고, 없을 수도 있음)
   ❌ 역원(나눗셈)은 필요 없음:a×1=a

3. 분배법칙(아벨군과 차이점)

   ✅ 왼쪽 분배법칙: a×(b+c)=(a×b)+(a×c)
   ✅ 오른쪽 분배법칙: (a+b)×c=(a×c)+(b×c)

✅ 환에서는 곱셈이 덧셈을 어떻게 다루는지가 중요함!

체(field)

체(Field) : 환(Ring)의 성질을 만족하면서 곱셈의 역원이 있어야 함.

(1) 덧셈 구조 → 가환군(Abelian Group)

• 체의 덧셈은 가환군을 이루어야 함.

(2) 곱셈 구조(환과 차이점) → 가환군(Abelian Group, 0 제외)

환과의 차이점이 바로 여기 있음!
체에서는 0을 제외한 모든 원소가 곱셈의 역원을 가져야 함.

✅ 곱셈의 역원 존재 (0 제외)- 링과 차이점

$a \times a^{-1} = 1, \quad a \neq 0$

실수체 복소체

• 실수체:실수 집합 R에서 덧셈과 곱셈이 체(Field)의 조건을 만족하는 구조를 실수체(Real Field)
  $(R,+,×)$

• 복소체:복소수 집합 C에서 덧셈과 곱셈이 체(Field)의 조건을 만족하는 구조를 복소체(Complex Field) $(C,+,×)$

복소수 : 복소수는 실수와 허수 𝑖 를 포함하는 수의 집합.

$C={a+bi∣a,b∈R,i^{2}=−1}$

정리

체	원소	곱셈 역원 존재?	체 여부
실수체 $\mathbb{R}$	실수 ( a )	$a^{-1} = \frac{1}{a},\quad a\neq 0$	✅
복소체 $\mathbb{C}$	복소수 ( a + bi )	$(a + bi)^{-1} = \frac{a - bi}{a^2 + b^2}$	✅

벡터공간

벡터들이 모인 집합 V, 스칼라가 모인 체 F(실수체, 복소수체)

$+ : V \times V -> V$

$+ : F \times V -> V$

$(V,F,+,*) = Module(Ring)$

벡터공간: 벡터합에 아벨 군 4개 + 스칼라곱에 대한 성질 2 개 + 분배 법칙 2개 = 총8개 공리

공간

내적 공간

내적 공간 : 실수체 또는 복소수체 벡터공간에 내적을 추가한 구조

내적을 활용하여 놈(Norm), 거리(Metric), 위상(Topology)을 차례로 정의할 수 있음.

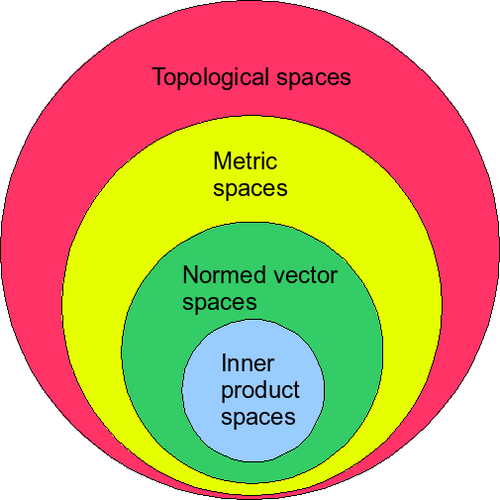
참고: 위상 = 열린 집합(open set)의 모임

---

1. 벡터공간 → 내적 공간

✅ 벡터공간(Vector Space)

• 실수체 $\mathbb{R}$ 또는 복소수체 $\mathbb{C}$ 위에서 정의된 벡터들의 집합.
• 벡터 덧셈과 스칼라 곱 연산이 존재.

✅ 내적(Inner Product) 추가

• 두 벡터 간의 관계를 수치(스칼라)로 정량화하는 연산.
• 예: 유사도 측정, 직교(orthogonality) 판별 등
• 두 벡터의 내적이 0이면 직교(수직).
  $\mathbf{u} \cdot \mathbf{v} = 0 \quad \Rightarrow \quad \mathbf{u} \perp \mathbf{v}$

✅ 내적 공간(Inner Product Space)

• 벡터공간에 내적을 추가한 구조.
• 내적의 예시:
  • 유클리드 내적:
    $\mathbf{u} \cdot \mathbf{v} = u_1 v_1 + u_2 v_2 + \dots + u_n v_n$
  • 복소 내적: $\langle \mathbf{u}, \mathbf{v} \rangle = u_1 \bar{v_1} + u_2 \bar{v_2} + \dots + u_n \bar{v_n}$

---

2. 내적 공간 → 놈 공간

✅ 놈(Norm) 정의

• 내적으로부터 벡터의 크기(길이)를 정의할 수 있음.
• 놈(Norm): $\|\mathbf{v}\| = \sqrt{\langle \mathbf{v}, \mathbf{v} \rangle}$
• 놈을 통해 벡터의 길이 및 크기를 계산할 수 있음.

✅ 놈 공간(Normed Space)

• 내적에서 유도된 놈을 가진 공간.
• 벡터의 크기를 정의할 수 있으므로, 크기 비교 및 거리 개념을 도입할 수 있음.

---

3. 놈 공간 → 거리 공간

✅ 거리(Metric) 정의

• 놈을 사용하여 벡터 간의 거리를 정의할 수 있음.
• 거리 함수 (Metric):
  $d(\mathbf{u}, \mathbf{v}) = \|\mathbf{u} - \mathbf{v}\|$
• 유클리드 거리(일반적인 거리 개념)와 연결됨.

✅ 거리 공간(Metric Space)

• 거리 개념이 존재하는 공간.
• 벡터 간의 "가까움"을 정의할 수 있음.

---

4. 거리 공간 → 위상 공간

✅ 위상(Topology) 정의

• 거리 개념이 있으면 열린 집합(open set)을 정의할 수 있음.
• 열린 집합을 통해 위상적 성질(연속성, 수렴 등)을 연구 가능.

✅ 위상 공간(Topological Space)

• 거리에서 유도된 위상을 가지는 공간.
• 함수의 연속성, 수렴성 등을 연구하는 공간.

---

5. 전체 구조 흐름 정리

벡터공간에 내적을 추가하고, 이를 점진적으로 확장하여 거리와 위상을 정의하는 과정:

1. 벡터공간 (Vector Space)

   • 벡터 덧셈과 스칼라 곱 연산이 가능한 공간.

2. 내적 공간 (Inner Product Space)

   • 내적(Inner Product)을 추가하여 벡터 간의 유사도 및 직교성을 정의.

3. 놈 공간 (Normed Space)

   • 내적으로부터 놈(Norm)을 정의하여 벡터의 크기(길이)를 측정할 수 있는 공간.

4. 거리 공간 (Metric Space)

   • 놈으로부터 거리(Metric)를 정의하여 벡터 간의 거리 개념을 도입.

5. 위상 공간 (Topological Space)

   • 거리로부터 열린 집합(Topology)을 정의하여 연속성과 수렴성을 연구할 수 있는 공간.

즉, 각 개념이 다음과 같이 확장됨:

$\text{벡터공간} \quad \Rightarrow \quad \text{내적 공간} \quad \Rightarrow \quad \text{놈 공간} \quad \Rightarrow \quad \text{거리 공간} \quad \Rightarrow \quad \text{위상 공간}$

---

6. 정리

공간	정의 요소	설명
벡터공간	벡터 덧셈, 스칼라 곱	벡터 연산이 가능한 기본 공간
내적 공간	벡터 내적	벡터 간의 유사도, 직교성 정의
놈 공간	벡터 놈 (길이)	벡터의 크기를 측정 가능
거리 공간	벡터 거리 (Metric)	벡터 간의 거리 개념 추가
위상 공간	열린 집합 (Topology)	연속성, 수렴성 연구 가능

---

7. 결론

• 벡터공간에서 출발하여, 내적을 추가하면 내적 공간이 생성됨.
• 내적으로부터 놈을 정의하면 놈 공간이 되고, 거리 개념을 도입하면 거리 공간이 됨.
• 거리로부터 열린 집합을 정의하면 위상 공간이 됨.

차원과 기저

$V = ( \mathbb{R} \time \mathbb{R} = \mathbb{R}^{2},+,*)$

$v \in \mathbb{R} \times \mathbb{R} \Rightarrow v = (x, y)$

$\beta = \{(1,0), (0,1)\} \Rightarrow \dim V = |\beta| = 2$

벡터 공간의 차원의 정의: 벡터 공간의 기저(basis, 집합)의 원소의 개수

벡터 공간의 기저: 벡터 공간의 부분 집합으로 선형 독립이고 공간을 생성한다.

그렇다면 모든 벡터 공간에는 기저가 있을까? Yes

$v = (1,2,3) \Rightarrow \dim V = 3$

$M_{2 \times 2} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \iff m = (1,2,3,4) \in M \Rightarrow \dim M = 4$

넘파이의 reshape은 벡터 공간의 차원을 보존한다.

넘파이 차원 = 수학의 텐서의 차수, 랭크

유클리드 공간(벡터공간)

RR^n = overbrace(RR xx RR xx cdots xxRR)^n

(1, 2, 3) in RR^3 => dim RR^3 = 3

(1, 2, 3, 4) in RR^4 => dim RR^4 = 4

a, b, c, d in RR, M_(2xx2) = [a, b; c,d] => (M_(2xx2), RR, +, *) 

M_(2 xx 2) ~=RR^4 <=> dim M_(2xx2) = dim RR^4 = 4

beta = { 
[1, 0;0, 0], [0, 1;0, 0], [0, 0;1, 0], [0, 0;0, 1] 
} "(기저)"

[a, b;c,d] = a[1, 0;0, 0] + b[0, 1;0, 0] + c[0, 0;1, 0] + d[0, 0;0, 1] "(선형결합으로 생성)"

<=> span(beta) = M_(2xx2)

a[1, 0;0, 0] + b[0, 1;0, 0] + c[0, 0;1, 0] + d[0, 0;0, 1] = [0, 0; 0, 0]

<=> a = b = c = d = 0 "(선형독립)"

|beta| = 4 = dim M_(2xx2) 

과연 유클리드 공간의 스칼라 체는 무엇일까?

어떤 벡터 공간의 스칼라 체가 F이고 차원이 n이라면 이 벡터 공간은 F^n과 동형일까

dim M(RR)_(2xx2)= 4 => M(RR)_(2xx2) ~= RR^4