1) 트랜스포머(Transformer)
-
트랜스포머 : 2017년 구글이 발표한 논문인 "Attention is all you need"에서 나온 모델로 기존의 seq2seq의 구조인 인코더-디코더를 따르면서도, 논문의 이름처럼 어텐션(Attention)만으로 구현한 모델. RNN을 사용하지 않음. 성능은 RNN보다 우수하다
-
Attention : 특정 정보에 좀 더 주의를 기울이는 것
- ex. 번역 : “Hi, my name is minsu.” -> “안녕, 내 이름은 민수야.”
- '이름은' 이라는 토큰은 디코드할 때 가장 중요한 것은 'name'
- “Hi, my name is minsu.” 에서 모든 토큰이 비슷한 중요도를 갖기 보단 'name'이 더 큰 중요도를 갖게 하고 싶음
1. 기존의 seq2seq 모델의 한계
- 인코더가 입력 시퀀스를 하나의 벡터로 압축하는 과정(고정된 크기의 컨텍스트 벡터를 만드는 과정)에서 입력 시퀀스의 정보가 일부 손실(기울기 소실)
-> 어텐션으로 개선 - 연산속도가 느림 -> 어텐션만으로 인코더와 디코더를 만듬 (트랜스포머)
2. 트랜스포머(Transformer)의 주요 하이퍼파라미터
- dmodel : 트랜스포머의 인코더와 디코더에서의 정해진 입력과 출력의 크기. 임베딩 벡터의 차원 (논문에서는 dmodel = 512)
- num_layer : 인코더와 디코더가 총 몇 층으로 구성되었는지 (논문에서는 각각 6개씩 쌓음)
- num_heads : 병렬의 개수. 어텐션을 여러개로 분할하여 병렬로 수행하여 결과값을 다시 하나로 합침. (논문 : 8)
- dff : 피드 포워드 신경망의 은닉층의 크기. (2048) (피드포워드의 입출력층의 크기는 dmodel)
3. 트랜스포머(Transformer)
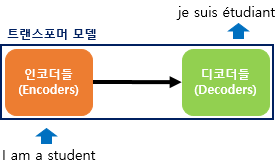
- RNN (x)
- 인코더-디코더 구조 : 인코더에서 입력 시퀀스를 입력받아 디코더에서 출력 시퀀스를 출력
- 차이점 : seq2seq는 각각 하나의 RNN이 t개의 시점을 가지는 구조였으면 트랜스포머는 인코더-디코더 단위가 N개 존재할 수 있다.
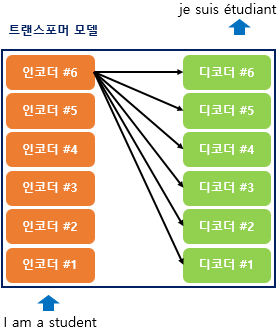
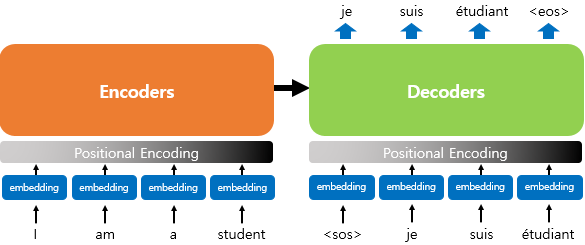
- 인코더와 디코더가 6개씩 존재하는 트랜스포머의 구조
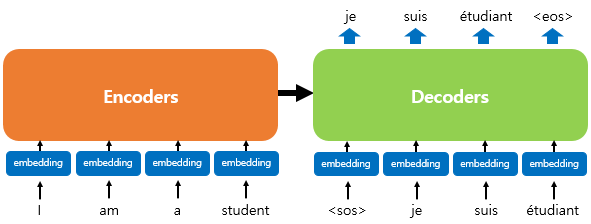
- 인코더-디코더의 구조를 유지 : 시작 심볼 <sos>, 종료 심볼 <eos> 사용
4. 포지셔널 인코딩(Positional Encoding)
- 트랜스포머는 RNN과 달리 순차적 입력이 아니라 단어의 위치 정보를 알려줘야함.
- 포지셔널 인코딩 : 각 단어의 임베딩 벡터에 위치 정보들을 더하여 모델의 입력으로 사용 (상대적 위치)
- ※ RNN은 단어의 위치에 따라 단어를 순차적 입력 받아 위치정보를 가져 자연어처리에 유용하다

-
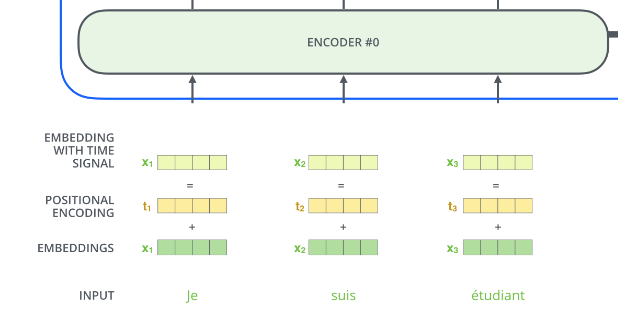
인코더의 입력 = 임베딩 벡터 + 포지셔널 인코딩 값
-
포지셔널 인코딩?
.png)
-
pos : 입력 문장에서의 임베딩 벡터의 위치 (단어의 위치)
-
i : 임베딩 벡터 내의 차원의 인덱스
- 어떤 특정 두 토큰의 위치값이 동일해질 수 있는 것을 방지. 동시에 사용하면 값들을 일정하게 증가/감소하게 표현할 수 있다. (참고)
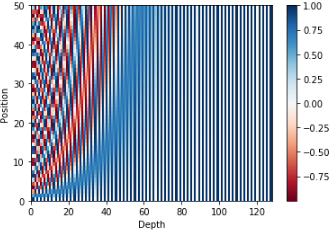
- 차원에 갯수에 따라 사인/코사인 그래프가 달라진다.
- 벡터의 차원에 따라 frequency가 줄어듦(sin/cos의 주기가 길어짐)을 알 수 있다. 따라서 파장에서 2π에서 10000*2π까지의 값을 갖는다
-
dmodel : 트랜스포머 모든 층의 출력 차원 (그림에서는 4 실제 논문에서는 512)
-
주기가 10000^(2i/dmodel)*2π인 삼각 함수
- i에 0부터 dmodel/2 까지 대입해 dmodel차원의 포지셔널 인코딩 벡터를 얻음
- i가 짝수일 경우 사인 함수의 값을 사용, 홀수일 경우 코사인 함수의 값을 사용
- pos 마다 이 값을 구하면 같은 column이라도 pos가 다르면 다른 값을 가짐
- = pos 마다 다른 pos와 구분되는 포지셔널 인코딩 값을 구할 수 있다
- = 각 임베딩 벡터에 포지셔널 인코딩값을 더하면 같은 단어더라도 문장 내 위치에 따라 트랜스포머의 입력으로 들어가는 값이 달라진다.
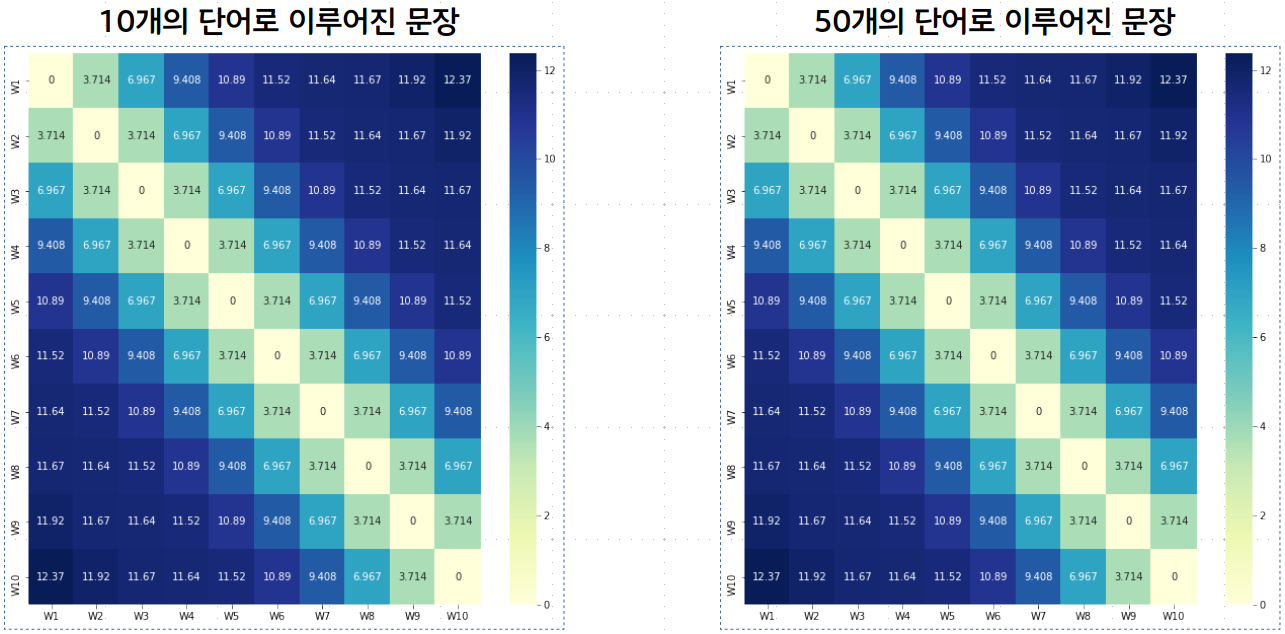
- 문장에서 단어의 위치마다 하나의 유일한 값을 가져야함.
- 서로 다른 길이의 문장에서도 두 단어 간의 거리가 일정해야함
- 더 긴 문장이 나왔을 때 적용될 수 있어야함 (값이 일정한 범위 안에 있어야함) - 정수 인코딩X
- 매번 다른 값이 나오면 안됨. 하나의 key 값처럼 결정되어야 함. - 임의의 범위를 정해서 그 안에서 나누는 것X
-
단어 순서대로 정수 값(1, 2, 3, 4)으로 인코딩하는 경우
-
상대적 거리(1)는 표시할 수 있지만 두번째 문장과 같이 문장의 길이가 매우 큰 경우는 토큰 값이 매우 커짐 -> 원래의 임베딩 벡터의 값에 영향을 줌 -> 범위 안에서 인코딩함
“어머님 나 는 별 하나 에 아름다운 말 한마디 씩 불러 봅니다”
“소학교 때 책상 을 같이 했 던 아이 들 의 이름 과 패 경 옥 이런 이국 소녀 들 의 이름 과 벌써 애기 어머니 된 계집애 들 의 이름 과 가난 한 이웃 사람 들 의 이름 과 비둘기 강아지 토끼 노새 노루 프란시스 쟘 라이너 마리아 릴케 이런 시인 의 이름 을 불러 봅니다”
1: ‘어머님’, 2: ‘나’, 3: ‘는’, 4: ‘별’, 5: ‘하나’, 6: ‘에’, 7: ‘아름다운’, 8: ‘말’, 9: ‘한마디’, 10: ‘씩’, 11: ‘불러’, 12: ‘봅니다’
1: ‘소학교’, 2: ‘때’, 3: ‘책상’, 4: ‘을’, 5: ‘같이’, 6: ‘했’, 7: ‘던’, 8: ‘아이’, 9: ‘들’, 10: ‘의’, 11: ‘이름’, 12: ‘과’, 13: ‘패’, 14: ‘경’, 15: ‘옥’, 16: ‘이런’, 17: ‘이국’, 18: ‘소녀’, 19: ‘들’, 20: ‘의’, 21: ‘이름’, 22: ‘과’, 23: ‘벌써’, 24: ‘애기’, 25: ‘어머니’, 26: ‘된’, 27: ‘계집애’, 28: ‘들’, 29: ‘의’, 30: ‘이름’, 31: ‘과’, 32: ‘가난’, 33: ‘한’, 34: ‘이웃’, 35: ‘사람’, 36: ‘들’, 37: ‘의’, 38: ‘이름’, 39: ‘과’, 40: ‘비둘기’, 41: ‘강아지’, 42: ‘토끼’, 43: ‘노새’, 44: ‘노루’, 45: ‘프란시스’, 46: ‘쟘’, 47: ‘라이너’, 48: ‘마리아’, 49: ‘릴케’, 50: ‘이런’, 51: ‘시인’, 52: ‘의’, 53: ‘이름’, 54: ‘을’, 55: ‘불러’, 56: ‘봅니다’
- [0,1]의 범위 안에서 나눠서 인코딩하는 경우
- 일정 범위 안에서 쪼갤 수 있지만 상대적 거리는 달라짐
- ex. '어머님-별', '소학교-을' 은 모두 사이에 2개의 형태소를 두고 있지만 거리는 0.273, 0.055로 상대적 거리는 다르다.
- 0: ‘어머님’, 0.091: ‘나’, 0.182: ‘는’, 0.273: ‘별’, 0.364: ‘하나’, 0.455: ‘에’, 0.545: ‘아름다운’, 0.636: ‘말’, 0.727: ‘한마디’, 0.818: ‘씩’, 0.909: ‘불러’, 1: ‘봅니다’
- 0: ‘소학교’, 0.018: ‘때’, 0.036: ‘책상’, 0.055: ‘을’, 0.073: ‘같이’, 0.091: ‘했’, 0.109: ‘던’, 0.127: ‘아이’, 0.145: ‘들’, 0.164: ‘의’, 0.182: ‘이름’, 0.2: ‘과’, 0.218: ‘패’, 0.236: ‘경’, 0.255: ‘옥’, 0.273: ‘이런’, 0.291: ‘이국’, 0.309: ‘소녀’, 0.327: ‘들’, 0.345: ‘의’, 0.364: ‘이름’, 0.382: ‘과’, 0.4: ‘벌써’, 0.418: ‘애기’, 0.436: ‘어머니’, 0.455: ‘된’, 0.473: ‘계집애’, 0.491: ‘들’, 0.509: ‘의’, 0.527: ‘이름’, 0.545: ‘과’, 0.564: ‘가난’, 0.582: ‘한’, 0.6: ‘이웃’, 0.618: ‘사람’, 0.636: ‘들’, 0.655: ‘의’, 0.673: ‘이름’, 0.691: ‘과’, 0.709: ‘비둘기’, 0.727: ‘강아지’, 0.745: ‘토끼’, 0.764: ‘노새’, 0.782: ‘노루’, 0.8: ‘프란시스’, 0.818: ‘쟘’, 0.836: ‘라이너’, 0.855: ‘마리아’, 0.873: ‘릴케’, 0.891: ‘이런’, 0.909: ‘시인’, 0.927: ‘의’, 0.945: ‘이름’, 0.964: ‘을’, 0.982: ‘불러’, 1: ‘봅니다’
- 따라서 일정 범위 안에서 쪼갤 수 있으면서 상대거리도 지키기 위해 사인/코사인 함수를 사용
5. 어텐션(Attention)
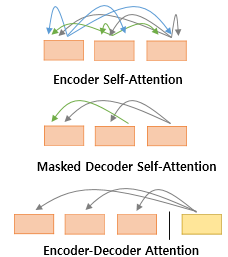
- 트랜스포머에 사용되는 세 가지의 어텐션
- Encoder Self-Attention (Query = Key = Value)
- Masked Decoder Self-Attention (Query = Key = Value)
- Encoder-Decoder Atttention : 디코더에서 (Query : 디코더 벡터 / Key = Value : 인코더 벡터)
- ※ 셀프 어텐션 : Query, Key, Value 벡터의 출처가 동일한 경우 (세번째 그림은 쿼리는 디코더에 키값이 인코더에 있으므로 셀프 어텐션이 아니다.)
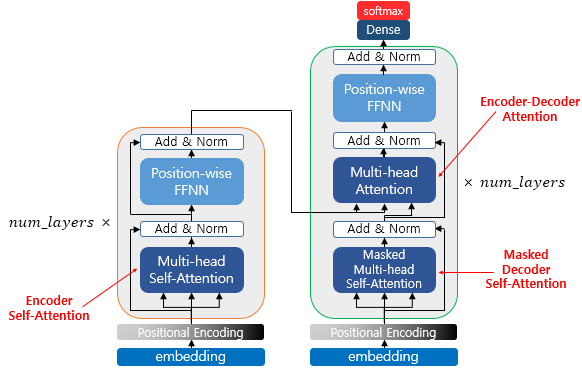
- 위의 세가지 어텐션이 이루지는 곳
- Multi-Head : 트랜스포머가 어텐션을 병렬적으로 수행하는 방법
6. 인코더(Encoder)
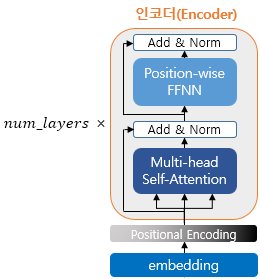
- 인코더 층을 num_layers 만큼 쌓는다.(논문 : 6)
- 하나의 인코더는 2개의 서브층(sublayer)으로 나뉜다.
- 셀프 어텐션
- 피드 포워드 신경망
- 하나의 인코더는 2개의 서브층(sublayer)으로 나뉜다.
7. 인코더의 셀프 어텐션
<첫 번째 서브층>
1) 셀프 어텐션의 의미와 이점
- 셀프 어텐션 : 자기 자신에게 어텐션을 수행
- 기존 어텐션은 디코더와 인코더(다른 문장)간의 유사성을 파악했다면 셀프 어텐션은 입력 문장의 단어들 간의 유사성을 파악
셀프어텐션
Q : 입력 문장의 모든 단어 벡터들
K : 입력 문장의 모든 단어 벡터들
V : 입력 문장의 모든 단어 벡터들

<The animal didn't cross the street because it was too tired.> = <그 동물은 길은 건너지 않았다. 왜냐하면 그것은 너무 피곤하였기 때문이다.>
- it 이 animal 이라는 것을 사람은 쉽게 알 수 있지만 기계는 알 수 없다. 셀프 어텐션은 입력 문장 내의 단어들끼리 유사도를 구ㅐ it이 animal과 연관될 확률이 높다는 것을 찾아낸다.
2) Q, K, V 벡터 얻기
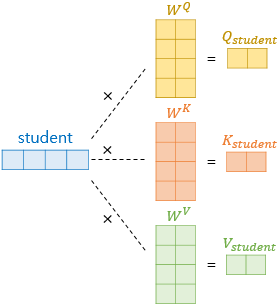
- 각 단어 벡터들로부터 Q, K, V 벡터를 얻는 작업
- dmodel = 512 를 가졌던 각 단어벡터들을 64벡터를 갖는 Q, K, V 벡터로 변환
- 64 라는 숫자의 결정 : num_heads를 8로 설정했기 때문에 512/8=64이 된다.
💡 num_heads : 병렬의 개수. 어텐션을 여러개로 분할하여 병렬로 수행하여 결과값을 다시 하나로 합침.
- 기존 벡터 × 가중치 행렬(dmodel/(dmodel/num_heads)) = Q, V, K
3) 스케일드 닷-프로덕트 어텐션(Scaled dot-product Attention)
- 여기서부터 기존의 어텐션과 같다
- 아래 과정은 모든 Q 벡터에 대해서 반복
- 1️⃣ 각 Q벡터는 모든 K벡터에 대해서 어텐션 스코어를 구함 2️⃣ 어텐션 분포 구함 3️⃣ 모든 V벡터를 가중합하여 어텐션값(컨덱스트 벡터) 구함
- 트랜스포머에서는 스케일드 닷 프로덕트 어텐션을 사용한다.
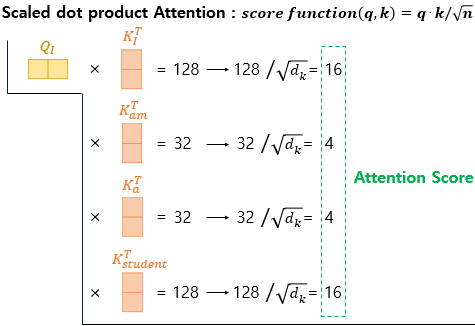
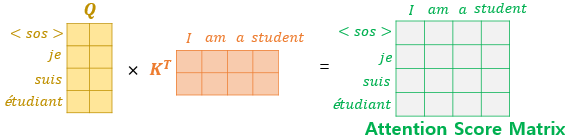
1️⃣ 단어 'I' 에 대한 Q 벡터가 모든 K 벡터에 대해서 어텐션 스코어를 구하는 과정.
- 이 과정을 'am', 'a', 'student'에 대한 Q벡터가 모든 K벡터에 대해서 동일하게 함
- 어텐션 스코어는 단어 I 가 I, am, a, student 와 얼마나 연관있는지 수치로 나타낸 것
- dk = dmodel/num_heads = 64 -> 루트 씌우면 8
- 소프트맥스 함수에서 값이 너무 커지면 발산하기 때문에 스케일링하여 역전파 시 기울기 소실 문제를 완화하기 위해 사용
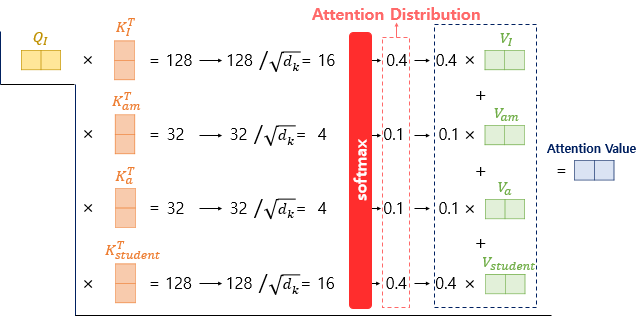
2️⃣ 어텐션분포를 구함(소프트맥스) 3️⃣ 각 V벡터와 가중합하여 어텐션 값(컨텍스트 벡터)을 구함
- 소프트맥스를 거친 값에 V를 곱해주면 Q와 유사한 V일수록 (중요한 V) 더 높은 값을 가짐 (어텐션의 원리)
- I, am, a, student 각각에 대한 어텐션 값 구함
-> I, am, a, student 에 대한 Q벡터를 일일히 연산해야할까? (X)
4) 행렬 연산으로 일괄 처리하기
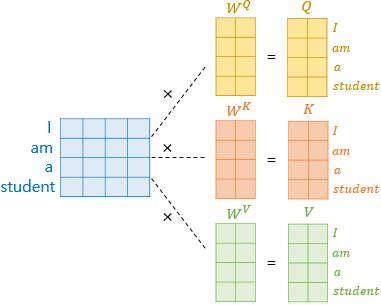
- 벡터 연산이 아닌 행렬 연산을 통해 일괄 연산 (실제로 벡터가 아닌 행렬로 연산된다)
1️⃣ Q, K, V 행렬 구하기- 단어 벡터마다 가중치 행렬을 곱하는게 아니라 문장 벡터에 가중치 행렬을 곱해 Q, K, V 행렬을 구한다.
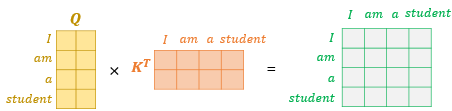
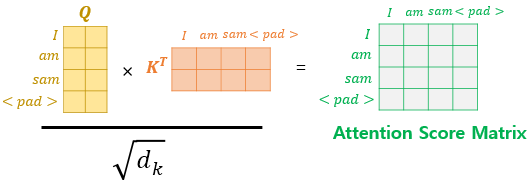
2️⃣ 어텐션 스코어 구하기
- Q행렬 × K 전치 행렬 을 하면 Q벡터와 K벡터의 내적이 원소가 됨.
- 이렇게 만들어진 행렬을 루트 dk 로 나눠주면 (스케일드 닷-프로덕트) 어텐션 스코어 행렬을 구할 수 있음

3️⃣ 어텐션 분포 / 어텐션 값 구함
입력 문장의 길이 : sep_len
문장 행렬의 크기 : (sep_len, dmodel)
Q 벡터, K 벡터 : dk -> Q 행렬, K 행렬 : (sep_len, dk)
V 벡터 : dv -> V 행렬 : (sep_len, dv)
가중치 행렬 WQ, WK : (dmodel, dk)
WV : (dmode, dv)
어텐션 값 행렬 : (seq_len, dv) (Q, K전치, V 곱함)
5) 스케일드 닷-프로덕트 어텐션 구현하기
6) 멀티 헤드 어텐션(Multi-head Attention)
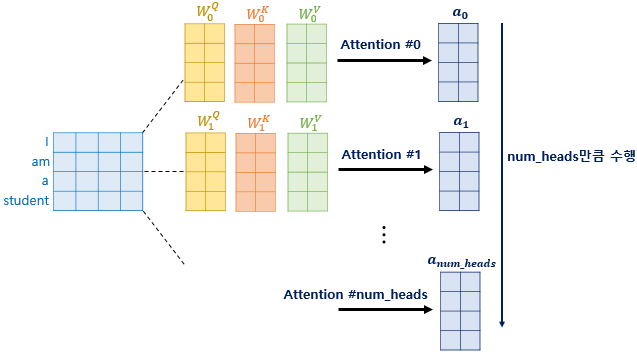
- Multi-Head : 트랜스포머가 어텐션을 병렬적으로 수행하는 방법
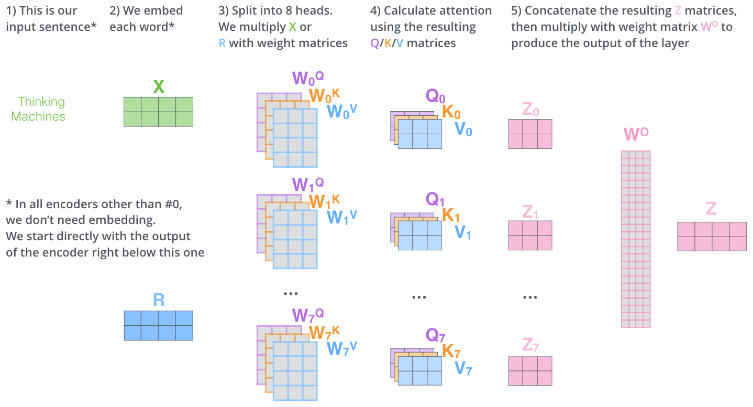
- 동일 Q, K, V에 각각 다른 가중치 행렬을 곱해줌
- 논문 기준 512의 단어 벡터를 8로 나누어 64차원의 Q, K, V벡터로 바꿈
- 어텐션 헤드 : 각각의 어텐션 값 행렬
- WQ, WK, WV는 각각의 어텐션 헤드마다 다르다
- 왜 한번의 어텐션보다 차원을 축소시켜 여러번의 어텐션을 병렬로 사용하는 것이 효과적인지
- 연산 속도를 높일 수 있다
- 여러 시각에서 정보를 수집
- ex. '그 동물은 길을 건너지 않았다. 왜냐하면 그것은 너무 피곤하였기 때문이다.'
- Q 가 그것(it)이라고 할 때 첫번째 어텐션 헤드는 it-animal의 연관도를 높게 본다면 두번째 어텐션 헤드는 it-tired의 연관도를 높게 볼 수 있다.
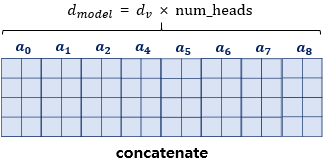
- 병렬 어텐션이 끝나면 모든 어텐션 헤드를 concat함
- 크기는 (seq_len, dmodel)
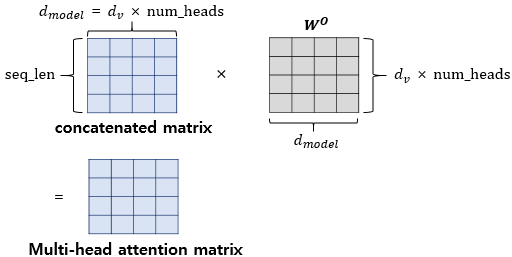
-
어텐션 헤드를 모두 연결한 행렬에 가중치 행렬 Wo를 곱해준다 : 최종 결과물
- 💡 인코더의 입력으로 들어왔던 행렬의 크기가 유지되고 있음
- 두 서브층(멀티 헤드 어텐션, 포지션 와이즈 피드 포워드 신경망)을 지나면서 행렬의 크기가 유지되어야함 : 인코더 층을 여러개 쌓았기 때문에 크기가 유지되어야 다음 인코더층의 입력이 될 수 있기 때문
- 💡 인코더의 입력으로 들어왔던 행렬의 크기가 유지되고 있음
-
가중치
- WQ, WK, WV : Q, V, K 벡터를 만드는 가중치
- Wo : 어텐션 헤드 concat 후 곱해주는 가중치
8) 패딩 마스크(Padding Mask)
- 입력 문장의 <PAD> 토큰을 어텐션 연산에서 제외하기 위해서
- 스케일드 닷 프로덕트 어텐션 함수 내부에서 mask라는 값을 인자로 받아서, 이 mask값에다가 -1e9라는 아주 작은 음수값을 곱한 후 어텐션 스코어 행렬에 더해주고 있음
-
패드가 포함된 입력 문장의 셀프 어텐션
-
실질적 의미가 없는 <PAD>를 유사도를 구하는 과정에서 제외하기 위해서 Masking해줌
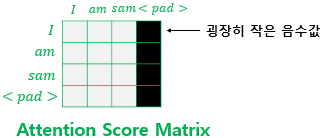
- Key(열)에 <PAD>가 있는 경우 해당 열 전체를 마스킹
- 매우 작은 음수값 : -1,000,000,000과 같은 -무한대에 가까운 수
- 이 값은 소프트맥스 함수를 거치면서 0에 굉장이 가까운 값이 된다 -> 유사도에 반영 X
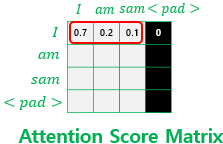
(소프트맥스 함수를 지난 후를 가정)
- 각 행의 총 합 (가중치의 합)은 1이 되는데 <PAD> 는 0이 되어 의미 없음
8. 포지션-와이즈 피드 포워드 신경망(Position-wise FFNN)
<두 번째 서브층>
- 포지션 와이즈 FFNN = 완전 연결(Fully-connected) FFNN
- 포지션 와이즈 : 개별 단어마다 적용
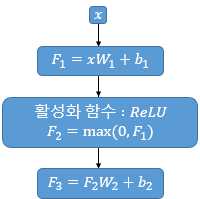
x : 멀티 헤드 에텐션의 결과 (seq_len, dmodel)
W1 : 가중치 행렬 (dmodel, dff) (dff는 2048로 설정)
- W1, b1, W2, b2 는 하나의 인코더 층 내에서 모든 문장, 단어마다 동일하게 사용 됨. (인코더층마다는 다름)
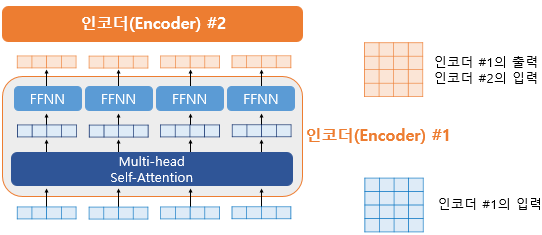
- 하나의 인코더층을 지난 행렬이 다음 인코더 층의 입력으로 전달 (이 과정이 반복)
- 최종 출력은 인코더의 입력 크기를 유지하고 있음
9. 잔차 연결(Residual connection)과 층 정규화(Layer Normalization)
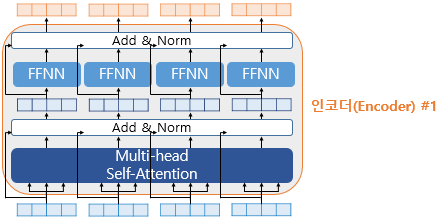
Add & Norm = 잔차 연결과 층 정규화
1) 잔차 연결(Residual connection)
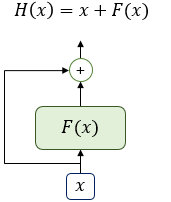
- F(x) : 서브층
- 잔차연결 : 서브층의 입력과 출력을 더하는 것 (둘이 같은 차원을 가지므로 덧셈 가능)
- 모델의 학습을 돕는 기법 : 하위층에서 학습된 정보가 손실되는 것을 방지
- x+Sublayer(x)
- 멀티 헤드 어텐션에서 잔차 연결 연산 : H(x) = x+Multi-head Attention(x)
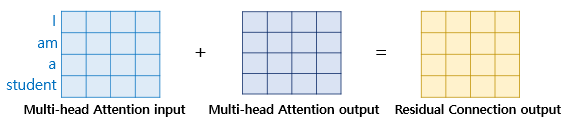
2) 층 정규화(Layer Normalization)
- LN = LayerNorm(x+Sublayer(x))
- 층 정규화 : 텐서의 마지막 차원(dmodel 차원)에 대해서 평균과 분산을 구하고 수식을 통해 정규화함
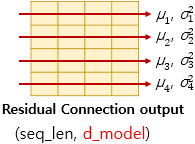
- 화살표 방향으로 각각 평균과 분산을 구함
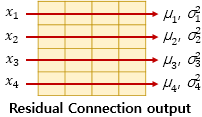
- LN = LayerNorm(x+Sublayer(x)) : 층 정규화 수행 후 벡터 xi는 lni라는 벡터로 정규화
1️⃣ 평균과 분산을 통한 정규화 : 평균과 분산을 통해 벡터 xi를 정규화
벡터 xi의 k차원의 값이 평균과 분산에 의해 정규화
2️⃣ 감마와 베타를 도입
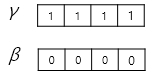
- 초기값 : 감마(1) 베타(0)
- 학습 가능한 파라미터
- 최종 수식
12. 인코더에서 디코더로(From Encoder To Decoder)
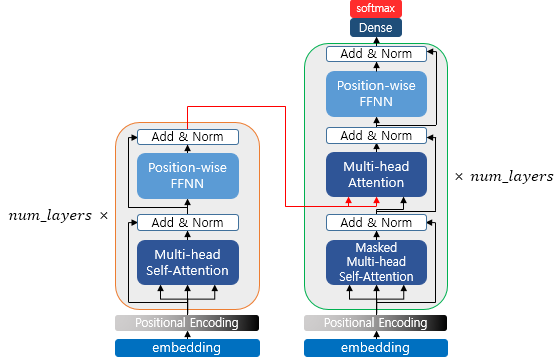
- num_layers 만큼 순차적 연산을 통해 마지막 층의 출력을 디코더로 전달
- 디코더로 num_layers만큼 연산을 한다. (인코더의 출력을 각 디코더의 층 연산에 사용)
13. 디코더의 첫번째 서브층 : 셀프 어텐션과 룩-어헤드 마스크
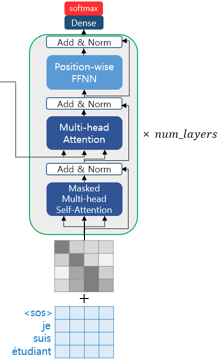
-
디코더도 인코더와 마찬가지
- 임베딩 층 -> 포지셔널 인코딩 -> 문장행렬 입력
- 교사강요를 사용하여 훈련되므로 번역할 문장에 해당되는 <sos> je suis étudiant의 문장 행렬을 한 번에 입력받음
-
문제 :
- seq2seq는 매 시점마다 순차적으로 입력 받아 다음 단어 예측에 이전 입력된 단어만 참고
- suis 예측 시 <sos>와 je 만 입력됨
- 트랜스포머는 문장 행렬 단위로 입력을 한번에 받아 미래 시점 단어도 참고하는 현상 발생
- suis 예측 시 이미 je suis étudiant 입력됨
- seq2seq는 매 시점마다 순차적으로 입력 받아 다음 단어 예측에 이전 입력된 단어만 참고
-
룩 어헤드 마스크를 도입
- 미래 시점의 단어들을 참고하지 못하도록 (해당 시점에서의 결과값 예측은 미리 알고 있는 output에만 의존)
- 미리보기에 대한 마스크
- 인코더와 달리 순차적으로 결과를 만들어내기 때문에 셀프 어텐션을 변형
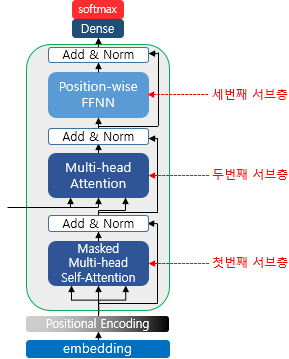
- 디코더의 첫번째 서브층 : 인코더의 첫번째 서브층인 멀티 헤드 어텐션 층과 동일 연산
- 어텐션 스코어 행렬에서 마스킹을 하는 차이점
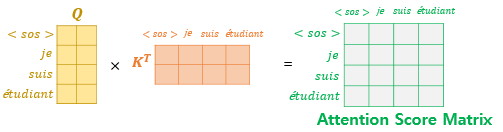
- 셀프 어텐션을 통해 어텐션 스코어 행렬 얻음
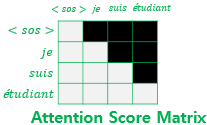
- 미래 시점의 단어들을 참고하지 못하도록 마스킹
- 마스킹 하고자 하는 위치에 1을 하지 않는 위치에 0을 리턴
14. 디코더의 두번째 서브층 : 인코더-디코더 어텐션
- 디코더의 두번째 서브층 : 멀티헤드연산. 셀프어텐션이 아니고 인코더-디코더 어텐션
- 인코더-디코더 어텐션: 쿼리가 디코더, 키값이 인코더 행렬
- 셀프어텐션 : Q=V=K
인코더의 첫번째 서브층 : Query = Key = Value
디코더의 첫번째 서브층 : Query = Key = Value
디코더의 두번째 서브층 : Query : 디코더 행렬 / Key = Value : 인코더 행렬
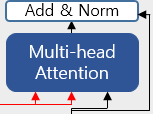
- K, V : 인코더의 마지막 층으로부터 두 개의 화살표
- Q : 디코더의 첫번째 서브층의 결과 행렬로부터