L1, L2 Regularization

스르륵·2021년 4월 7일

Regularization machine learning

부트캠프 정리하기

목록 보기

7/12

정규화에 대한 내용 정리

overfitting 방지를 위한 방법 중 하나
L1 norm, L2 norm의 컨셉을 가져와 학습에 영향을 미치는 cost function을 조정하는 것

L1 norm, L2 norm

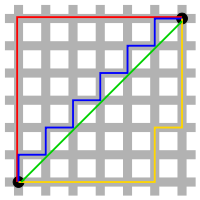
벡터 사이의 거리를 norm이라고 하고 두 벡터의 거리를 구하는 방법에는 2 가지가 있다. 이것이 바로 L1, L2 norm.

1) L1 norm

두 벡터 간의 거리를 절댓값으로 구하는 것.
위 그림에서 초록색을 제외한 나머지가 모두 L1 norm을 나타냄

\left\lVert x\right\rVert_1 = \sum_{i=1}^n |p_i - q_i|

두 벡터를 빼고 절댓값을 취한뒤 모두 더한 것.

2) L2 norm

유클리디안 거리이다.

\left\lVert x\right\rVert_2 = \sqrt {x_1^2+...+x_2^2}

오랫동안 두 점 사이의 거리로 사용했던 Euclidean Distance
위그림의 초록색 선이 L2 norm

이 둘을 응용한 L1 loss와 L2 loss는 딥러닝 파트에서도 나올 예정이니 알아두자
수식은 사실상 같고 L2에서만 제곱근을 취하지 않는다는 차이만 있음

정규화?

정규화란 회귀 계수가 가질 수 있는 값에 제약 조건을 부여하는 것이다. 데이터에 대한 모델의 오차 중 variance를 낮추어 일반화 성능을 높이는 것이다.

선형 회귀 모델에서 L1과 L2

L1 --> lasso regression
L2 --> Ridge regression

일단 적어두지만 아직 무슨소리인지 모르겠다.
딥러닝까지 시간있으니 공부하자

Regularization

1) L1 regularization

Cost = \sum_{i=0}^N(y_i - \sum_{j=0}^Mx_{ij}W_j)^2\ +\ \lambda\sum_{j=0}^M|W_j|

첫 번째 항은 원래의 cost function이고 여기에 가중치 절댓값을 더해준다.
~~편미분을 하면 $W$ 는 상수가 되고~~ (--> 이 부분은 공부 필요)
가중치가 너무 작은 경우 상수 값에 의해 wieght가 0이 되어 사라진다.

2) L2 regularization

Cost = \sum_{i=0}^N(y_i - \sum_{j=0}^Mx_{ij}W_j)^2\ +\ \lambda\sum_{j=0}^MW_j^2

역시 첫 번째 항인 cost function에 가중치를 제곱하여 더해줌으로서 편미분하여 backpropagation 할 때 cost뿐 아니라 가중치도 줄어드는 방식으로 학습한다.
특정 가중치가 비이성적으로 커지는 것을 막는다.
--> 전체적으로 가중치를 작아지게 하여 과적합을 방지한다.

참고한 글
L1, L2 Norm, Loss, Regularization?
Regularized Linear Regression
L1 Regularization의 Gradient에 관한 소고