머신러닝의 평가지표

머신러닝 모델을 평가하는 평가지표의 종류와 장단점 혹은 언제 쓰이는지 알아보자

• classification
  - precision
  - recall
  - f1-score
  - ROC, AOU
• regression
  - MSE, MAE

Bias, Variance Trade-off

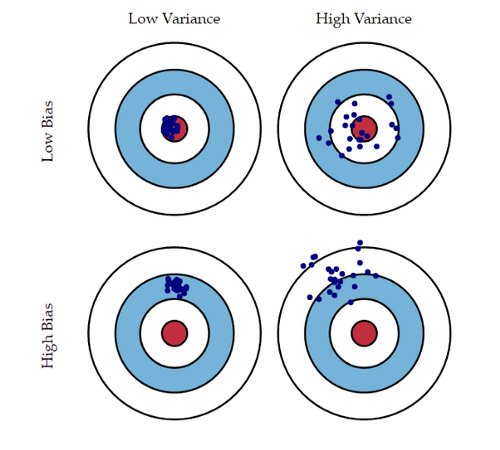
low bias - low variance가 가장 이상적인 모델이지만 현실적으로는 둘 사이를 타협하며 성능을 향상시켜 가야한다.

classification metrics

Accuracy가 가장 일반적으로 쓰이지만 단점이 있음! 예를들면, 실제 데이터 100개 중 80개가 False, 20개가 True일때, 모델의 예측결과가 전부 False로 예측해도 accuracy는 80%가 된다. 하지만 task에 따라 이러한 평가지표가 올바른 결론을 도출하지 못할 수 있음

ex) 암 환자 판별하는 경우...
환자 수 보다 건강한 사람이 훨씬 많을 것. 그렇다면 실제 환자 수 중 환자로 판별된 수를 보는 것이 더 정확한 성능 지표가 될 것 (Recall)

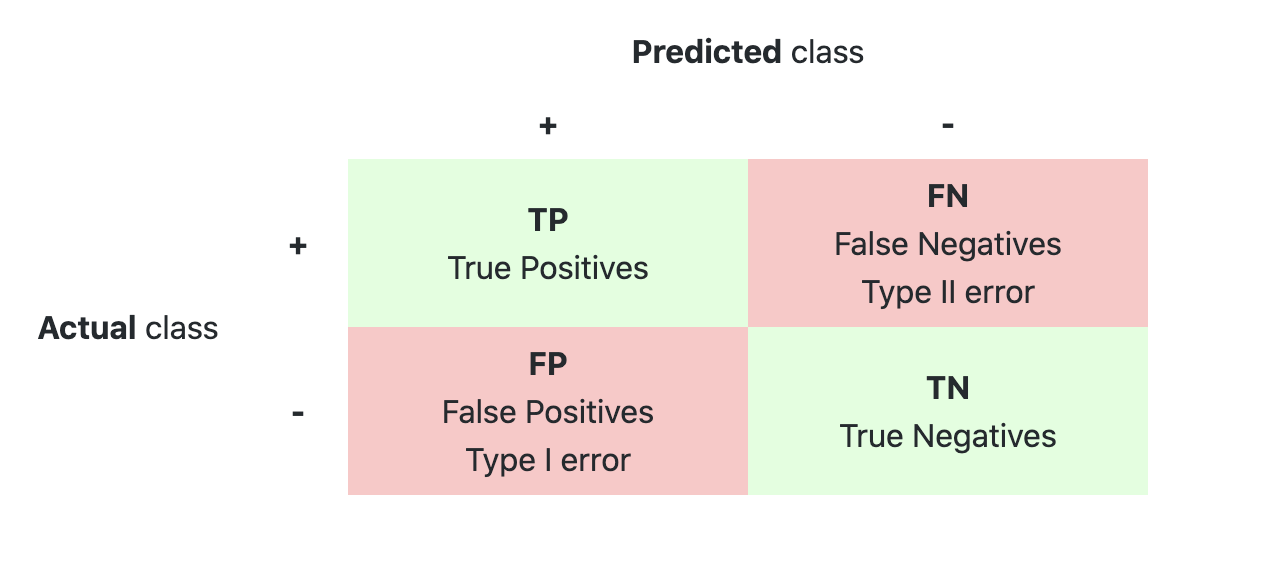
1) Precision

모델이 positive로 분류한 것들 중 실제 positive인 비율

2) recall

실제로 positive인 것들 중 positive로 분류된 것의 비율

3) F1-score

precision과 recall의 조화평균을 통해 극단적 이상치에 대응한다.

precision-recall trade off

precision과 recall은 위에서 본 bias, variance trade-off와 같은 관계를 가지고 있다. 둘 중 하나를 극단적으로 높이면 나머지는 낮아질 수 밖에 없다. 이때 분류 결정 threshold를 통해 둘을 조절하게 된다.

• threshold 상승 --> positive로 판단이 더 빡빡해짐 --> FP낮아짐 --> precition 상승
• threshold 하강 --> positive로 판단이 느슨해짐 --> FP늘어남 --> precision 하락

recall에서도 비슷한 결과가 나온다.

• threshold 상승 --> FN 증가 --> recall 하락
• threshold 하락 --> FN 감소 --> recall 상승

Regression Metric

1) MSE

• Mean Squared Error
• $\frac{1}{N}\sum_{i=1}^{N}(y_{i}-\hat{y_{i}})^{2}$
• 극단적 oulier에 취약할 것
• 예측값의 평균 squared error를 계산

2) MAE

• Mean Absolute error
• $\frac{1}{N}\sum_{i=1}^{N}|y_{i}-\hat{y_{i}}|$
• finance에서 널리 사용된다고 한다
• robust to outlier