Heap-Sort
space = O(n)
insert & removeMin = O(log n)
size, empty, min = O(1)
n개의 요소의 sequence를 정렬하는 과정 -> O(n*log n)
-
1단계 : s가 빌 때까지 p에 삽입
한번 삽입하는데에 O(log n) 시간이 걸리므로, n 번 삽입하는데에는 총 O(n log n) 시간이 걸린다. -
2단계 : p가 빌 때까지 s에 삽입, p 하나씩 삭제
탐색 min은 O(1) 시간, 삭제 removeMin은 O(log n) 시간이 걸리므로 총 O(n log n) 시간이 걸린다.- heap을 이용한 sort 즉 Heap-sort는 총 O(n log n) 시간이 걸린다.
배열 기반 힙
우리는 길이가 n+1인 배열로 힙을 수행할 수 있다.
장점 - 인덱스로 접근이 바로 가능하다.
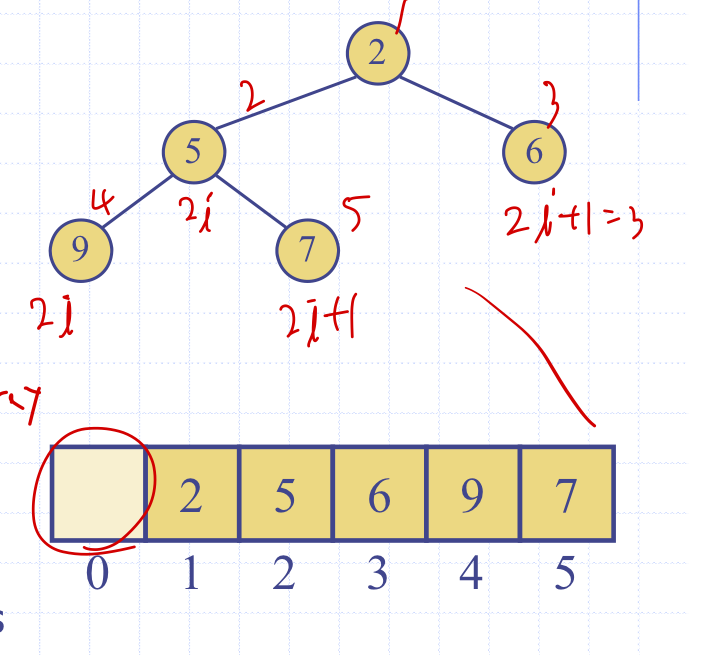
- rank i는 위 그림의 규칙과 같이 붙힌다.
- 0번째 셀은 사용하지 않는다.
- im-place 힙정렬을 이용한다.
In-Place Heap Sort
우리는 reverse comparator(비교연산자)를 사용한다.
- 가장 큰 요소가 탑에 있다고 가정 => max heap
- key(v) <= key(parent(v)) - 0번 랭크의 셀은 사용하지 않음.
첫단계: insertion업힙 사용
두번째 단계: removeMax
삽입과 삭제의 예시를 그림으로 보는 것이 이해가 빠르다.
삽입
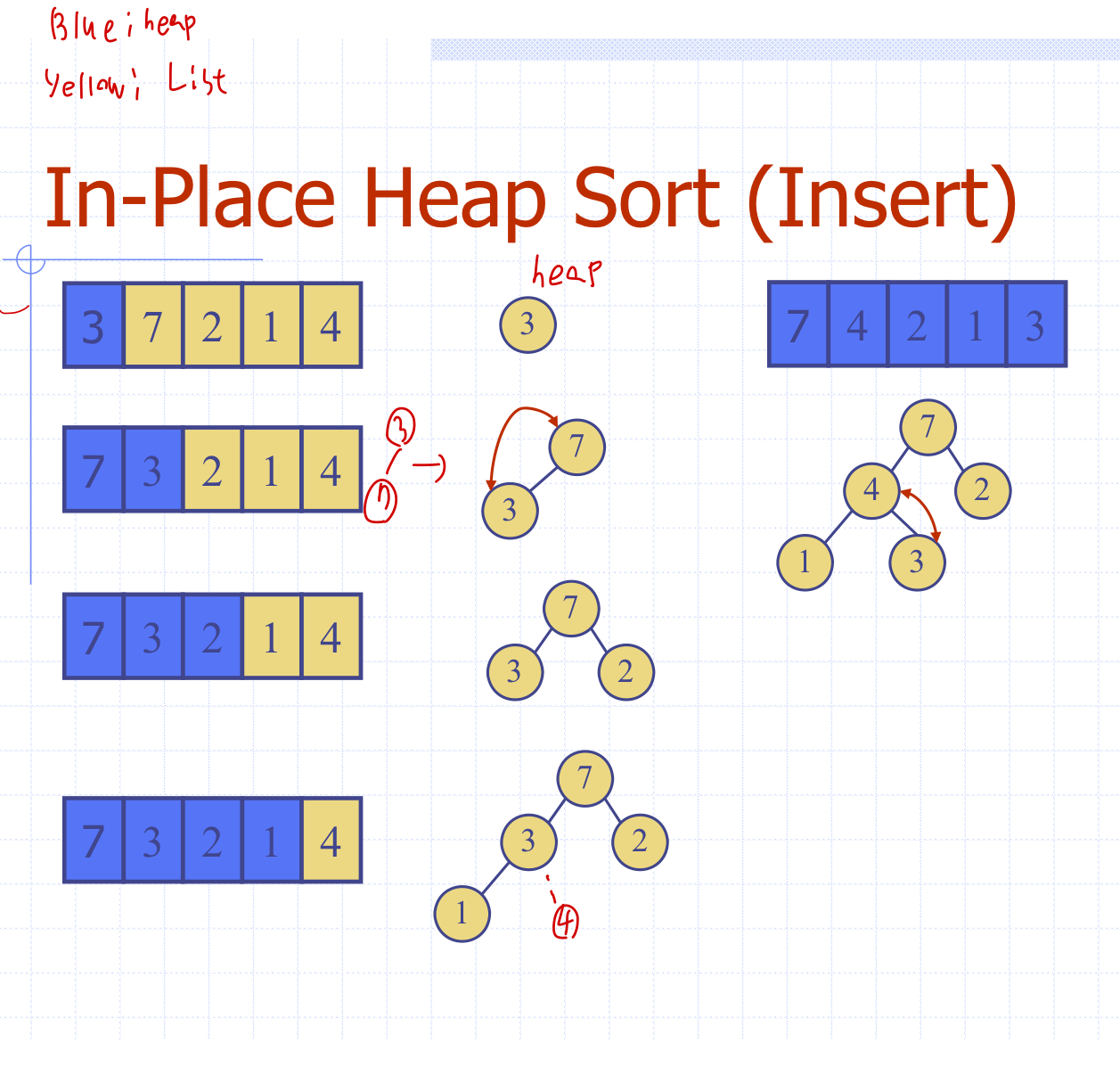
위 그림처럼 한 리스트에서 힙과 리스트가 공존한다.
삽입을 할 때마다 순서에 맞게 정렬해준다.
삭제
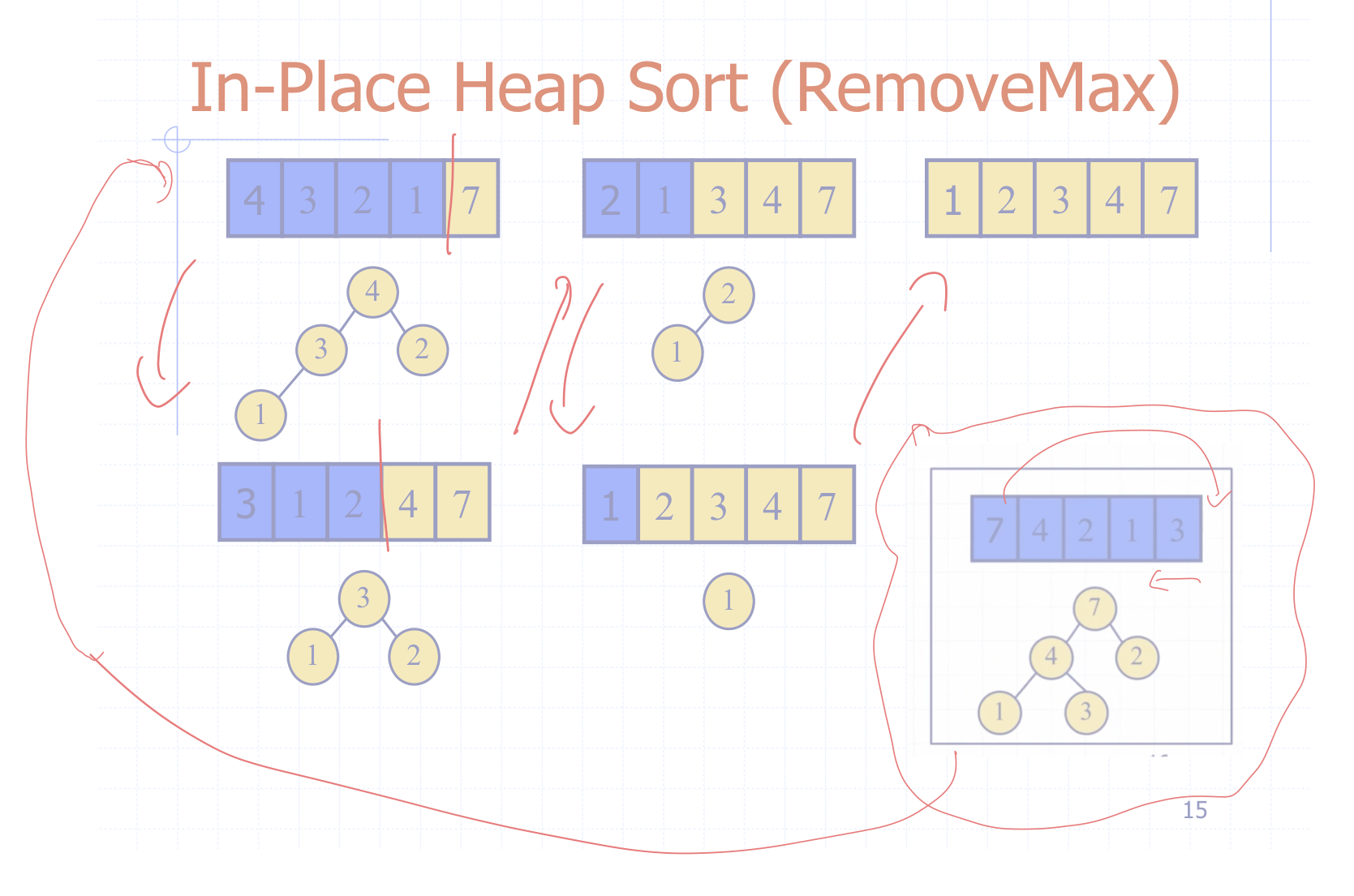
이번엔 삭제하는 과정이다.
최댓값이 리스트로 빠져나가며 힙에서 제거된다.
Merging
우리에게 두 개의 정렬된 힙과, key k가 주어지고, 이들을 합친다고 생각해보자.
1. 주어진 키 k를 루트노드로 삼고, 주어진 두 힙을 서브트리로 가져다붙힌다.
2. 다운힙을 통해 Heap-order property를 만족한다.
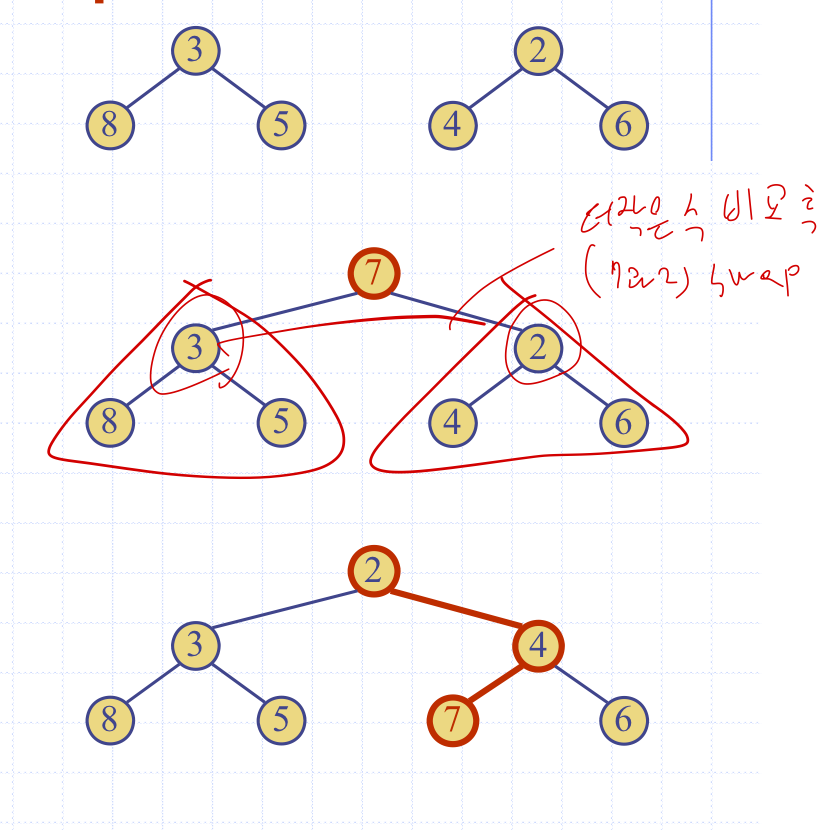
결과적으로 그냥 합치고 정렬했다면 O(nlog n)이었을 시간복잡도가 O(log n)이 된다.
Bottom-up Heap construction
Merging을 통해 효율적인 정렬 알고리즘을 완성할 수 있다.
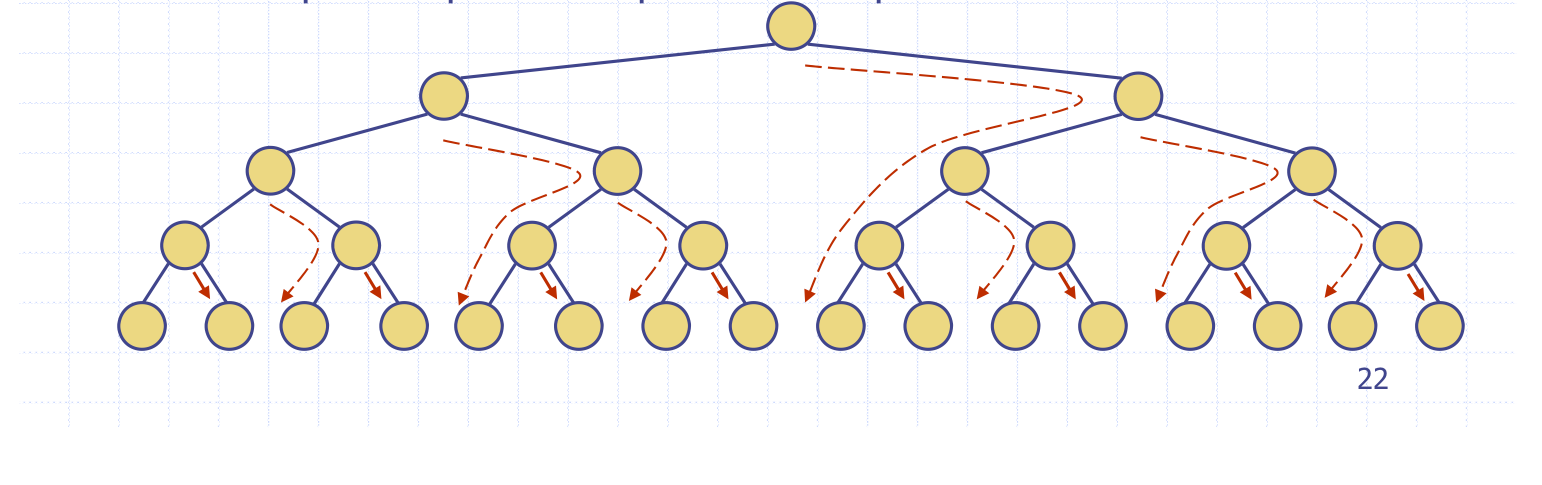
시간복잡도를 구해보자.
모든 노드가 처음엔 오른쪽으로 가고 그 후로 왼쪽으로 간다고 가정해보자.
O(n)
분석부분 이후에 수정.
