
Linear Regression -> Logistic Regression -> Binary Classification -> multi class classification
Linear Regression(선형회귀)라는 것은 Binary Classification(이진분류)에 적용하기에 단점이 존재하여 Logistic 이라는 것이 도입되었고, 결국 이 Logistic Regression은 Binary Classficication을 가능하게 하였습니다. 이진 분류는 더불어 Multi class classification도 할 수 있다는 것 까지 복습과 함께 배워보았습니다.
이렇게 새로운 방법론이 나온 이유와 또 그 방법론의 단점에의해 또 다른 방법론이 도출됐다라는 이러한 스토리라인업을 이해하고 있으면 좀 더 인공지능을 이해하고 기억하는데에 도움이 될 것 같아 정리하였습니다.
Review
-Linear Regression-
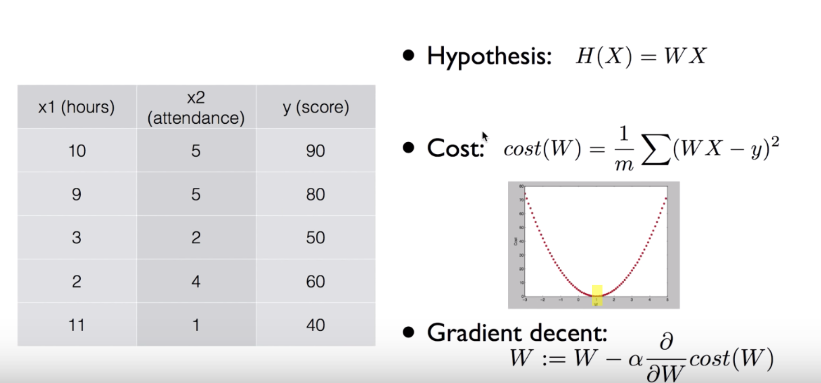
이러한 데이터에 의해서 10시간 공부하고 3번 출석 했을 시에 y(성적)은 몇인지 숫자를 예측하는 모델이 선형회귀 모델이었습니다.
이런 문제를 풀 때 Hypothesis(가설설정)를 H(X) = WX 라고 설정을 해주었습니다.
그 다음 Cost라는 함수를 정의 해주었습니다. 말 그대로 비용 함수 인데요, 즉 비용은 적게 들어가는 것이 좋으므로 Cost값이 적을 수록 좋습니다. 각각의 데이터들로 부터 가설설정으로 잡은 WX의 그래프와의 오차(거리 및 에러)값을 모두 더하여 평균을 내는 것이 Cost였습니다. 그래서 값이 작아진다는 것은 설정한 가설과 실제 데이터 값들의 '오차'가 줄어든다는 의미입니다.
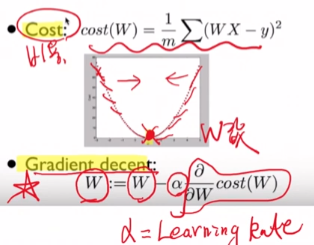
학습이라는 과정을 통해서 비용(cost)이 가장 적게 드는 W값을 찾는 과정이 학습의 과정이었고, 그 과정의 수학적 Solution은 Gradient Decent라는 경사 하강 방법론을 사용하였습니다.
-Binary Classification-
고양이 or 강아지, 합법 or 불법과 같은 그룹화 할 수 있는 것들을 '클래스'라고 정의 했었습니다. 또한 이러한 숫자로 표현이 된 것이 아닌 고양이냐 아니냐 같은 비정형 타입으로 정의 된 것들을 모두 범주형 라벨(데이터) 라고 합니다. 이러한 범주형 데이터들의 공통점은 수학적으로 공식화 가능하도록 Encoding이 되어야 합니다.
예를 들면 고양이 or 강아지를 0 or 1 같은 숫자로 라벨링 해주어야 하는 것입니다.
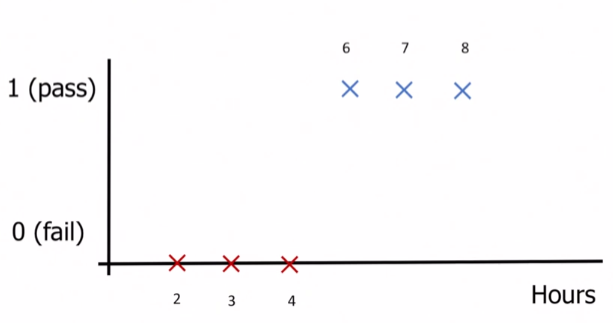
이 사진과 같이 2,3,4시간을 공부하면 시험에 불합격(0) 하고, 6,7,8시간을 공부하면 합격(1)이라고 하는 데이터가 있습니다.
이와 같은 데이터를 기반으로 10시간 공부한 사람은 합격을 할지 예측을 하고싶습니다.
이것을 Linear Regression을 활용해보겠습니다.
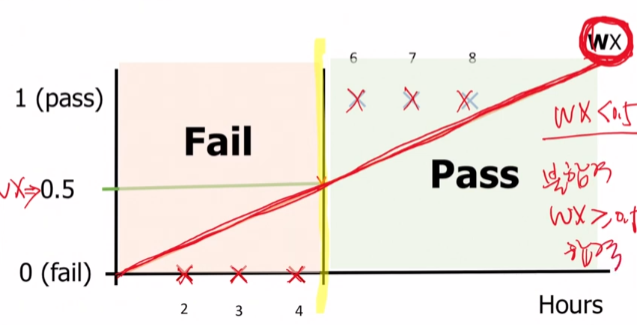
가설로 설정한 WX그래프를 기준으로 WX가 0.5보다 작으면 불합격, 크면 합격으로 예측을하면 정확하게 예측을 했을 것입니다.
1. 가설 설정 문제
하지만 여기엔 크나큰 단점이 있었습니다.
원래 데이터에 50시간 100시간 공부한 사람도 합격한 데이터가 있었다면 가설설정한 H(x)는 다음 사진과 같습니다.

이렇게 되면 설정한 가설 그래프가 살 짝 더 기울어져서 y값 0.5를 기준으로 더 작을 때 불합격이게 된다면 6시간 공부한 사람을 불합격으로 잘못 예측할 수 있습니다.
이렇게 많은 데이터가 있다면 Linear Regression으로는 Binary Classification을 제대로 예측하기 어렵습니다. 그래서 학자들은 고민하기 시작했습니다.

우리가 예측하기 위해 설정한 가설 H(x)는 1보다 크고 0보다 작을 수도 있습니다.하지만 정작 구해야하는 예측값들은 0또는 1로 딱 떨어집니다. 그래서 학자들은 0이상이며 1이하인 가설 H(x)를 재 설정하였습니다.
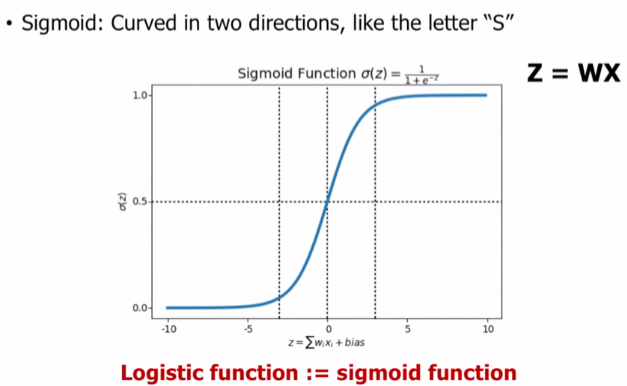
수학자들이 만들어 놓은 Sigmoid함수로 가설 설정을 하면 0과 1사이의 값을 도출해낼 수 있다라는 결론이 나옵니다. 이 함수는 모든 수를 0과 1사이로 Bound 시킬 수 있습니다.
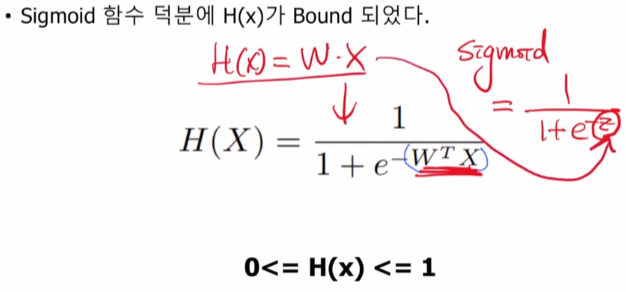
그래서 기존에 사용하였던 H(x)=W*X를 Sigmoid함수에 해당하는 z에 담아서 계산을 하게되면 0과 1사이로 Bound되어 결과를 도출해낼 수 있었습니다.
2. Local Minimum 문제, Cost 재설정
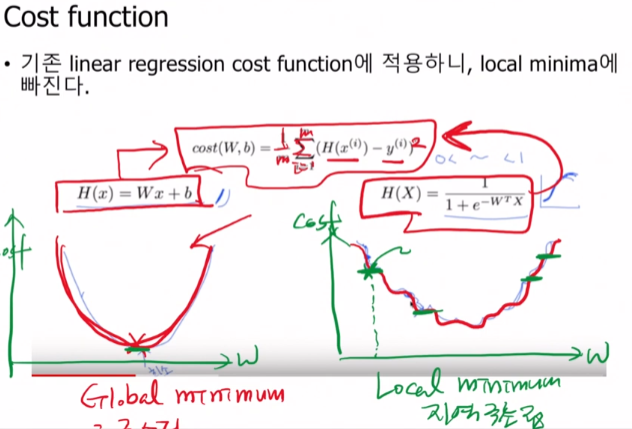
하지만 이렇게해도 Cost함수에서 여전히 문제가 있었습니다.
기존에 사용하였던 가설대로면 W가 최소가 되는, 0이 되는 지점인 Global Minimum을 알아낼 수 있었습니다.
하지만 Sigmoid를 사용하면서 그래프가 비규칙적으로 바뀌어 중간중간에 cost값이 0이 되는지점이 많이 존재하게 됩니다. 이 때를 Local Minimum(지역극소점)에 빠졌다고 표현하여 제대로 된 극소점을 찾지 못하게 되는 것 입니다.
그래서 Cost함수도 재 설계를 하여야합니다. 즉, 이진 분류를 하기위해 Cost는 정답에 가까워질수록 작아져야하고, 정답에 멀어질수록 커지게끔 설계를 해야합니다.
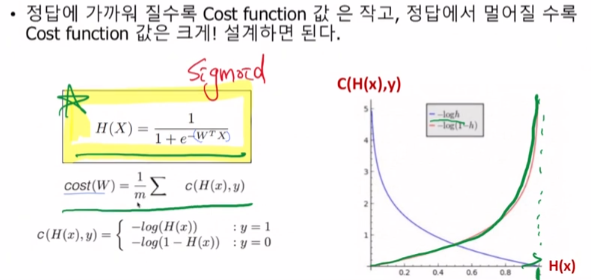
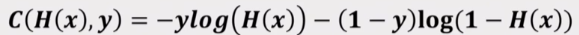
이렇듯 Logistic Function을 사용하여 cost값을 설계해주면 최소가 되는 W값을 찾을 수 있으며 이진분류를 제대로 예측하게 됩니다.
- 정리 -
이렇게 Linear Regression 에서 사용하였던 가설 설정으로는 Binary Classification에 사용하기엔 0보다 작고 1보다 큰 값이 나올 수도 있으며 제대로 된 값을 예측하기엔 역부족인 단점들이 존재하였습니다.
이를 해결하기 위해서 Sigmoid함수를 사용하여 0와1사이로 Bound시켜 주었지만 Local Minimum에 빠지는 현상을 또 해결하기 위해 Cost함수도 Logistic Function을 사용해 재설계를 해주어 결국 Binary Classification을 가능하게 만들었다는 일련의 스토리라인을 이해하게 되었습니다.
