어떤 문제가 주어졌을 때, 이 문제를 해결하는 방법을 알고리즘(algorithm)이라 한다.
알고리즘을 평가하는 대표적인 두 가지 기준은 시간복잡도와 공간복잡도이다.
알고리즘의 수행 시간은 대개 반복문이 수행되는 횟수로 측정한다.
반복문의 수행 횟수는 입력의 크기에 대한 함수로 표현된다.
지난 스터디에서 알고리즘 복잡도(complexity)와 실행 시간을 비교하며 몇 가지 알고리즘을 살펴 보았다. 대표적으로
- 이진 탐색(binary search) : 데이터의 양이 증가함에 따라 일의 양이 천천히 늘어나 효율이 높음 (logN)
- 선형 탐색(linear search) : 일의 양이 데이터의 양에 정비례함 (N)
- 선택 정렬(selection sort) : 데이터를 하나씩 비교하기 때문에 오래 걸림 (N²)
- 퀵 정렬(quick sort) : N(선형 탐색)보다는 효율이 낮지만 로그 인자가 상당히 느리게 증가해 N이 커질수록 효율이 높음 (NlogN)
이 밖에도 다른 복잡도를 갖는 알고리즘이 있다.
오늘은 지수 시간(Exponential-Time) 알고리즘과 다항 시간(Polynomial-Time) 알고리즘에 대해 알아보자.
지수 시간(Exponential-Time) 알고리즘
반복문의 수행 횟수가 2^N의 지수식으로 표현되면 지수 시간 알고리즘이다.
지수 시간은 가장 큰 수행 시간 중 하나이다.
지수 시간 알고리즘은 2^N의 비율로 증가하며, 지수 시간 알고리즘에서는 일의 양이 유난히 빠르게 늘어난다. 한 개의 항목이 추가되면 수행해야 할 일의 양이 2배가 된다. logN(이진 탐색)에서는 항목의 수를 2배로 늘려도 일의 단계는 1개만 늘어나므로 어떤 의미에서 지수 시간 알고리즘은 logN(이진 탐색) 알고리즘과 정반대라고 볼 수 있다.
지수 시간 알고리즘은 모든 가능한 경우를 하나씩 시도해 봐야만 하는 상황에서 사용된다.
그 대표적인 예로는
암호 기법
지수 시간 복잡도를 갖도록 하는 데 기반을 두는데 누군가 암호를 해독하기 위해서는 일일이 모든 경우의 수를 따져봐야 하기 때문에 큰N(긴 암호)을 갖는다면 암호를 해독할 확률이 사실상 희박하다. 그러므로 적의 공격을 방지할 수 있다.
다항 시간(Polynomial-Time) 알고리즘
반복문의 수행 횟수가 입력 크기의 다항식으로 표현되면 다항 시간 알고리즘이라 한다. 다항 알고리즘은 두 가지 알고리즘으로 나뉜다.
결정적 알고리즘(Deterministic Algorithm), 비결정적 알고리즘(Nondeterministic Algorithm).
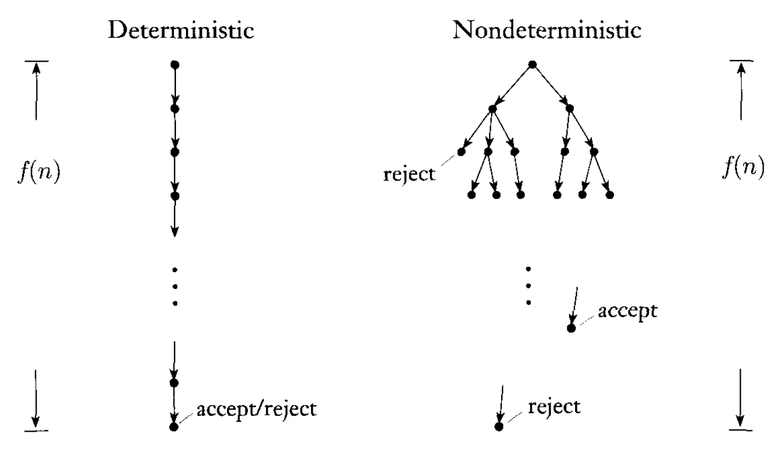
결정적 알고리즘(Deterministic Algorithm)
특정한 값을 입력하면 그에 따라 정해진 값이 나오는 것을 결정적 알고리즘이라고 한다. 수학공식이 가장 대표적인 예이다.
f(x) = x+1이라고 한다면 f(1) = 2, f(2) =3, f(k) = k+1으로 정해진대로 결과값이 나오게 된다.
비결정적 알고리즘(Nondeterministic Algorithm)
동일한 값을 입력해도 다른 결과를 출력할 수 있다고 정의할 수 있다.
[그림1] 결정적 알고리즘과 비결정적 알고리즘 비교 ▼
P vs NP
이론적으로는, 복잡도 종류와 관련된 용어이다.
복잡도 종류란, 계산 복잡도 이론에서 계산 복잡도에 따라 문제를 분류한 것이다.
- 복잡도 종류의 정의
추상기계 M이 O(f(n)) 만큼의 자원 R을 이용하여 풀 수 있는 문제의 종류 (n은 입력의 길이)
쉽게 말하자면, 문제가 쉬운가 어려운가에 따라 구분한 것이다.
문제가 쉽다는 것은 짧은 시간 내에 문제를 풀 수 있다는 것이고, 그렇지 않은 문제는 어려운 문제라는 것이다.
'P(Polynomial-time)' 문제
다항 시간(Polynomial-Time) 알고리즘으로 풀리는 결정적 문제(Decision Problem)의 집합.
결정적 문제는 Yes/No로 대답할 수 있는 문제이고, 답을 찾는 데 걸리는 시간이 짧은 문제다. 즉, 쉬운 문제이다.
'결정적'이라는 것은 계산 단계에서 하나의 가능성만을 고려하면 되는 것이다.
그러므로 하나의 input에서는 하나의 output만 나올 수 있다.
'NP(Non-deterministic Polynomial-time)' 문제
비결정적 다항 시간(polynomial-time nondeterministic) 알고리즘으로 풀리는 결정 문제(decision problem)의 집합.
비결정적 알고리즘은 결정적 알고리즘과는 다르게 매 단계 여러가지 가능성이 존재한다. 그러므로 하나의 input에 대해서 다른 output이 나올 수가 있다.
아주 간단하게 NP를 설명하자면, 풀기는 어려울 수 있지만, 답이 맞는지 확인하기는 쉬운 문제라는 의미로 받아들이면 된다.
[그림1] 참고
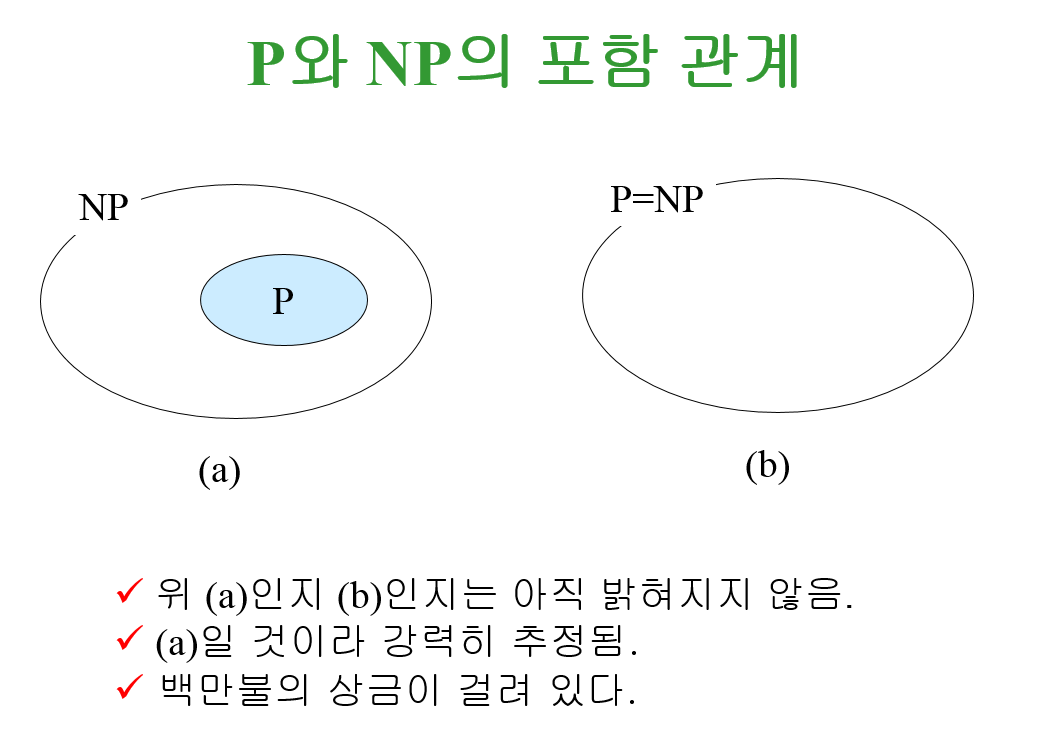
P와 NP의 관계
P문제가 주어졌을 때, 그 문제의 답이 YES라면, 그 답을 힌트삼아 그 문제의 답이 YES라는 것을 쉽게 확인할 수 있다. 그러므로 P문제는 NP이기도 하다. 즉, P는 NP에 속한다고 볼 수 있다.
그렇다면 P는 NP일까(P=NP)? 이는 아직 증명되지 않은 7개의 ‘밀레니엄 문제’ 중 하나이다. P=NP가 의미하는 바는 상당히 크다. 어떤 문제가 주어졌을 때 문제의 답을 쉽게 검산할 수 있다면 그 문제를 푸는 것도 쉽다는 말이 되기 때문이다.
[그림2] P와 NP의 포함 관계 ▼
[그림2]와 같은 문제가 중요하긴 하지만 현실적인 사안이라기보다는 이론적인 주제에 불과하다.
2000년, 클레이 수학 연구소(Clay Mathematics Institue)는 일곱 가지 미해결 문제에 대해 문제당 100만 달러의 상금을 걸었다.
10개 도시를 최단거리로 여행하는 법 (여행하는 외판원 문제)
NP문제 중 대표적인 예이다.
외판원은 자신이 사는 도시에서 출발해 어떤 순서로든 다른 도시를 모두 방문하고 나서 다시 출발점으로 돌아와야 한다. 여기서 목표는 각 도시를 정확히 한 번씩(반복 없이) 방문하고, 전체 여행한 거리를 최소로 만드는 것이다.
[그림3] 최근접 이웃 해법으로 풀이한 문제 ▼
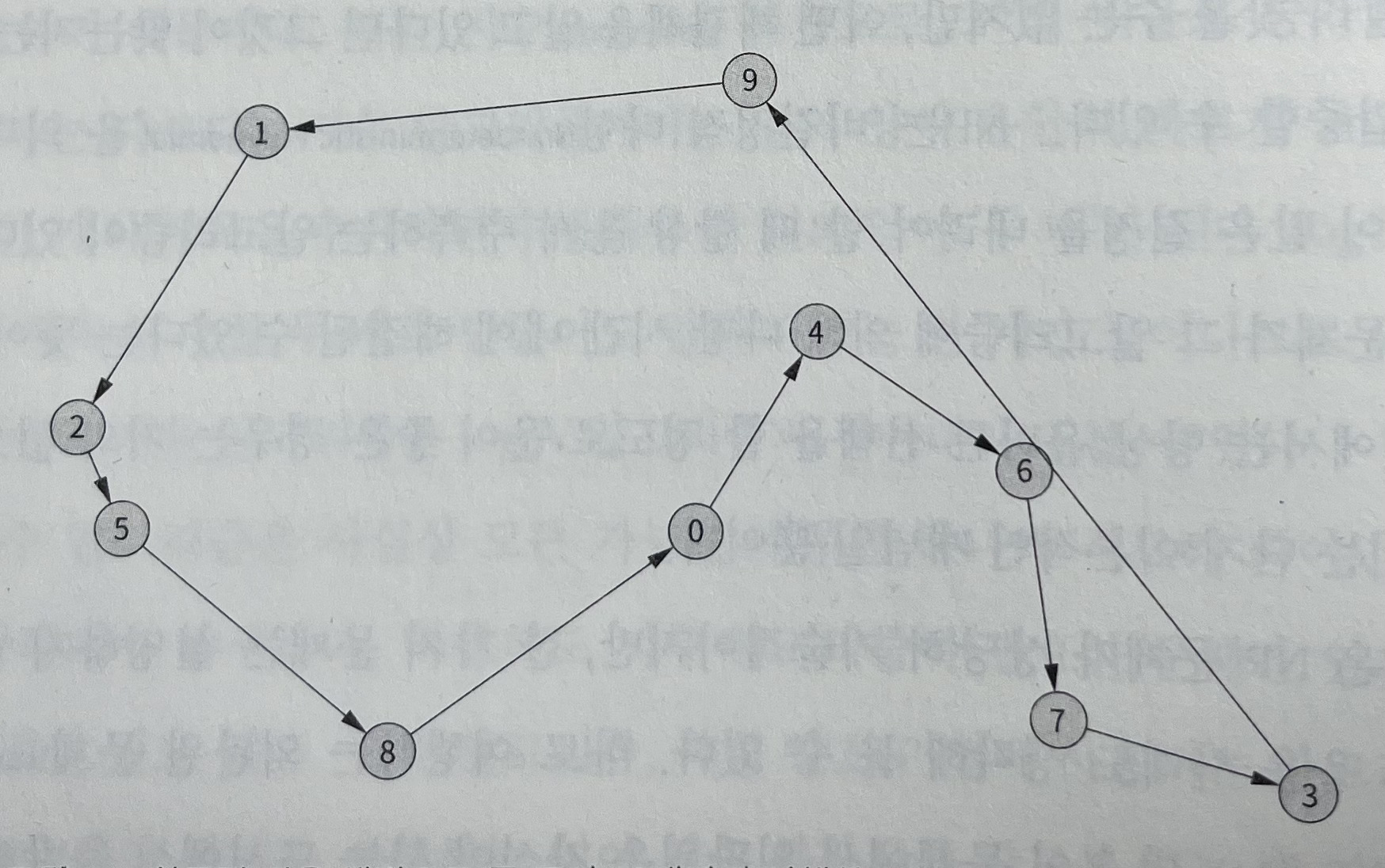
첫번째 풀이는 직관적으로 와 닿는 '최근접 이웃' 휴리스틱으로 찾은 해법이다. 한 도시에서 시작해 아직 방문하지 않은 도시 중 가장 가까운 도시로 이동하는 방식이다. (여행의 총 거리 12.92)
시작하는 도시가 바뀌면 여행 경로가 바뀔 수도 있다는 점 주의
[그림4] 최상의 해법으로 풀이한 문제 ▼
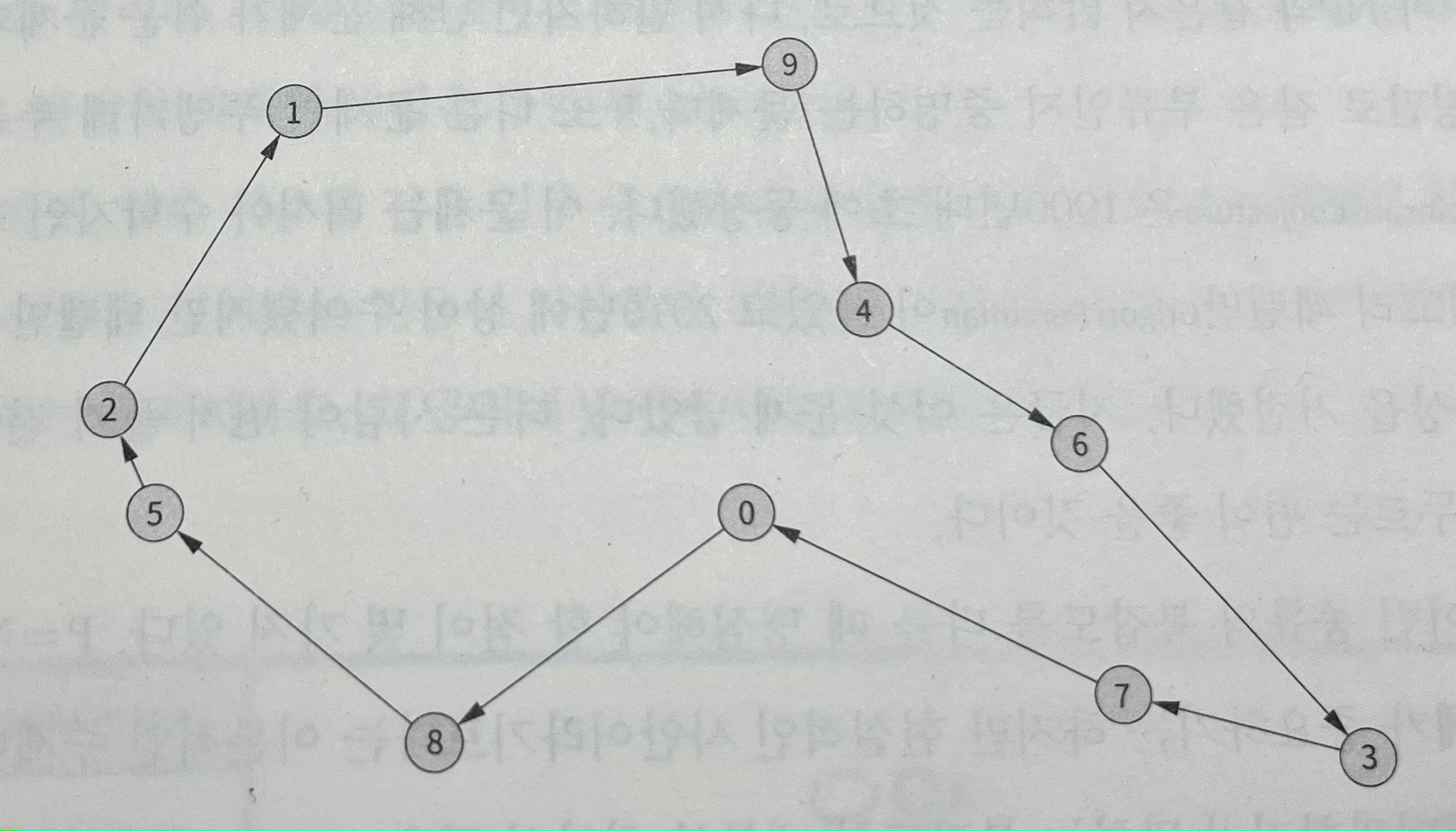
두번째 풀이는 모든 가능한 경로를 시도한 방법이다. 약 18만 개 경로 전체를 완전 탐색해서 찾아낸 최단 경로이다. (여행의 총 거리 11.86) 최근접 이웃 경로의 최단 거리보다 약 8% 짧다.
결론
가능한 모든 해법을 완전 탐색하는 것보다 더 효율적으로 풀 방법은 없다.
컴퓨터 과학자들이 말하는 복잡도란 대부분 최악의 경우(worst case)에 대한 것이지만 보통은 최악의 경우까지 가지 않는다. 어떤 문제(예를 들면 암호문제)는 답을 계산하는 데 극한의 시간이 필요하겠지만 모든 문제를 그렇게 난해하게 접근할 필요는 없다.
실제 상황에서는 대부분 근사치만 구하는 것으로도 충분할 수 있다. 완전히 최적인 해법을 구할 필요는 없다.
