FFT

들어가며

올 가을, 소음을 주제로 프로젝트를 진행했다. 도시의 소음을 측정하고 이를 AI가 분류한 데이터와 분석해 잠재적인 위험 요소를 선제적으로 파악하는 것이 목표였다.

소음을 측정하는 방법에 대해 조사하면서 "소음도", "배경소음도", "등가소음도", "A-가중 등가소음도"등 소음을 측정하는 상황과 목적마다 적합한 소음도가 있으며 소음을 규제하는 법에서는 소음 측정에 사용되는 환경과 방법에 대해서 전문적으로 설명하고 있다는 사실에 대해 알게 되었다. 흥미로운 것은 공사 현장에서 적용되는 "A-가중 등가소음도"으로, 이에 대해 공부하다가 퓨리에변환이라는 개념으로 이어지게 되어 개념을 정리해보고자 한다.

퓨리에 변환

퓨리에 변환은 시간이나 공간에서 샘플링된 신호를 시간 주파수 또는 공간 주파수에서 샘플링된 동일한 신호로 변환하는 수학적 공식이다. 즉 시간에 따른 진폭 변화를 갖는 주기 데이터에 대해서 어떤 주파수를 갖는 소리의 합성인지 분리해낼 수 있는 수학적 공식입니다.

일반적으로 주기적 데이터는 일정한 간격으로 반복되는 데이터로, 종종 사인 또는 코사인 파영으로 표시됩니다. 소리는 이러한 주기적인 데이터의 대표적인 예이다.

샘플 데이터 생성하기

파이썬에서 퓨리에변환을 이해하기 위해 Numpy 와 Matplotlib을 사용하여 데이터를 만들어보자 FFT(고속 퓨리에 변환)를 사용하면 손쉽게 퓨리에변환을 할 수 있다.

Fs = 1024 # Sampling Frequency, 1초에 측정되는 데이터의 개수
T = 1 / Fs # 데이터를 측정하는 주기

start_time = 0
end_time = 1 #

time = np.linspace(start_time, end_time, Fs) # 0초부터 1초까지 데이터를 Fs개수 만큼 나누어서 list 만들기 -> X축에 사용

# 4개의 주기 데이터를 생성하자
amplitudes = [0.2, 0.4, 1.0, 2.0]
frequencies = [10, 20, 30, 40]

signals = []

for (amp, freq) in zip(amplitudes, frequencies):
  signal = amp * np.sin(freq * 2 * np.pi * time)
  signals.append(signal)

signal = sum(signals)

plt.plot(signal)
plt.show()

위 코드를 통해 얻은 합성파의 모습은 다음과 같다.

FFT 변환하기

Numpy 의 FFT 함수를 이용하여 위 신호를 주파수별 magnitude로 변환해보자

s_fft = np.fft.fft(signal)
amplitude = abs(s_fft)*(2/len(s_fft))
frequency = np.fft.fftfreq(len(s_fft), T)

plt.xlim(0, 50)
plt.stem(frequency, amplitude)
plt.grid(True)
plt.show()

amplitude(진폭)을 구하기 위해 절대값을 취하는 것이나, 2 / len(s_fft)로 나누어 주는것은 퓨리에 변환에 대한 조금더 깊은 지식을 설명이 필요해서 여기서는 넘어간다.

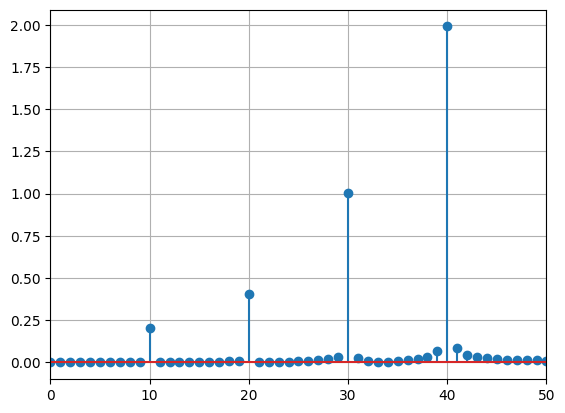
변환된 그래프에서 amplitude와 frequency가 초기 입력한 값과 거의 동일함을 알 수 있다. 40Hz인 파동의 amplitude 가 2.00에 근사한 값을 가지며, 이는 우리가 만든 4번째 주기 데이터에 해당한다.

퓨리에 변환의 의의

소리 데이터를 퓨리에 변환하여 "주파수-위상"으로 나타낸다면, 우리가 원하지 않는 주파수 대역을 지운 뒤 다시 역-퓨리에변환을 통해 "시간-진폭"데이터로 바꿀 수 있다. 이 기술은 MR 제거, 노이즈캔슬링등에 활용된다. 사람 목소리 대역폭만 남기면 MR 제거 오디오가 되는 것이며, 주파수별 반대 위상을 같은 데이터를 실시간으로 출력하면 두 음파를 상쇄시켜 노이즈캔슬링을 구현하는 것이다.

건설 현장의 경우에는, 실제로 사람이 느끼는 소음도를 측정하기 위해 A-가중치를 적용한 소음도를 측정한다. 외의도에서 소리는 굴절되기에 고막에 잘 도달하는 파장이 있고 그렇지 못한 파장이 있다. 더 잘 도달하는 파장(주파수)에 대해서는 더 시끄럽게 들리는 원리이다. 실험적으로 구한 주파수에 따른 소음도 차이인 "A-가중치"를 측정한 "주파수-위상"데이터에 합성하면 사람이 느끼는 소음도 변화를 더 잘 표현할 수 있다.

여담이지만, 지진계에서 측정된 샘플을 퓨리에 변환하여 지하 핵실험과 실제 지진을 구분할 수 있다고 한다.

마치며

푸리에 변환에 대해 공부하면서, 일상속에서 다양하게 활용되고 있다는 사실을 알았다. 더 나아가 STFT(단시간 퓨리에 변환)을 사용해 시간의 흐름에 따라 변하는 소리를 분석하는 방법과 Spetogram으로 나타내 CNN(Convolutional Neural Network)을 결합해 소리의 종류를 구별하는데 사용되는 만큼, 더 깊은 이해가 필요한 개념이라고 생각한다.