3차시 - 손실 함수와 최적화
1. Loss Functions
손실함수는 w을 입력으로 받아서 각 스코어를 확인하고 이 w가 얼마나 별로인지 알려준다.

각 스코어는 Wx의 값이다. 각 사진이 제대로 잘 분류되었으면, 고양이는 고양이의 스코어가, 차는 차의 스코어가, 개구리는 개구리의 스코어가 가장 높아야 한다. 하지만 위의 결과를 보면, 고양이 사진에서는 차 스코어가 더 높고, 개구리 사진에서는 오히려 개구리 스코어가 가장 낮음을 알 수 있다. 손실함수는 이러한 결과를 나오게 한 W가 얼마나 별로인지를 알려주는 지표이다.
1. Multiclass SVM Loss
먼저 손실함수의 종류에는 Multiclass SVM Loss가 있다.

개구리 사진의 스코어로 계산을 해보면, 위의 식과 같다. 자기 자신의 값을 더하게 되면 Loss의 최소값이 0이 아니라 1이 되기 때문에 자기 자신의 값을 제외하고 계산을 해준다.

계산을 하면, 위의 Wx의 Loss는 5.27이다.
교수님께서는 몇가지 질문들을 통해 헷갈리는 개념들을 정리했다.
1) 차의 스코어를 조금 바꾸면 Loss의 값이 바뀌는가?
-> 바뀌지 않는다. 마진인 1보다 더 차이가 난다면, 여전히 답은 0이 나올것이다.
2) 가능한 최솟값과 최댓값은 얼마인가?
-> 최솟값은 0이고, 최댓값은 무한대이다.
3) W가 너무 작아서 스코어들이 거의 0이 나온다면?
-> Loss는 C-1이 나올 것이다. 왜냐하면 정답이 아닌 클래스를 순회하는데 마진이 1이기 때문에 둘 다 0에 가까운 값을 가진다면 결과로 1이 나올 것이기 때문이다. 이 방법은 디버깅을 할 때 유용하다고 한다.
4) Loss들의 합이 아닌 평균을 구한다면?
-> 스케일의 차이만 생길 것이다.
5) 제곱을 한다면?
-> 아마 곱절로 나쁜 값이 나오기 때문에 얼마나 별로인지 더 확연하게 드러날 것이다.
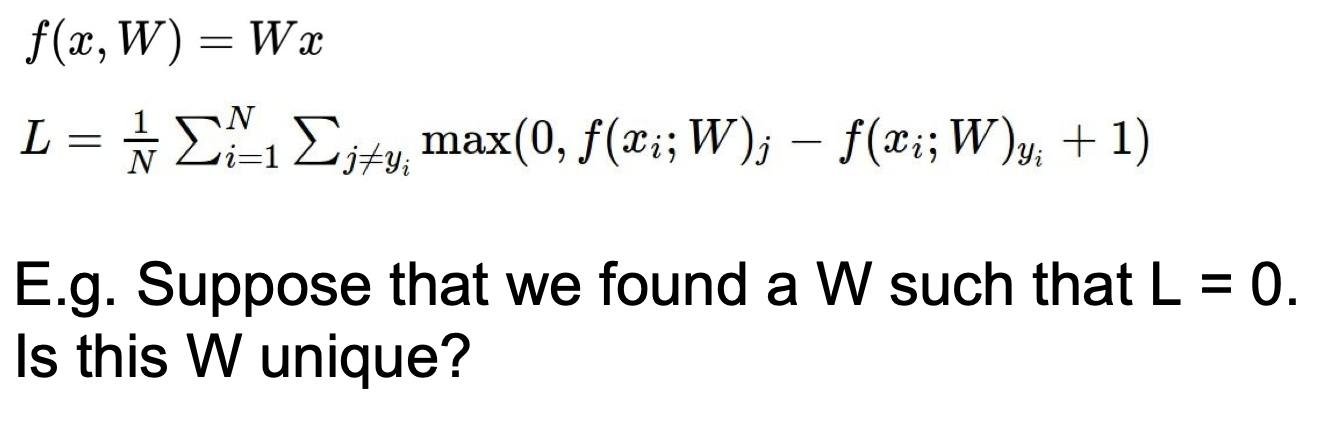
Loss가 0인 W는 하나인지에 대한 고민을 해봤을 때 쉽게 아니라는 것을 알 수 있다. 2W의 Loss도 0이기 때문이다. 물론 2W 말고도 Loss가 0인 W는 수없이 많을 것이다.

Loss가 0이 되도록 훈련을 한다면, 자칫 잘못했다가 위의 그림과 같이 직선이 아닌 훈련한 데이터에만 맞는 곡선이 나올 수가 있다. 이를 방지하기 위해 Regularization(규제)를 해준다.
규제에는 전차시에서 배운 L1 또는 L2, Elastic net(L1 + L2), Max norm regularization, Dropout, Batch normalization, stochastic depth 등이 있다.

강의에서는 L1과 L2의 차이점을 다뤘다. x와 w1을 내적한 값과, x와 w2를 내적한 값은 둘 다 1로 같다. 하지만 L2는 w2를 선호하며, L1은 w1을 더 선호한다. L2는 더 매끄러운 것, 즉 값이 균등한 것을 선호하는 반면, L1은 0이 많은 것을 선호하기 때문이다.
2. Softmax Classifier
다음은 소프트맥스이다. Multiclass SVM Loss는 상대적으로 올바르게 분류한 스코어가 높은지를 봤다면, 소프트맥스는 절대적으로 올바르게 분류한 스코어가 좋은 지를 판단한다.

스코어들을 모두 제곱한 다음 0과 1사이로 정규화를 해주고 올바르게 분류한 스코어의 값을 -log 해주면 된다.
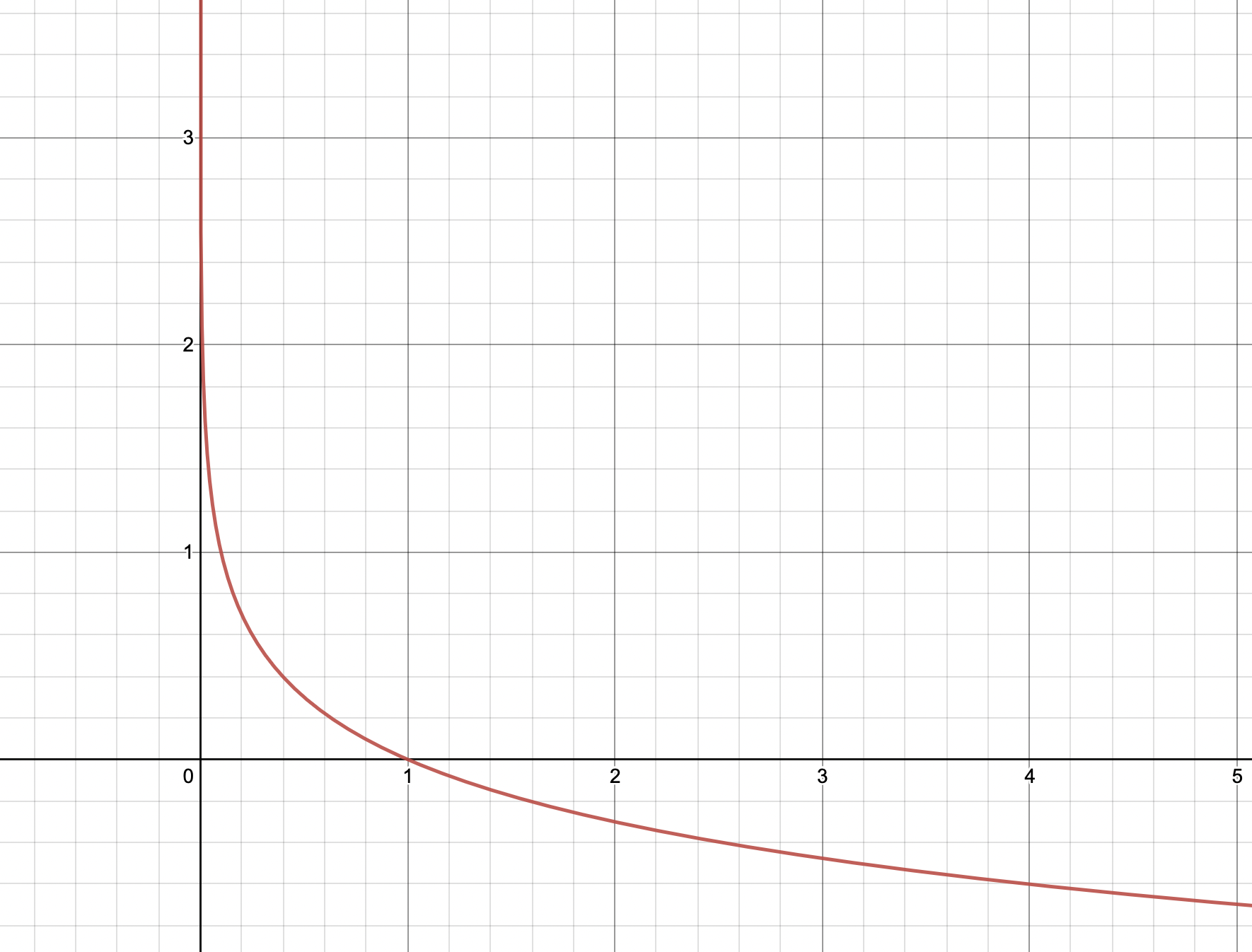
-log의 그래프는 x의 값이 0에 가까울수록 y 값은 무한대로 커지고 x가 1일 때 y 값이 0임을 알 수 있다. 정규화까지 마친 값이 1에 가까울수록 스코어가 높은 것이므로 Loss는 0에 가깝고, 0에 가까울수록 스코어가 낮은 것이므로 Loss는 더 커지므로 이를 나타내기 위해 -log를 해준다.
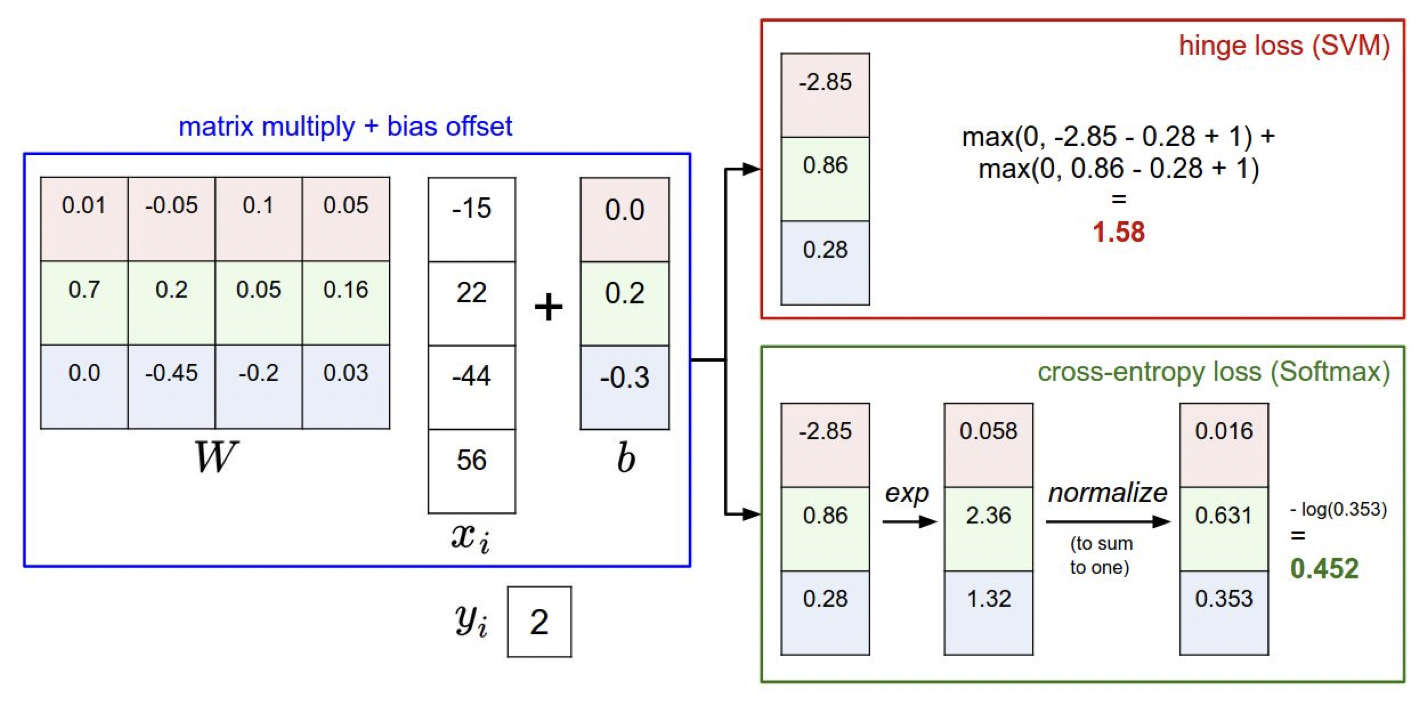
두 방법을 이용해 계산한 과정은 위의 그림과 같다.
SVM과 Softmax의 가장 큰 차이점은 SVM은 어느 수준을 넘으면 더이상 좋아지려고 하지 않는 반면 Softmax는 계속 더 좋아지려고 한다는 것이다. SVM은 오직 정답과 그 외 클래스의 마진이 얼마나 되는지에만 관심있고 Softmax는 정답 스코어가 충분히 높고 다른 클래스의 스코어가 낮아도 최대한 정답 클래스에 몰아넣으려는 특징이 있기 때문이다. 하지만 실제로 두 개를 사용했을 때 비슷한 결과가 나온다고 한다.
2. Optimization
최적화는 Loss가 낮은 W를 찾는 과정을 말한다. 랜덤하게 돌려서 찾는 방식과 경사를 이용한 방식이 있다. 경사는 산에서 내려갈 때 지금 경사를 보고 낮은 쪽을 향하는 방식과 같다.
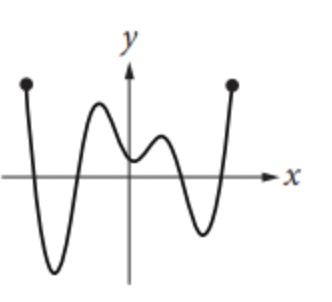
위의 그림에서 Loss가 가장 낮은 지점을 찾자면,
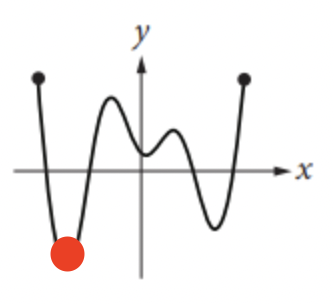
빨간점으로 표시한 지점의 값이 가장 낮을 것이다. 그 때의 기울기는 0이므로 기울기가 0이 될때까지 기울기의 반대방향으로 조금씩 이동한다는 이론이다.
그림같은 경우에는 수많은 픽셀로 이루어져 있기 때문에 경사를 도출해내기 위해 매번 모든 데이터들을 미분하는 것은 오랜 시간이 걸린다. 그래서 나온것이 SGD, Color Histogram, Histogram of Oriented Gradients(HoG), BoW이다.
간단하게 설명하면, SGD는 확률적으로 데이터들의 일부분만 뽑아서 계산을 하는 방식이며, Color Histogram은 이미지에 들어간 컬러들의 갯수를 세서 분류한 방식이며, HoG는 지역 안에서의 방향을 찾아서 나타내는 방식이며, BoW는 RNN에서 착안한 방식으로 이미지 조각들을 모아서 비교하는 방식이다.
키워드 : Loss Function(손실 함수), SVM, Softmax, Regularization(규제), Optimization(최적화), SGD, Color Histogram, HoG, BoM
