4차시 - 오착역행렬과 인공신경망
1. Backpropagation(오차역행렬)
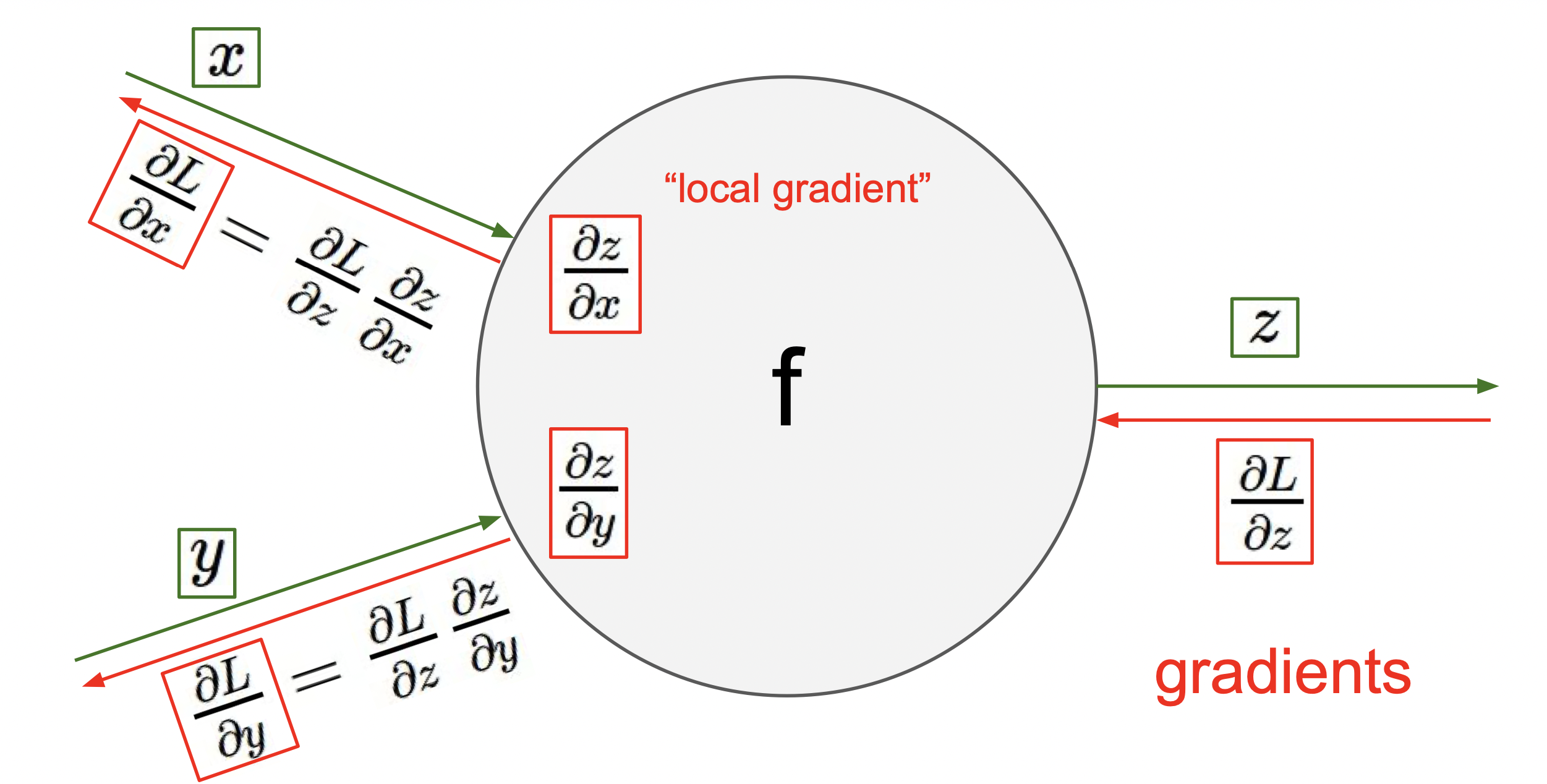
오차역행렬의 주요 개념은 위의 그림과 같다.
∂x∂L=∂z∂L*∂x∂z이므로 그 전의 계산을 통해 구한 ∂z∂L와, ∂x∂z을 곱해서 ∂x∂L을 구한다.
이렇게 말하면 잘 이해가 가지 않을 수 있다. 더 풀어서 설명을 하면 다음과 같다.
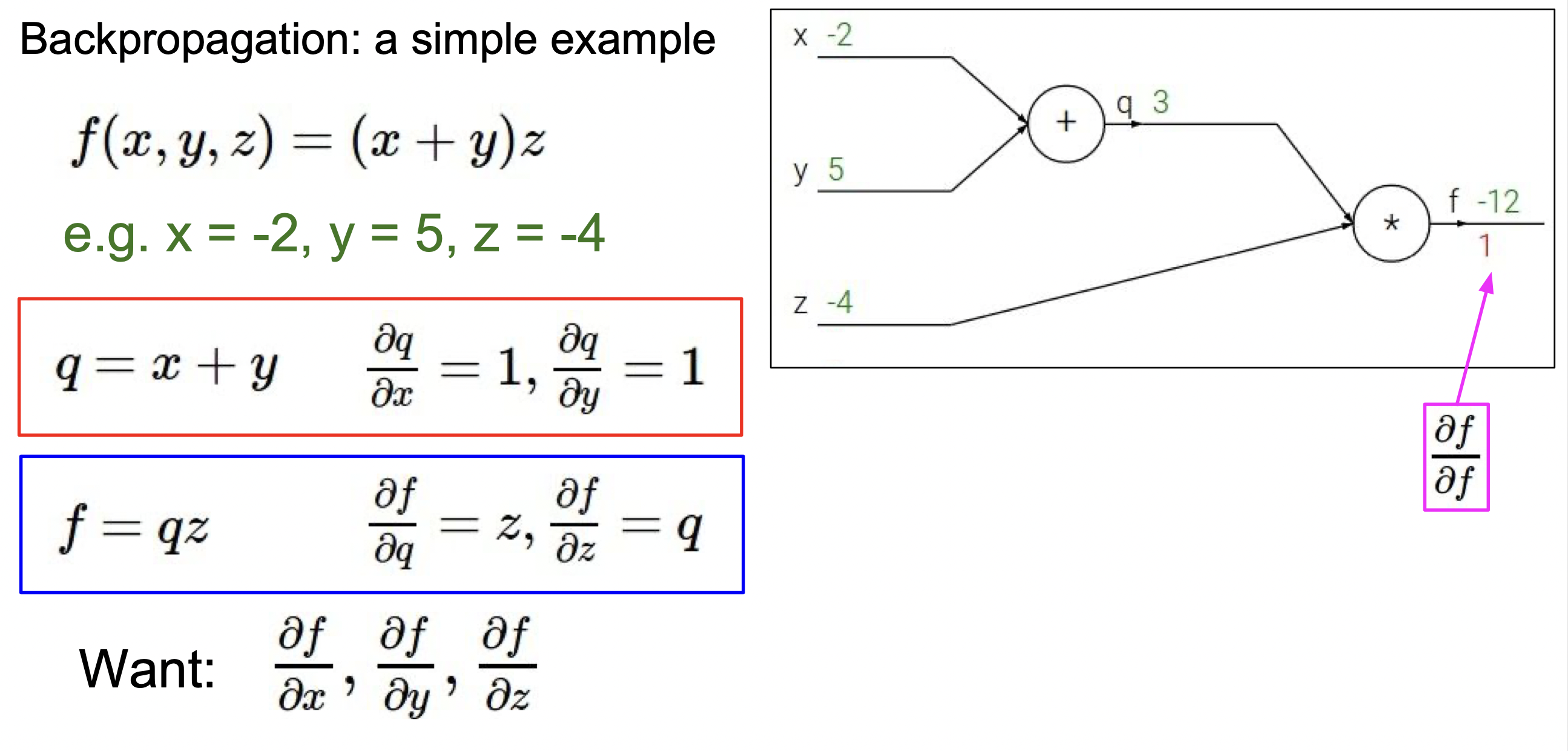 q = x + y 식에서 각각 x와 y에 대한 도함수를 구하면, 둘 다 1의 결과가 나온다.
q = x + y 식에서 각각 x와 y에 대한 도함수를 구하면, 둘 다 1의 결과가 나온다.
또한, f = (x+y)z = qz의 식에서 각각 q와 z에 대한 도함수를 구하면 z와 q의 결과가 나온다.
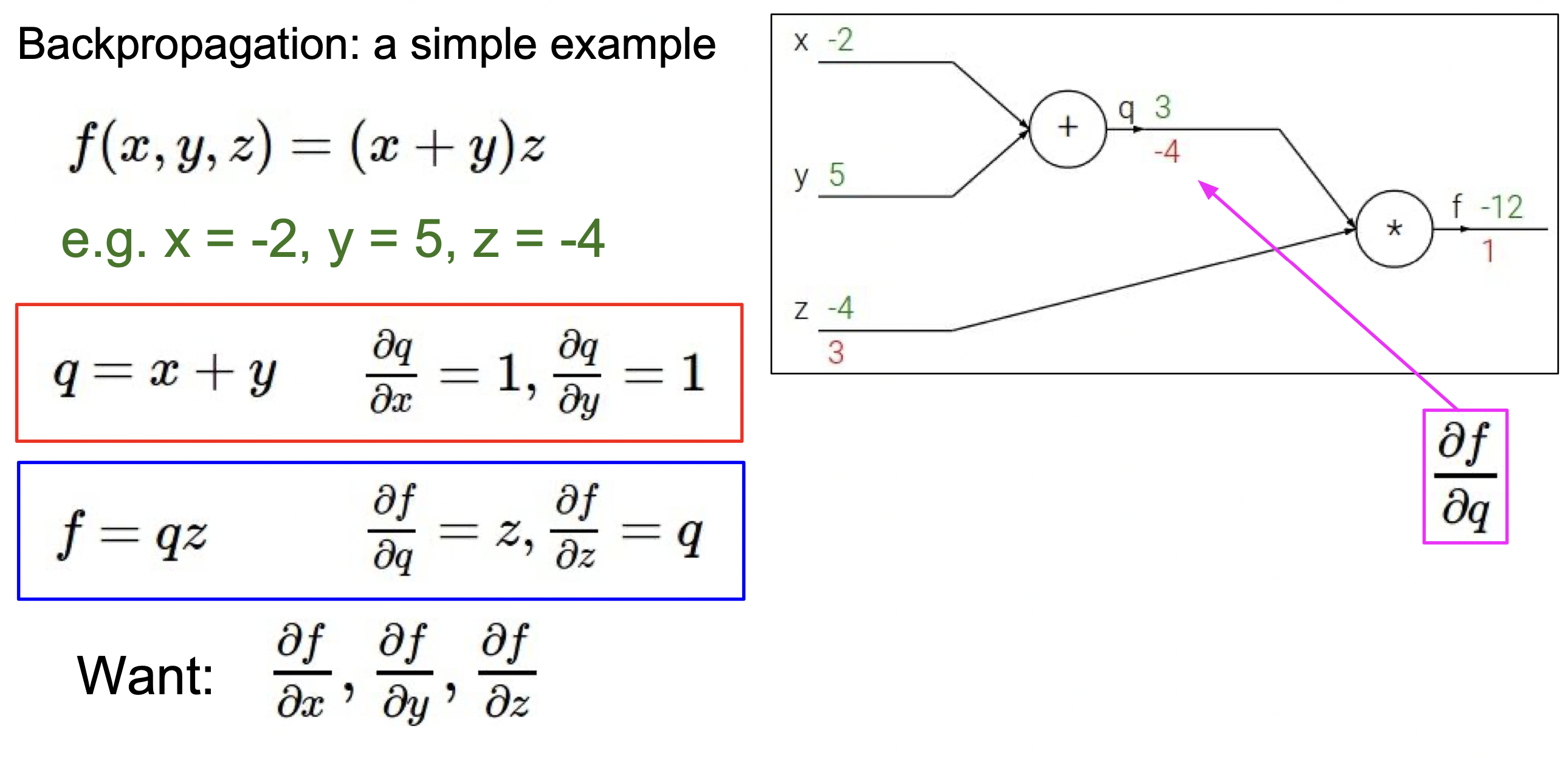
∂q∂f = z 이고, ∂z∂f = q이므로 각각 3과 -4의 값을 가진다.
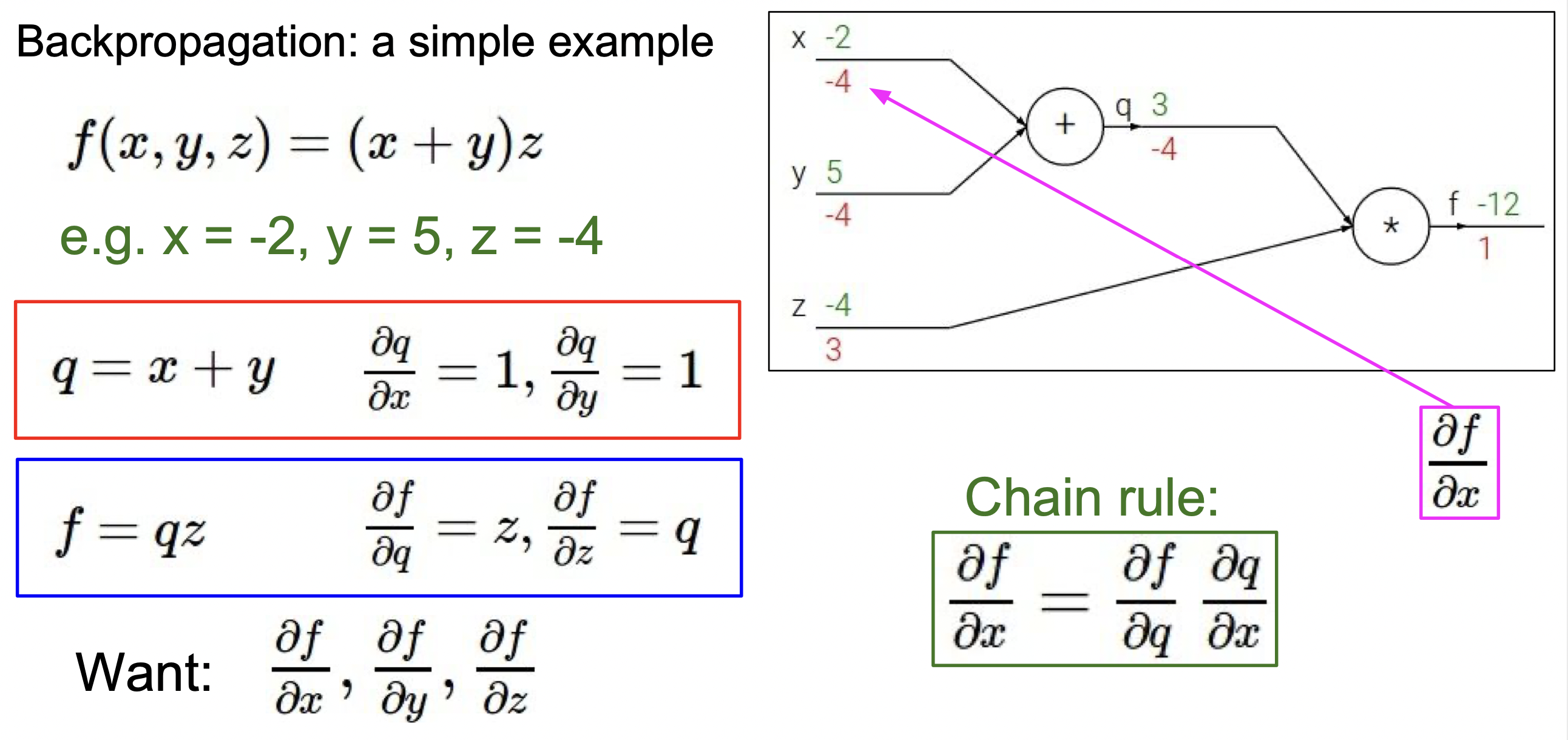
그 다음 단계에서 Chain rule이 쓰인다. 위의 식을 보면 바로 -4*1을 통해 ∂x∂f 와 ∂y∂f가 -4임을 알 수 있다.
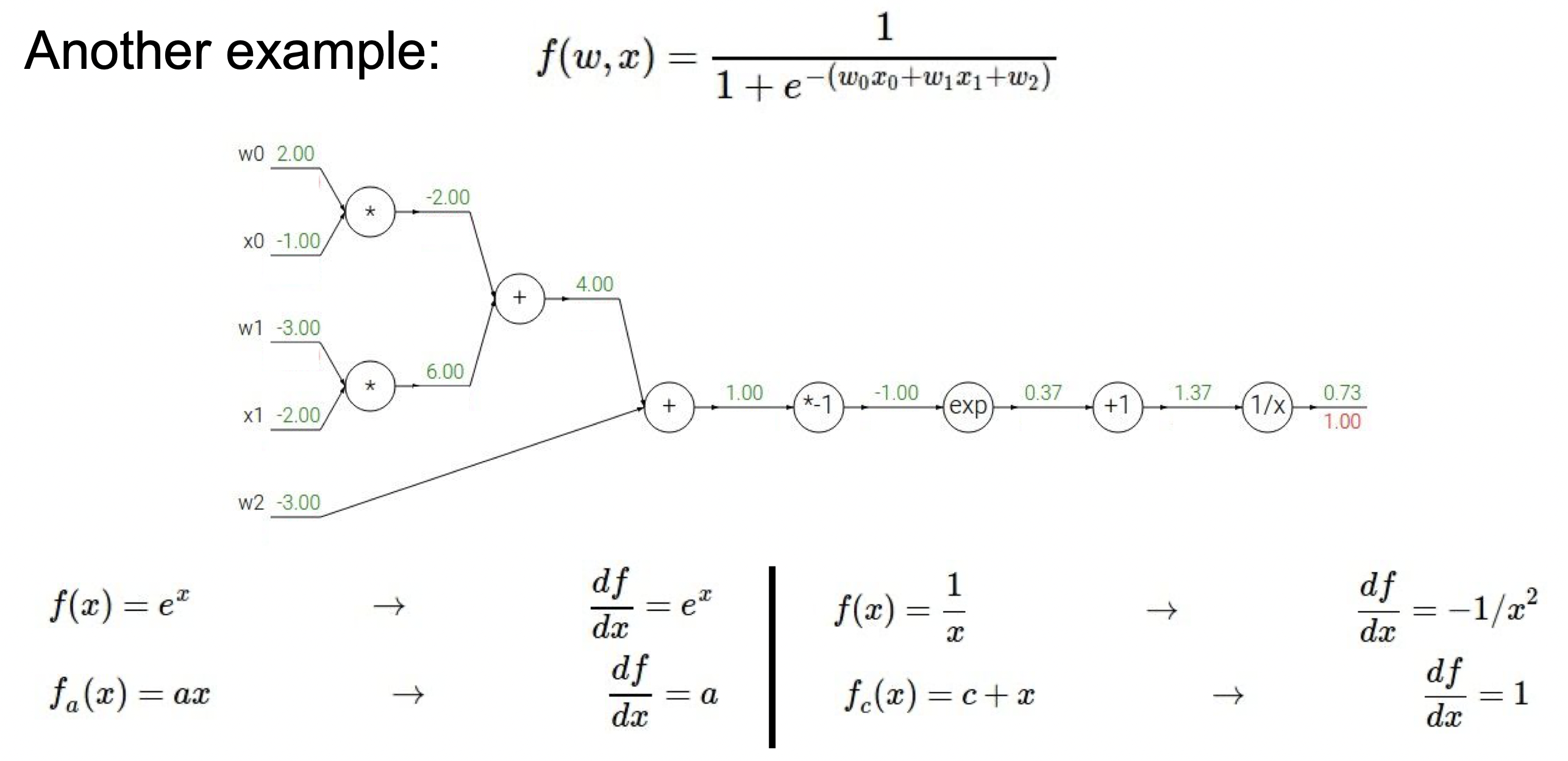
다른 예시를 보면, 아래에 미리 미분 값을 나타냈다. 처음부터 ∂f∂f = 1 부터 시작하면, 1/x 의 미분 값이 -1/ x^2 이므로 (1.372−1)(1.00) = -0.53이 나온다.
이렇게 차례대로 하다 보면 다음과 같은 결과가 나온다.
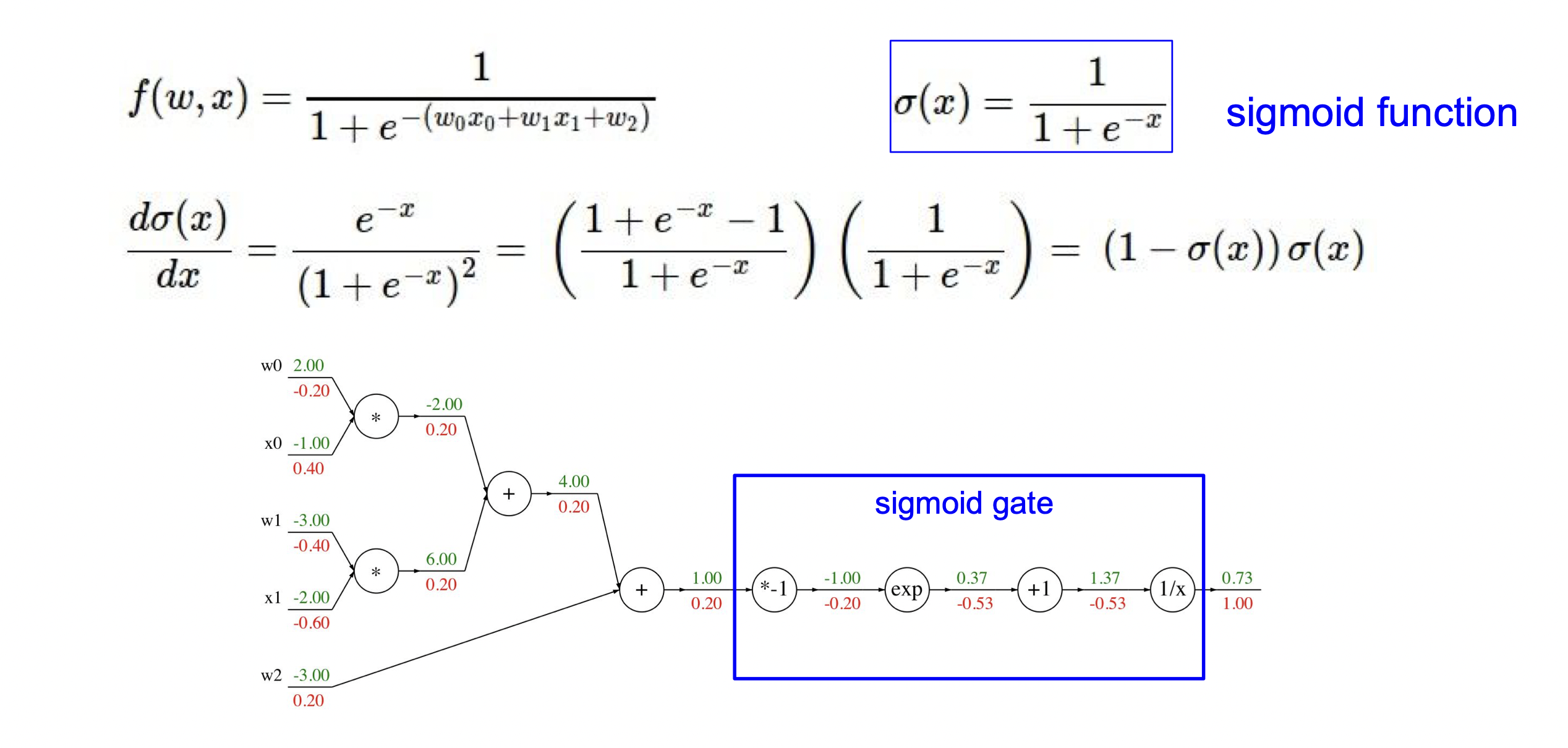
또한, 파란 네모를 친 수식을 합치면 시그모이드 함수가 되는데, 간단하게 묶어서 계산을 해도 똑같은 결과가 나온다.
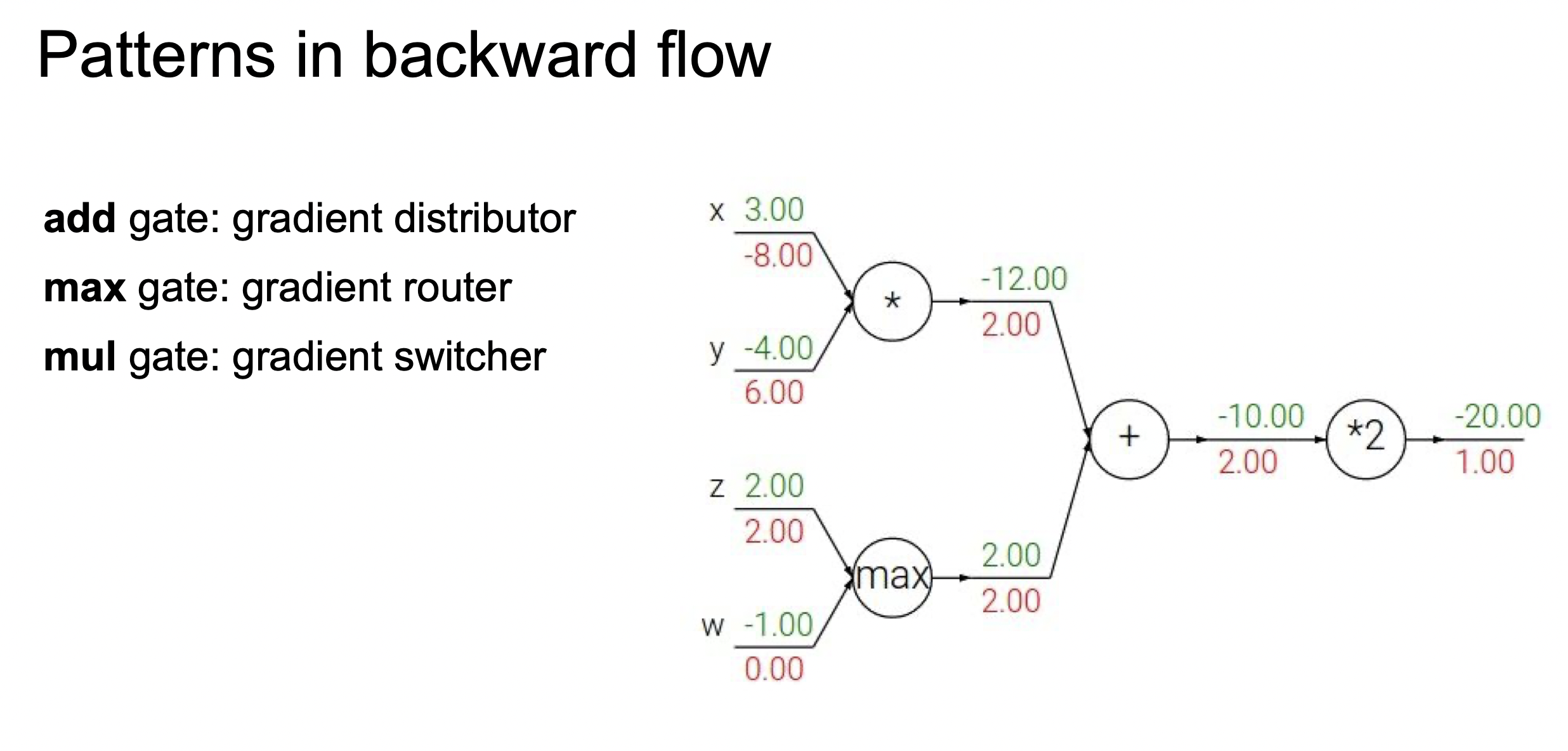
add는 오차역행렬을 했을 때 값이 변하지 않으며, max는 둘 중 더 큰 값에만 적용하며, mul은 서로 바꿔준다는 특징이 있다.
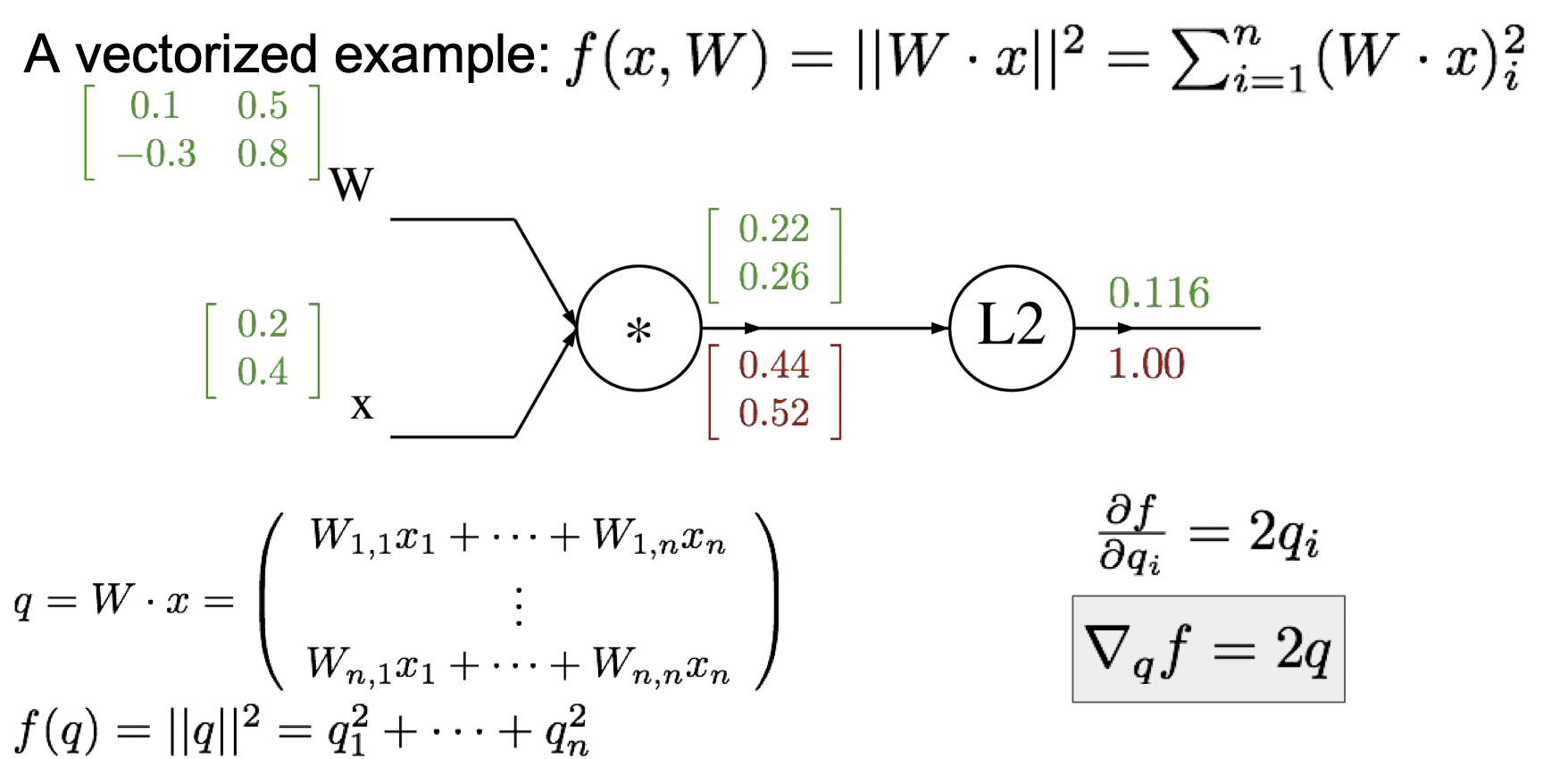
다음은 야코비행렬 예제이다. f(x,W)의 식에서 Wx를 q로 치환하고, q에 대해서 미분하면 2q가 나온다. 따라서 [0.220.26] 에 2를 곱하면 [0.440.52]가 나온다.
다음은 행렬곱을 하기 때문에 다소 어렵다. 주요 개념은 영향을 주는 요소들만 계산해준다는 것이다.
[W1,1W2,1W1,2W2,2] [x1x2] =[W1,1x1+W1,2x2W2,1x1+W2,2x2]
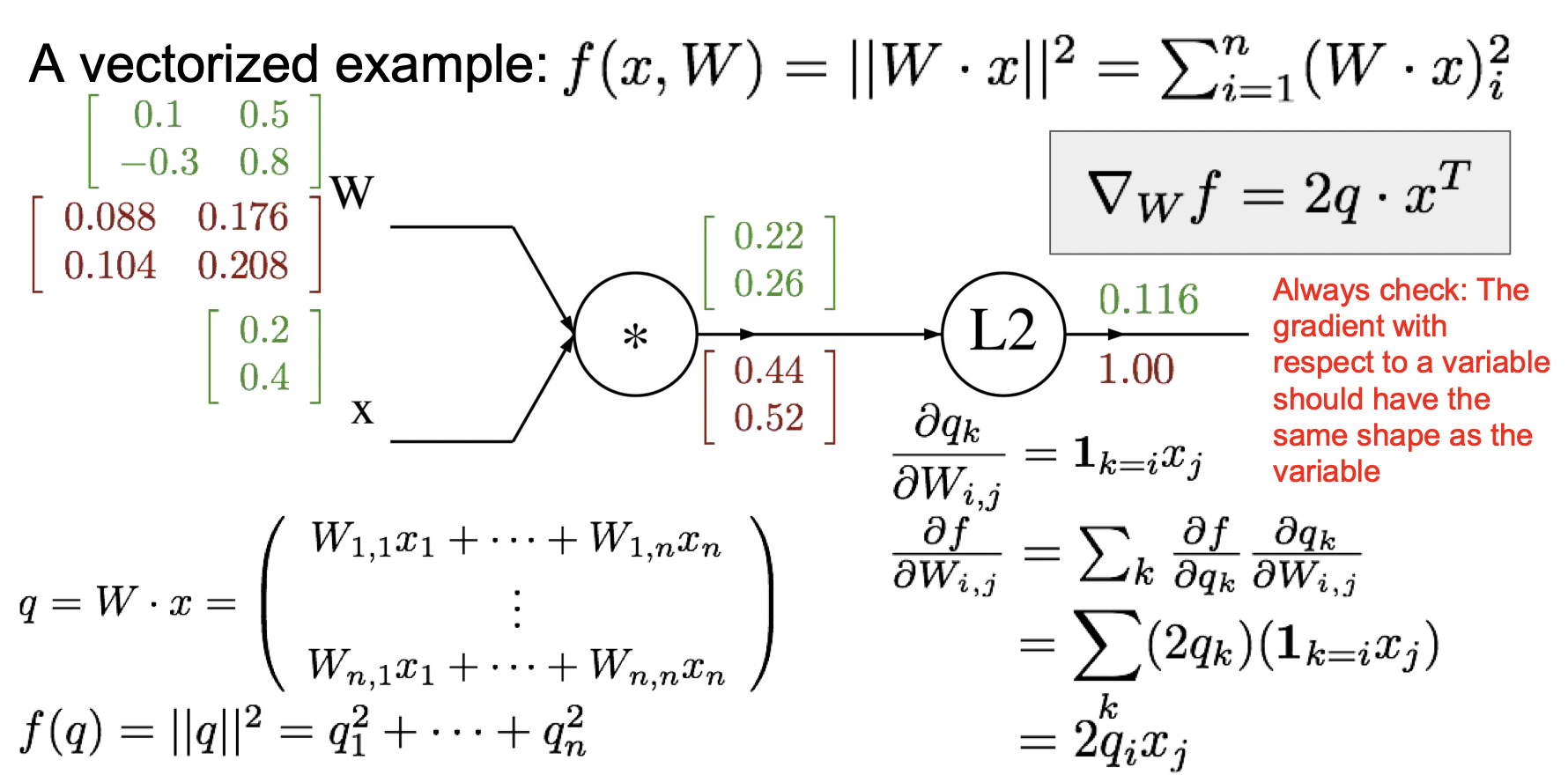
먼저, Wx를 W로 미분해주면 xT라는 값이 나오기 때문에 ∂W∂f=∂q∂f∂W∂q =2qxT이다. 계산하면, [0.440.52] [0.20.4] = [0.0880.1040.1760.208] 이 나온다.
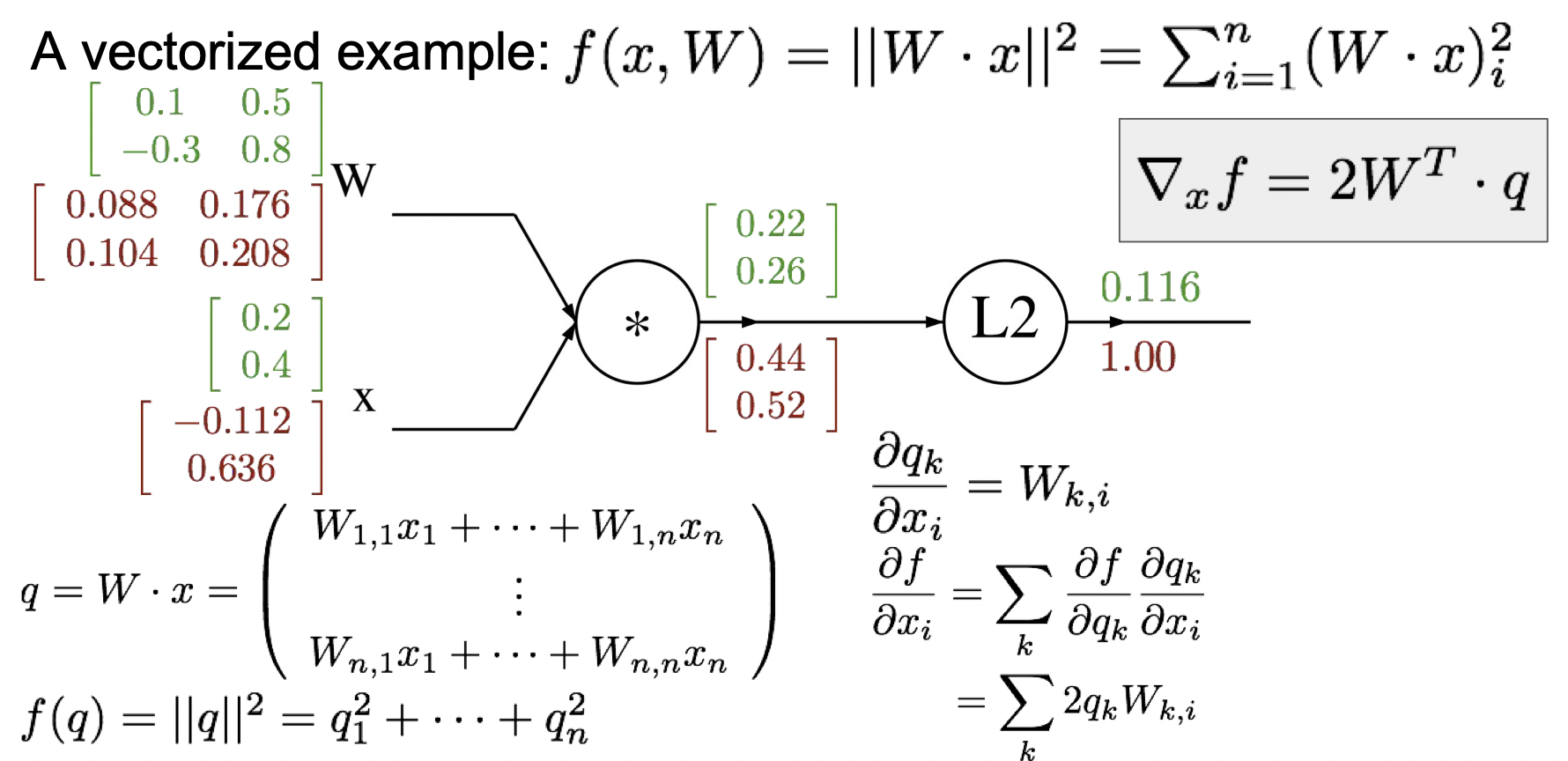
Wx를 x로 미분해주면 WT라는 값이 나오기 때문에 ∂x∂f=∂q∂f∂x∂q =2WTq이다. 계산하면, [0.10.5−0.30.8 ] [0.440.52] = [−0.1120.636] 이 나온다.
2. Neural Networks (인공 신경망)
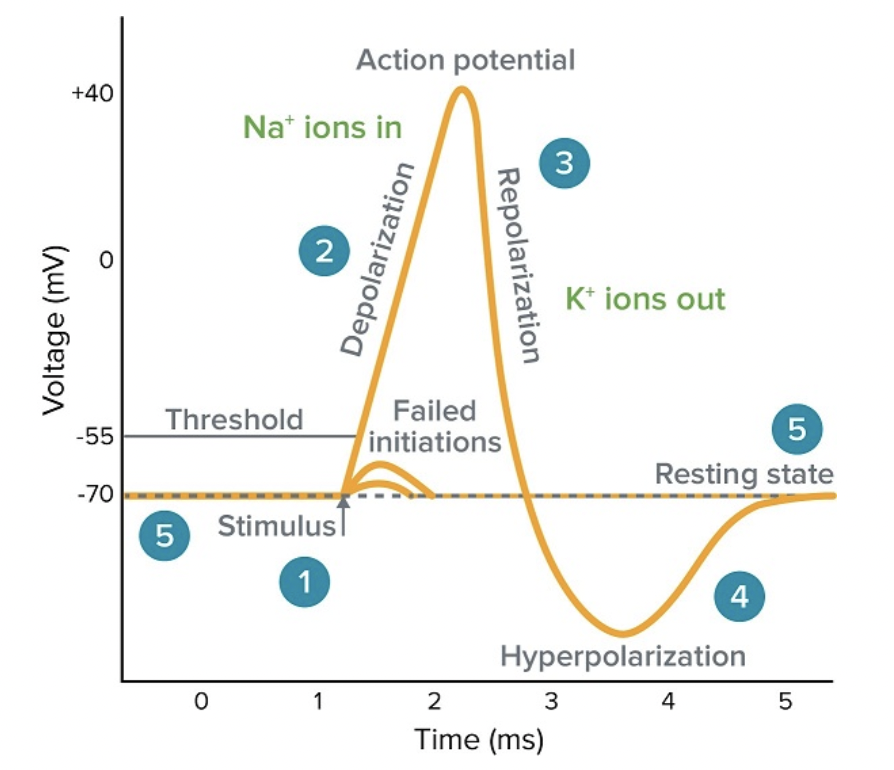
출처: ko.moleculardevices .com
뉴런에서 흥분을 전도하기 위해서는 역치 전압 이상의 전압이 필요하다. 역치 이하의 전압에서는 자극을 전달하지 못하고 휴지 전위 상태를 유지하게 된다.

인공 신경망은 이러한 개념에서 착안해서 선형 변환과 비선형 변환을 둘 다 하도록 설계 한다.
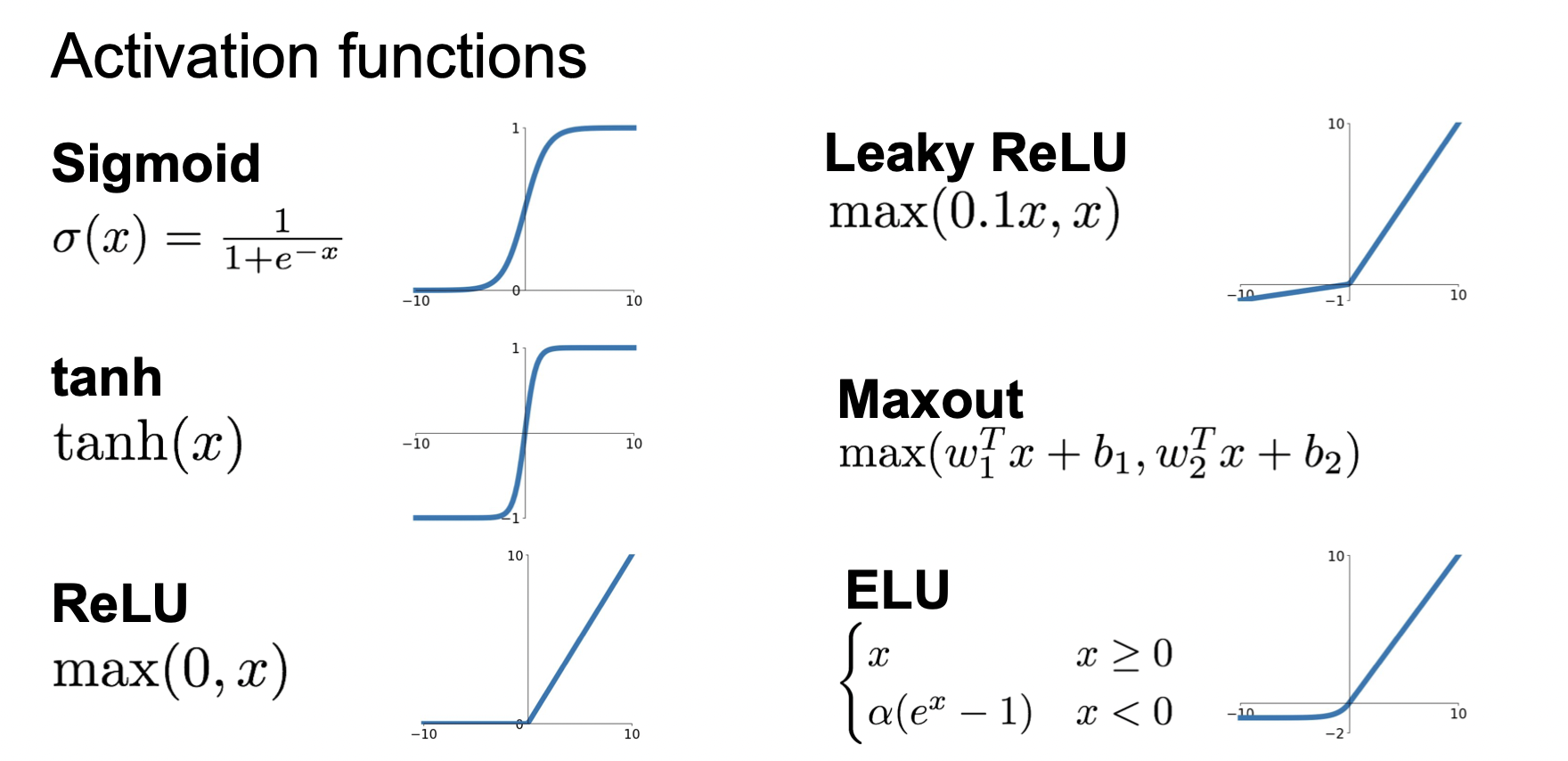
비선형 변환을 하는 활성화 함수에는 여러가지 종류가 있다. Sigmoid, Leaky ReLU, tanh, Maxout, ReLU, ELU등이 있다.
키워드 : BackPropagation(오차역행렬), 야코비행렬, Neural Networks(인공 신경망), 활성화함수

 q = x + y 식에서 각각 x와 y에 대한 도함수를 구하면, 둘 다 1의 결과가 나온다.
q = x + y 식에서 각각 x와 y에 대한 도함수를 구하면, 둘 다 1의 결과가 나온다.










