211207, 자료구조 Ch.08-3

about Expression Tree

08-4

이진 트리의 일종인 수식 트리를 공부해보자.

수식 트리란 뭐냐. 이름 그대로 생각하면 된다. "수식을 트리로 표현한 것"이다. 이 때 쓰이는 "트리"가 이진트리고. 그래서 그냥 이진 트리를 활용한 하나의 예시라고 생각해도 된다.

예를 들면, 7 + 4 * 3 - 1 이라는 수식이 있다.

근데 컴퓨터가 이걸 스스로 인식하는건 정말 편한거긴 하다. 그런데 혹시 모를 오류를 범하긴 싫으니까, 가급적이면 처음 코드를 짤 때 컴퓨터의 유연한 판단을 우리가 도우는게 더 좋지 않을까? 그래서 수식 트리를 활용한다.

위의 수식 예시를 수식 트리로 짜면 어떻게 될까?

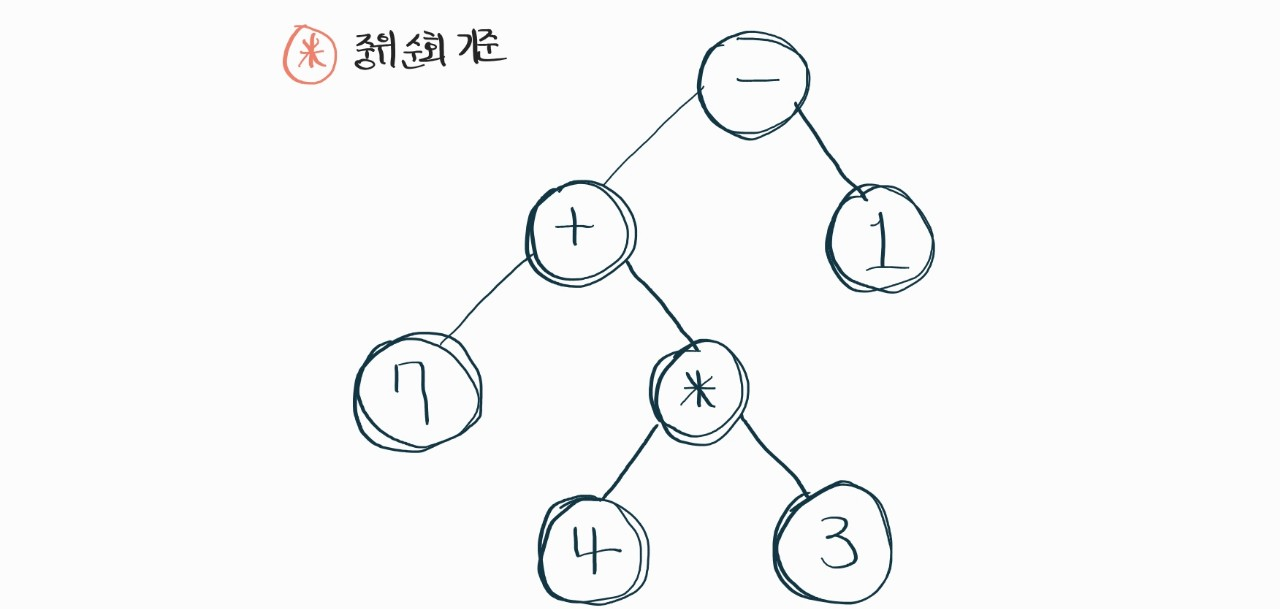
이렇게 된다. 왼쪽부터 차근차근 중위순회 생각하면서 가보면 위의 수식과 같이 계산이 될 것이다.

그냥, 수식을 표현하는 방법 중에 하나라고 생각하면 된다.

위 그림을 보면 수식 트리의 특징이 보일꺼다.

"루트 노드에 저장된 연산자의 연산을 하되, 두 개의 자식 노드에 저장된 두 피연산자를 대상으로 연산을 함."

• 엥 그런데 4*3은 뭔데요? 자식 노드가 연산자인데요?

저건 4x3을 하면 x의 자리에 12가 있다고 생각해주면 된다. 그러면 7 + 12가 되겠지. 고런 넉김.

여기서 우리가 중위 표기법을 그대로 수식트리로 표현하는건 복잡하다. 막 복잡하게 연산자들이 섞여있는 계산이라면, 그거의 순서를 구현한다는게 꽤 머리가 아픈 일일거다.

그래서 이 교재에서 저자는 중위 표기법 -> 후위 표기법 -> 수식 트리 과정으로 수식 트리를 만들어 나간다.

어? 순회법이 아니고 표기법 간의 변환? 어디서 봤지 않나?

자. 그러면 얘들을 통틀어서 InToPost를 구현해 보겠다. 되게 복잡하고 어렵게 생겼지만, 차근차근 주석을 보며 이해해나가자.
.. 자료구조 Ch 06-2에서

글렇다. 우리가 신경 써줄건 후위 표기법을 수식 트리로 바꿔주는 과정만 신경써주면 된다.

그리고 이 과정에서 Stack을 필요로 하는데. 우린 스택도 이전에 공부를 하면서 헤더파일과 이를 구현한 소스파일을 만들어 놨다. 이것도 그냥 활용하자.

심지어 이진 트리를 구현하 헤더파일도 만들어 놨다. 뭐 다했네 ㅋㅋ

.. 가 아니고, 수식 트리 표현을 위한 파일을 만들어 보겠다.

/* ExpressionTree.h */

#ifndef __EXPRESSION_TREE_H__
#define __EXPRESSION_TREE_H__

#include "BTree.h" // Ch.08-2 복습 내용 확인

BTreeNode *MakeExpTree(char exp[]); // 수식 트리 만들기
int EvaluateExpTree(BTreeNode *bt); // 수식 트리 계산

void ShowPrefix(BTreeNode *bt); // 전위 표기법 기반 출력
void ShowInfix(BTreeNode *bt); // 중위 표기법 기반 출력
void ShowPostfix(BTreeNode *bt); // 후위 표기법 기반 출력

#endif

여기서 MakeExpTree 앞에 포인터가 위치하는데, 이건 수식 트리를 완성하고 난 뒤, 그 트리의 주소값을 반환하기 위해 포인터가 있다. 정확히는 Root Node의 주소 값을 반환하는거다.

EvaluationExpTree는 뭐 말 그대로다. 수식 트리를 계산한다.

그러면, 후위 표기법 수식 기반으로 수식 트리를 구성하는 코드를 짜보자.

일단, 어떤 원리로 트리를 구성할 것인지를 설명하고, 코드를 짜보겠다.

후위 연산자의 특성 두가지를 기억하자.

• 연산 순서대로 왼쪽 -> 오른쪽으로 연산자가 나열
• 해당 연산자의 두 피연산자는 연산자 앞에 나열.

예를 들어서, " 1 2 + 7 * "를 들겠다.

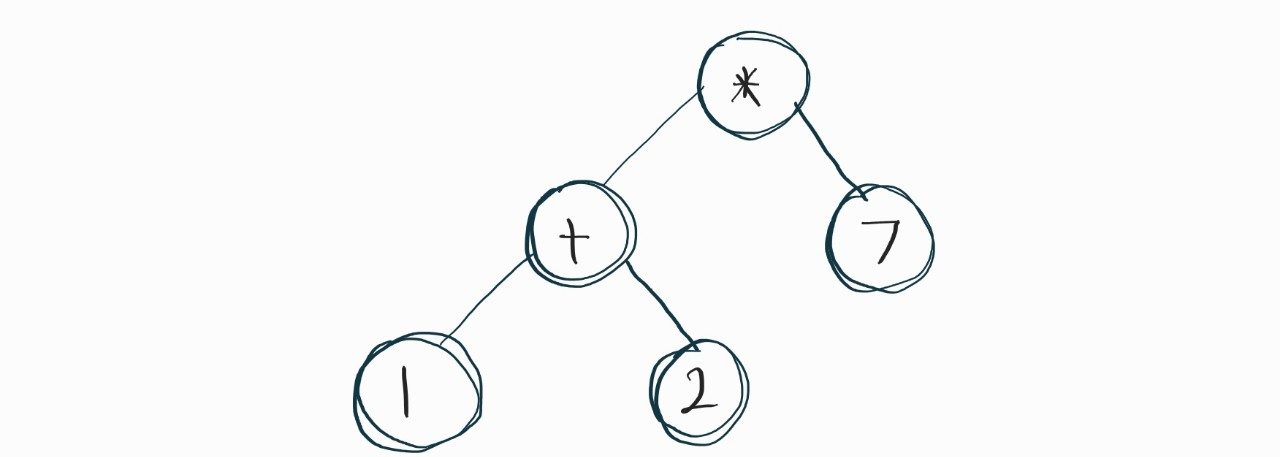
트리로 구성하면, 아래와 같은 구조로 될 것이다.

그러면, Stack을 예로 들어서 생각해보자.

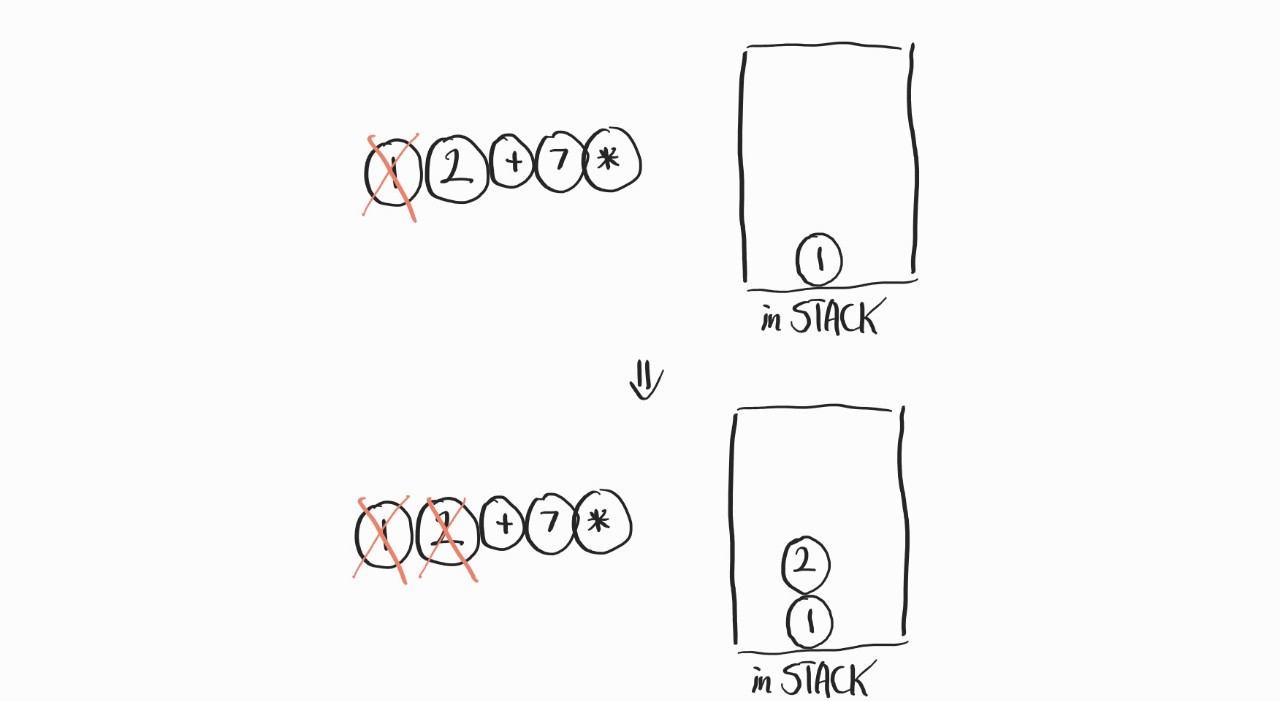
우선, 위처럼 1과 2를 먼저 STACK에 쌓아준다. 그런데, 그 다음엔 연산자가 나온다. 어떻게 될까.

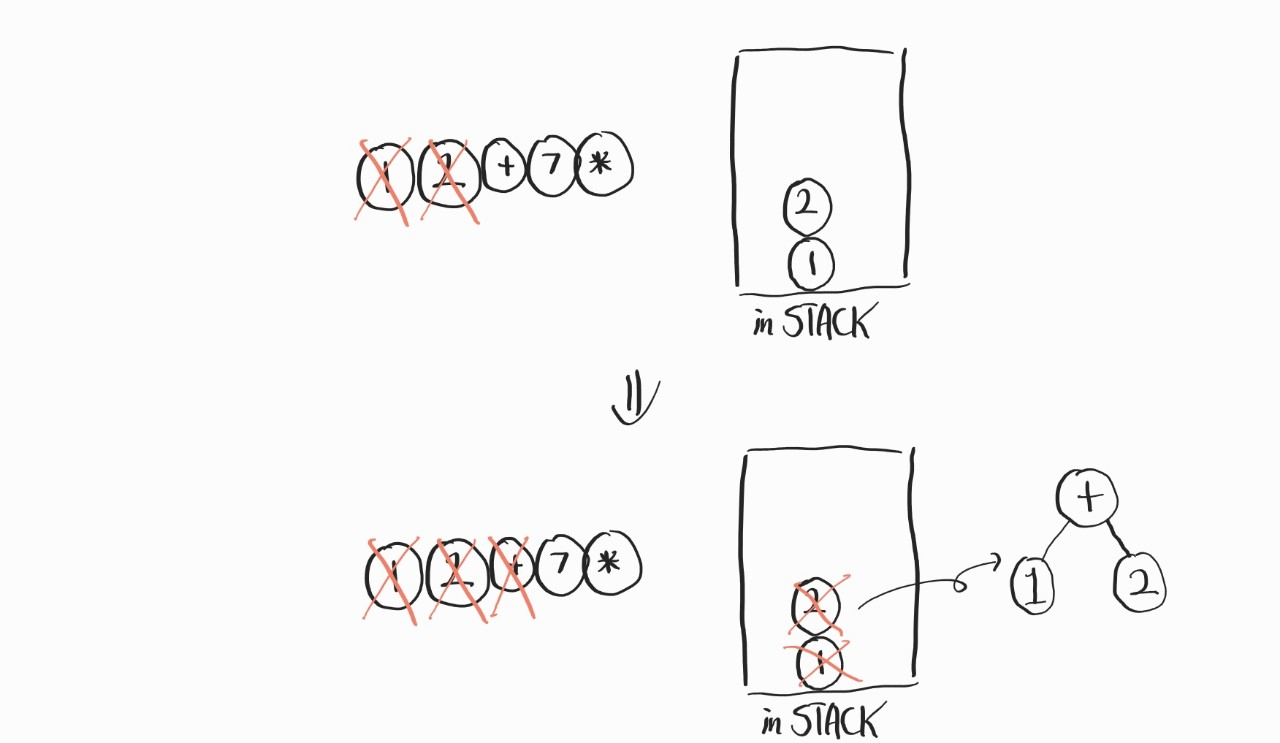
이렇게, +과 함께 쌓여져 있던 피 연산자가 나오면서 SubTree를 하나 만든다.
먼저 뽑혀 나오는 피연산자 A가 오른쪽 node, 이후에 나오는 피연산자 B가 왼쪽 node가 된다. 그 다음은 조금 신기해진다.

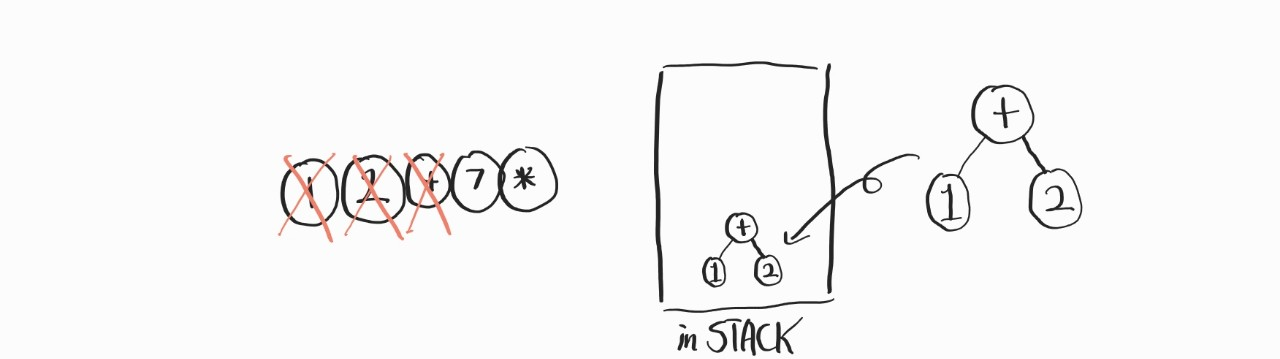
다시 들어간다. 들어간 SubTree를 그냥 하나의 노드라고 생각해주고, 7, *는 앞의 과정을 반복해주면 된다.

그러면, 수식 트리 완성!

• 피연산자를 만나면 무조건 스택으로 옮긴다.
• 연산자를 만나면, 스택에서 두 개의 피연산자를 꺼내 자식 노드로 연결
• 만들어진 SubTree는 다시 스택으로 옮김

이렇게 세개를 기억해두면 된다. 그러면 완성본인 Tree가 Stack에 떡-하니 하나만 놓여져 있게 될거다.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include "ListBaseStack.h"
#include "BTree.h"

BTreeNode *MakeExpTree(char exp[]) {

    Stack stack;
    BTreeNode *node;
    
    int expLen = strlen(exp);
    int i;
    
    StackInit(&stack);
    
    for (i=0 ; i<expLen ; i++) {
    
        if(isdigit(exp[i])) { // 정수라면
            SetData(node,exp[i]-'0'); // 숫자 넣어야지.
        } else { // 연산자라면
            MakeRightSubTree(node, SPop(&stack)); // 우측 node에 숫자 삽입
            MakeLeftSubTree(node, SPop(&stack)); // 좌측 node에 숫자 삽입
            SetData(node, exp[i]); // root node에 연산자 삽입
        }
        
        SPush(&stack, node); // stack에 피연산자 or SubTree 쌓기
    }
	
    return SPop(&stack); // 최종 완성본 트리 반환
}

그렇다.

그리고, 수식 트리를 순회하면서 트리를 전위 / 중위 / 후위 표기법의 수식으로 출력할 수 있는데, 이건 별 거 없다.

앞서 Ch.08-2에서 언급했던 함수 포인터를 사용하면 된다.

바로 코드로 보여주겠다.

/* 헤더파일 */

typedef void (*VisitFuncPtr) (BTData data);
void PreorderTraverse(BTreeNode *bt, VisitFuncPtr action);
void InorderTraverse(BTreeNode *bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode *bt, VisitFuncPtr action);

void ShowPrefix(BTreeNode *bt);
void ShowInfix(BTreeNode *bt);
void ShowPostfix(BTreeNode *bt);

/* 소스파일 */

void ShowNodeData(int data) {
    if (0<=data && 9>=data) {
        printf("%d ", data);
    } else {
        printf("%c ", data);
    }
}

void ShowPrefix(BTreeNode *bt) {
    PreorderTraverse(bt, ShowNodeData);
}

이하 다 비슷비슷..

이런 식으로.

그리고 마지막으로, 구현한 수식 트리를 통해 계산을 하는 함수를 만들어야한다.

밑의 코드를 확인해보자.

int EvaluationExpTree(BTreeNode *bt) {

    int op1, op2;
    
    if (GetLeftSubTree(bt)==NULL && GetRightSubTree(bt)==NULL) {
        return GetData(bt);
    }
    
    op1 = EvaluateExpTree(GetLeftSubTree(bt));
    op2 = EvaluateExpTree(GetRightSubTree(bt));
    
    switch(GetData(bt)) {
        case '+' :
            return op1 + op2;
            .
            .
            .
    }
    
    return 0;

}

여기서 꼭 알아둬야할 부분은 두개다.

우선,

if (GetLeftSubTree(bt)==NULL && GetRightSubTree(bt)==NULL) {
        return GetData(bt);
    }

이 수식. 뭘 위해 존재하는걸까?

어떤 root node의 왼쪽과 오른쪽이 비어있으면 그냥 해당 rootnode값을 반환한다는 의미다.

숫자가 있는 단말노드를 생각해보자. 해당되는 얘기 아닌가?

그렇다. 그냥 숫자가 있는 단말 노드의 경우에는 그냥 그 단말 노드를 해당 값으로 반환한다는 얘기다.

굳이, 왜? 이 의문에 대한 답은 또 아래를 보면 된다.

op1 = EvaluateExpTree(GetLeftSubTree(bt));
op2 = EvaluateExpTree(GetRightSubTree(bt));

op1은 왼쪽 SubTree고, op2는 오른쪽 SubTree다. 그런데, 만약 서브 트리안의 서브 트리가 있는 경우는 그냥 op1값과 op2값을 단순하게 "왼쪽에 있는 값", "오른쪽에 있는 값"으로 치부할 수가 없다. 그래서, 재귀적인 구조를 사용해서, 만약 좌측이나 우측에 다른 계산해야할 subtree가 또 존재한다면 이를 계산하고 그 계산값을 반환하기 위해서 재귀적인 구조를 사용해주는 것이다.

그래서, 이런 코드가 된다.

이 수식 트리를 구현한 모든 소스파일은 내 github에서 확인하자.

여기까지.