Ch.11 탐색(Search) 1
예 전에 Ch 01인가 02에서 탐색에 대해 언급한 적이 있었다. 순차 탐색이랑 이진 탐색 알고리즘을 소개했었다. 하지만, 앞선 정렬처럼 단순한 소개는 아닐 것이다.
일단은, 시작해보자.
11-1
탐색
이름 그대로다. "데이터를 찾는 방법"
이번에 소개할 탐색은 "자료구조"의 맥락에서 보면 되겠다.
그리고, Tree의 연장선상에서 익힌다고 생각하자.
또 하나 더. 지금 우리가 탐색을 하는데, 앞서 정렬에서 했던 것처럼 "성능 평가"라는걸 하게 될거다. 그러면 우리는 "탐색을 효율적으로 하기 위해 어떻게 찾아야 할까?" 만을 고민하는게 아니라, "효율적으로 탐색하기 위해, 처음부터 어떻게 저장을 해야할까?"도 고민해줘야한다.
보간 탐색 (Interpolation Search)
쉽게 한줄로 요약하자면, "이진 탐색의 Upgrade Ver." 이다.
이진 탐색을 공부했던 걸 떠올려보자. 이진 탐색은 처음에 중앙을 잡고, target과의 대소 비교를 하며 탐색을 진행했다.
근데, 애초에 중앙이 아니라 target과 가까운 쪽부터 탐색을 진행한다면?
만약 1 / 2 / 4 / 6 / 7 / 8 / 9 중에서 내가 2를 찾는다고 가정하자. 그냥 이진 탐색 방법이였다면 6을 픽해서 범위를 좁혀나갔을텐데, 처음부터 4나 2를 잡아서 탐색을 진행하면, 최소한 탐색 진행을 한 단계는 줄일 수 있을거다.
즉, 탐색 대상이 앞쪽에 있으면 앞쪽부터 탐색을 시작하고, 뒤쪽에 있으면 뒤쪽부터 탐색을 시작하자는 얘기다.
만약 데이터와 데이터가 저장된 곳의 인덱스 값이 선형으로 비례한다면 ( ex. 오름차순으로 정렬되어있는 배열 ) 단번에 데이터를 찾을 수도 있다.
그림과 함께 설명하겠다.
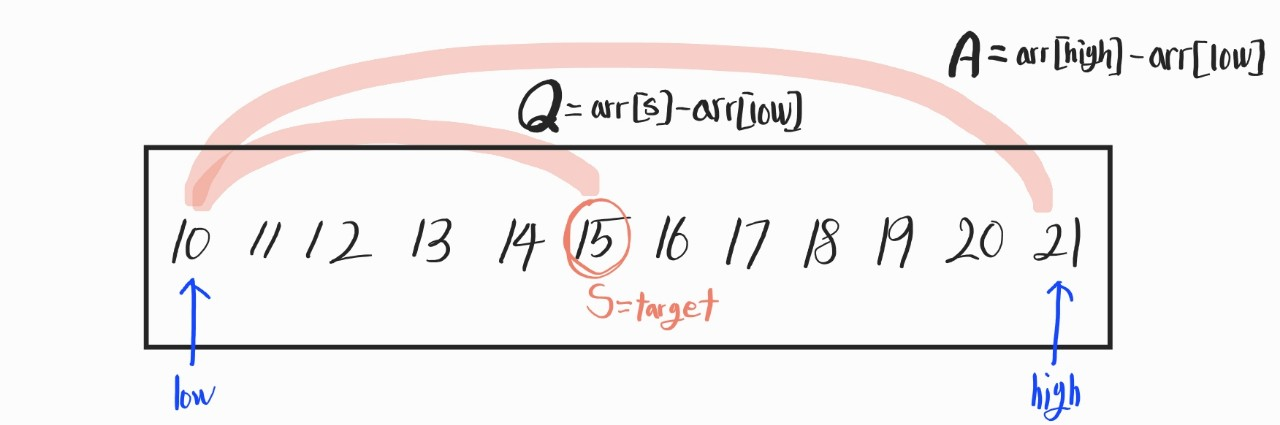
여기서 target은 15고, s는 target의 주소값을 저장한 인덱스 값이라고 가정한다.
low는 탐색대상의 시작, high은 탐색대상의 끝에 해당하는 인덱스값.
여기서 A : Q = high - low : s - low
가 된다.
여기서 우리가 원하는건, s를 알고싶다는거다.
그러면, 위 비례식을 s에 대한 식으로 정리해야하지 않을까?
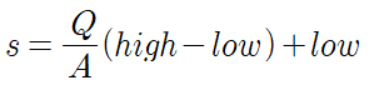
그 다음에, A와 Q에 각각의 값을 더해주고, arr[s]를 임의의 수 x라고 가정하면, 아래와 같이 나타난다.
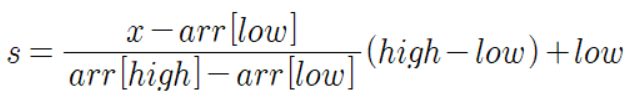
여기서 x (arr[s])에 우리가 찾고자 하는 데이터 (위 그림의 15)를 넣어주면 s의 값, 즉 target의 인덱스값을 찾게 된다.
그런데, 여기선 오차율을 최소화 하기 위해 Q/A를 진행할 때 정수형이 아닌 실수형 나눗셈을 진행한다는 점을 알아두자.
탐색 키(Search key), 탐색 데이터(Search Data)
본격적으로 탐색을 진행함에 있어서, 우리는 이 탐색 키와 탐색 데이터라는 것을 알고 가야한다.
만약 1 ~ 10까지 저장된 배열에서 6을 찾는다고 하자.
솔직히 인덱스값을 찾고싶다고 해도, 만약
이 배열에서 6을 찾자!
라고 막연하게 말하면, 의미가 없다. 6을 가지고 있는데 6을 굳이 왜 찾아야하는지? 생각해보면 할 말이 없다. 그냥 너 잘 있니? 하고 확인하는 느낌밖에 안된다.
그런데, 만약 이렇게 찾는다면?
반에서 6번인 학생의 이름과 성적을 ( = 데이터를 ) 찾아야지!
조금 의미가 생기지 않을까? 그 반에서 고유한 학생의 번호인 "탐색 키"와 우리가 찾고 싶은 "탐색 데이터"가 있다.
그러므로, 우린 탐색의 대상을 "탐색 키"에 맞출것이다.
이 탐색키는, 계좌번호나 사번처럼 "고유해야"한다.
그래도 아마 설명이나 복습은 계속 정수를 찾는 의미 없는 일을 반복할것이다. 우리는 이렇게 "탐색"을 하자!가 아닌, "탐색과 관련된 자료구조의 기본 이론"을 익히자! 니까.
어쨌든, 이 key와 관련된 내용을 코드로 나타내면 이러하다.
typedef int key;
typedef double data;
typedef struct item {
Key searchKey;
Data searchData;
} Item;보간 탐색 구현
#include <stdio.h>
int ISearch(int ar[], int first, int last, int target) {
int mid;
if (ar[first] > target || ar[last] < target) {
return -1;
} // 탐색 대상이 존재하지 않으면, 탐색대상의 값은 탐색범위의 값을 넘어섰다.
mid = ((double) (target - ar[first]) / (ar[last]-ar[first]) * (last-first)) + first;
// 위의 s에 대한 식과 같은 말이다.
if (ar[mid] == target) {
return mid;
} else if (target < ar[mid]) {
return ISearch(ar, first, mid-1, target);
} else {
return ISearch(ar, mid+1, last, target);
}
}이렇게 구현된다. 뭐 솔직히 mid값을 따로 식에 의해 정해준다는 것 말고는 이진탐색과 큰 차이가 없어서, 딱히 뭐가 없다.
물론, 약간의 차이는 있다. 방금 말한 변수 mid 선언과, 탐색 대상이 존재하지 않을때의 if 조건문에서 차이가 있다.
이 if 조건문은, 주석을 그대로 받아들이면 된다. 탐색 범위 안에 탐색 대상이 없으면, 탐색 범위 밖에 있다는 거니까, 계속 탐색을 진행해봤자 의미가 없지않나. 그래서 저렇게 된다.
11-2
이진 탐색 트리
이름만 딱 봐도, 그냥 이진 트리의 일종이다. 이진 "탐색" 트리. 그런데 트리의 구조를 보면, 꽤나 탐색에 효율적이다. 데이터 추가 or 삭제할 때의 성능 평가를 했을 때도 꽤나 효율적인 편이였다. 만약 데이터가 999,999,999가 어딨냐 찾는다 해도, 트리 높이는 30이 안넘는다. (2에 30승이 대충 10억 얼마다)
그런데, 그냥 이진 트리를 그대로 써먹기엔 좀 애매하다. 높이가 적다고 해도, 어떤 길을 갈지 경우의 수가 무지하게 많아지는데, 우리가 찾는 데이터로 커서를 넘긴다고 쳤을 때, 이 커서가 갈 길을 잘 선택해야 한다.
아까 우리가 처음 이 복습내용을 진행할 때, 내가 이런 말을 했다.
"효율적으로 탐색하기 위해, 처음부터 어떻게 저장을 해야할까?"도 고민해줘야한다.
그래서, 이 이진 탐색 트리도 어떻게 저장해야할지도 생각해줘야 한다. 그리고 역시나, 이 이진 탐색 트리도 데이터를 저장하는 규칙이 있다.
즉
이진 트리 + 데이터의 저장 규칙 = 이진 탐색 트리
라고 생각해줘도, 어느정도는 무방하다.
이 "데이터의 저장 규칙" 은, 아래와 같다.
- 이진 탐색 트리의 노드에 저장된 key는 유일하다.
- 루트 노드의 키가 왼쪽 서브 트리를 구성하는 "어떤 노드의 키보다" 크다.
- 루트 노드의 키가 오른쪽 서브 트리를 구성하는 "어떤 노드의 키보다" 작다.
- 왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.
위의 조건에 완전히 부합하는 예시 하나를 보여주겠다.
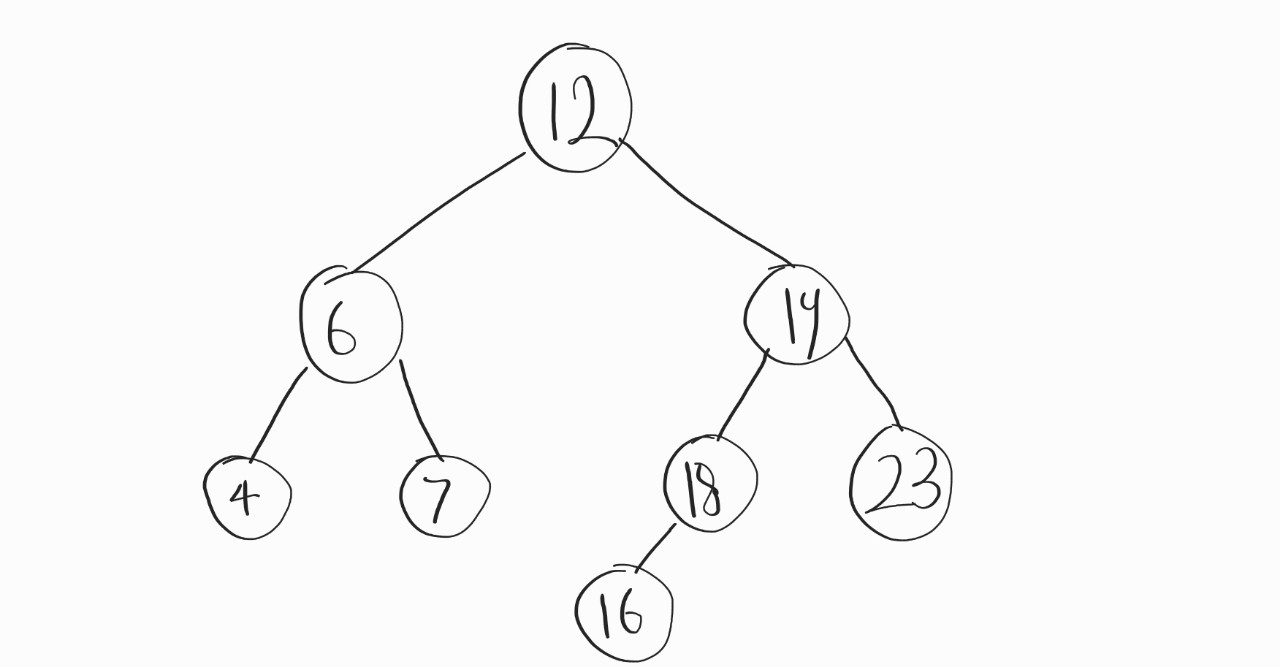
정말 대충 그린 것 같지만, 그러려니 하자
이 예시를 쉽게 표현하면
"왼쪽 자식 노드의 키 < 부모 노드의 키 < 오른쪽 자식 노드의 키"
라는 식이 만족하게 된다.
보면 루트노드의 왼쪽 서브 트리에 저장된 값은 전부 다 12보단 작고, 오른쪽 서브 트리에 저장된 값을 전부 다 12보단 크다.
구현
"이진 (탐색) 트리" 이니 만큼, 이진 트리에서 정의한 기능(ADT)들을 여기서 활용하지 않을 이유가 없다. Ch 08-2 의 BTree.h 파일을 활용하도록 하겠다.
/* BSTree.h */
#ifndef __B_S_TREE_H__
#define __B_S_TREE_H__
#include "BTree.h"
typedef BTData BSTData;
// 이진 탐색 트리 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot);
// 노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode * bst);
// 이진 탐색 트리에 데이터 새로 추가(삽입)
void BSTInsert(BTreeNode **proot, BSTData data);
// target 탐색
BTreeNode *BSTSearch (BTreeNode *bst, BSTData target);
#endif이진 탐색 트리의 헤더파일은 기본적으로 위와 같다.
여기서 본격적인 구현에 앞서, BSTInsert를 구현함에 있어 알아둬야 할게 있다.
바로 이 Insert의 진행 순서인데, 아래와 같다.
- 삽입하는 숫자를 A라고 가정.
- A를 루트노드부터 시작하여 점차 아래쪽으로 비교를 진행해나간다.
- 비교대상보다 값이 작으면 왼쪽 자식노드로 이동, 값이 크면 오른쪽 자식노드로 이동한다.
- 비교 대상이 없을 때 까지 내려간다. 비교 대상이 없는 그 위치가, 새 데이터가 저장될 위치다.
이를 바탕으로, BSTInsert부터 구현해보자.
void BSTInsert(BTreeNode ** pRoot, BSTData data) {
BTreeNode *pNode = NULL; // Parent node
BTreeNode *cNode = *pRoot; // Current node
BTreeNode *nNode = NULL; // New node
while (cnode != NULL) {
if (data == GetData(cNode)) {
return;
} // 데이터 중복 비허용
pNode = cNode;
if (data < GetData(cNode)) {
// 만약 현재 노드보다 새 노드의 data 값이 작다면
cNode = GetLeftSubTree(cNode);
} else {
cNode = GetRightSubTree(cNode);
}
}
// 새로이 추가될 data를 가진 노드 생성
nNode = MakeBTreeNode();
SetData(nNode, data);
if (pNode != NULL) { // 새 노드가 루트노드가 아니면
if (data < GetData(pNode)) {
MakeLeftSubTree(pNode, nNode);
} else {
MakeRightSubTree(pNode, nNode);
}
} else { // 새 노드가 루트노드면
*pRoot = nNode;
}
}그리고, BSTSearch 함수다.
BTreeNode * BSTSearch(BTreeNode *bst, BSTData target) {
BTreeNode *cNode = bst; // 현재 노드
BSTData cd; // 현재 노드의 데이터 cd
while (cNode != NULL) {
cd = GetData(cNode);
if (target == cd) return cNode;
else if (target < cd) cNode = GetLeftSubTree(cNode);
else cNode = GetRightSubTree(cNode);
}
// while문을 빠져나왔다면, 탐색대상이 저장되어있지 않을 때다.
return NULL;
}일단, 여기까지.
나머지 이진 탐색 트리의 기능인 삭제는 이후에 따로 적겠다.