[Aiffel] 아이펠 33일차 개념 정리 및 회고

1. 딥러닝 개념 정리

1) 퍼셉트론

• 레이어를 이루고 있는 각각의 노드를 퍼셉트론이라고 칭함

신경세포	퍼셉트론
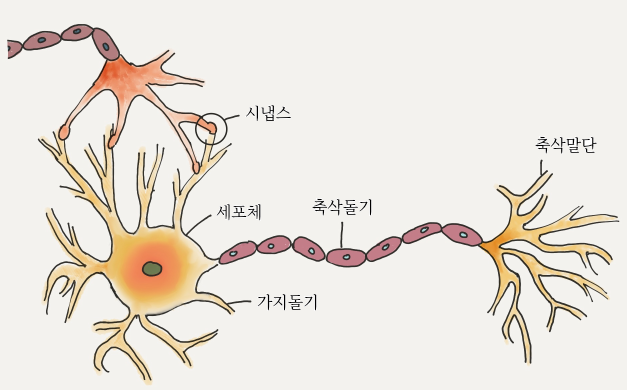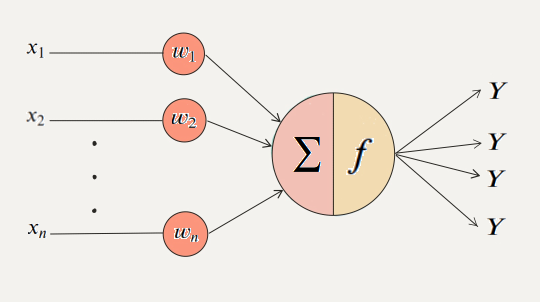가지돌기	입력 신호
축삭돌기	출력 신호
시냅스	가중치
세포 활성화	활성화 함수

2) 활성화 함수

(1) 기본 정리

1. 의미

• 어떤 조건을 만족시킨 여부와 관련
  • 특정 조건을 만족시킬 경우 '활성화'시킴

2. 사용 이유
   딥러닝 모델의 표현력(representation capacity, expressivity)을 향상시키기 위함

   선형함수로는 비선형 함수를 표현할 수 없다.
   하지만 딥러닝 모델에서 parameter와 입력값 x는 선형관계를 띈다. 가중치를 곱해 bias를 더하는 방식이기 때문이다. 따라서 비선형 데이터(이미지, 동영상 등 복잡한 형태를 띄는 데이터)를 학습해 표현하기 위해선 딥러닝 모델 또한 비선형성을 띄어야 한다. 이러한 비선형성을 부여하기 위한 함수가 활성화 함수인 것이다. 활성화 함수를 레이어 사이에 배치함으로써 모델이 비선형 데이터를 표현할 수 있도록 한다.

3. 역할

• 세포체가 하는 역할과 비슷: 입력된 신호가 특정 임계점을 넘으면 출력, 그렇지 않을 경우 무시

선형변환의 정의
V, W는 벡터공간이며 모두(같은 체(field)에 있다고 표현해야하나, 지금은 실수만 다루기 때문에 이렇게 가정) 실수 집합 상에 있다(V를 이루는 원소들이 실수)고 가정할 때,

$T:V→W$

는 다음 두 가지 조건을 만족한다고 하자.
1. 가산성(additivity)

$x, y \in Vx,y∈V 에 대해, \mathcal{T}(x+y) = \mathcal{T}(x)+ \mathcal{T}(y)T(x+y)=T(x)+T(y)$

2. 동차성(Homogeneity)
   $모든 x \in V, c \in \Bbb{R}x∈V,c∈R 에 대해, \mathcal{T}(cx) = c\mathcal{T}(x)T(cx)=cT(x)$

4. 비선형 활성화 함수를 사용하는 이유

• 선형 함수를 활용할 경우 노드를 아무리 늘려도 하나의 노드를 사용하는 것과 다름이 없음.
  • 비선형적 특성을 가진 데이터를 예측 불가

(2) 활성화 함수의 종류

1. 이진 계단 함수
   

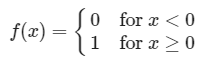
• 단층 퍼셉트론(초기 신경망)에 자주 사용됨
• 한계
  • XOR 문제 해결 불가 ⇒ 다층 퍼셉트론으로 해결
  • 역전파 알고리즘 사용 불가: 0에서 미분 불가능, 다른 수에선 미분하면 0만 나와서 가중치 업데이트 안됨
  • 다중 출력 불가

2. 선형 활성화 함수

• 다중 출력 가능: 간단한 다중 분류 문제 해결 가능
• 미분 가능: 역전파 알고리즘 적용 가능
• 한계: 비선형 데이터 예측 불가

3. 비선형 활성화 함수

• 시그모이드(=logistic activation function)
• softmax: 마지막 layer에서 여러 항목 별로 분류하기 위해 사용. 여기서 다루는 내용은 hidden layer에서 쓰이는 활성화 함수에 관한 것이므로 자세한 내용은 다루지 않음

2. CS231n 6강 정리

참고
cs231n 6강 Training Neural Network 1 정리

1) 활성화 함수

활성화 함수	공식	좌표	한계	해결
sigmoid		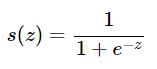	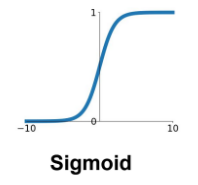1. vanishing gradient 2. zero-center 3. exp 연산에서 비용이 많이 듦
tanh		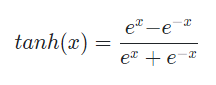	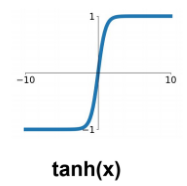1. vanishing gradient
ReLu			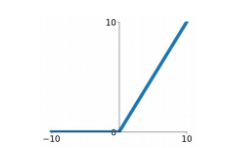1. zero-centered output 2. 음수에서 vanishing gradient	1. vanishing gradient 부분 해결: 양의 방향에서 입력값 x를 그대로 배출함으로써 기울기 유지 2. 연산 효율 향상: exp 계산 없음
Leaky ReLu		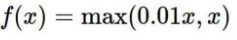		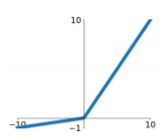1. vanishing gradient 문제 보완
PReLu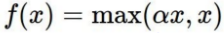
ELU		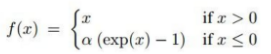	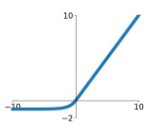1. 음의 영역에서 기울기 소실 2.exp 연산으로 비용이 커짐	0에서 미분 불가능했던 점을 보완한 함수

(1) sigmoid 함수

1. vanishing gradient

• 0 또는 1에서 포화됨
  • 입력값이 아무리 커져도 함수 값이 1에 수렴할 뿐 1보다 커지지 않음, 반대의 경우 0에 수렴
    • gradient가 0에 수렴 ⇒ 역전파에서 문제
• backpropagation에서의 문제
  • w = local gradient * global gradient
    • 여기서 global gradient는 이전 노드의 기울기인데, 이 값이 0에 수렴하니 가중치 w의 값도 결국 0에 수렴하게 됨.
    • w 업데이트 불가 (= kill the gradient)

2. non zero-centered: 훈련이 비효율적으로 이루어져(zigzag 현상) 시간이 오래 걸림
   

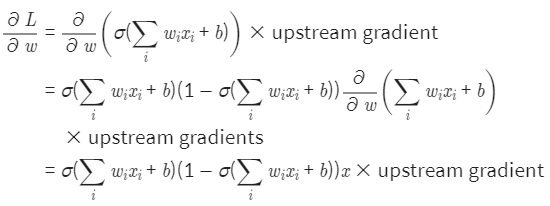
• 첫 줄: 가중치에 대한 미분, 합성함수 미분이므로 겉에 있는 시그모이드 함수를 미분하고 안에 있는 가중치의 합을 나타내는 값을 미분해서 곱한다.
• 둘째 줄: 시그모이드 함수는 미분하면 σ(x)(1−σ(x)) 이므로
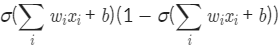
  바로 다음에 곱한 식은
  
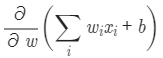
  합성함수에서 가장 안쪽의 함수를 미분한 것에 해당(첫 줄에서 설명한 가중치의 합을 나타내는 값을 미분하는 것)
• 세 번째 줄: 가중치 w에 대해서 미분했을 때 일차함수인 가중치의 합의 경우 x만 남는다.

마지막 식을 보면 upstream gradient(=global gradient) 외의 값은 모두 양수이다. 따라서 $\frac{\partial L}{\partial w}$의 값은 upstream gradient의 부호에 의해서 결정된다. (다른 풀이 방식은 아래 사진 참고)

upstream gradient의 부호에 따라 노드의 가중치는 모두 양의 방향으로 업데이트 되거나 음의 방향으로 업데이트 될 것. = 지그재그 모양을 띄면서 업데이트 하게 됨 = 비효율적

• output 값이 항상 양수: 양수의 값만 input으로 사용될 것
  
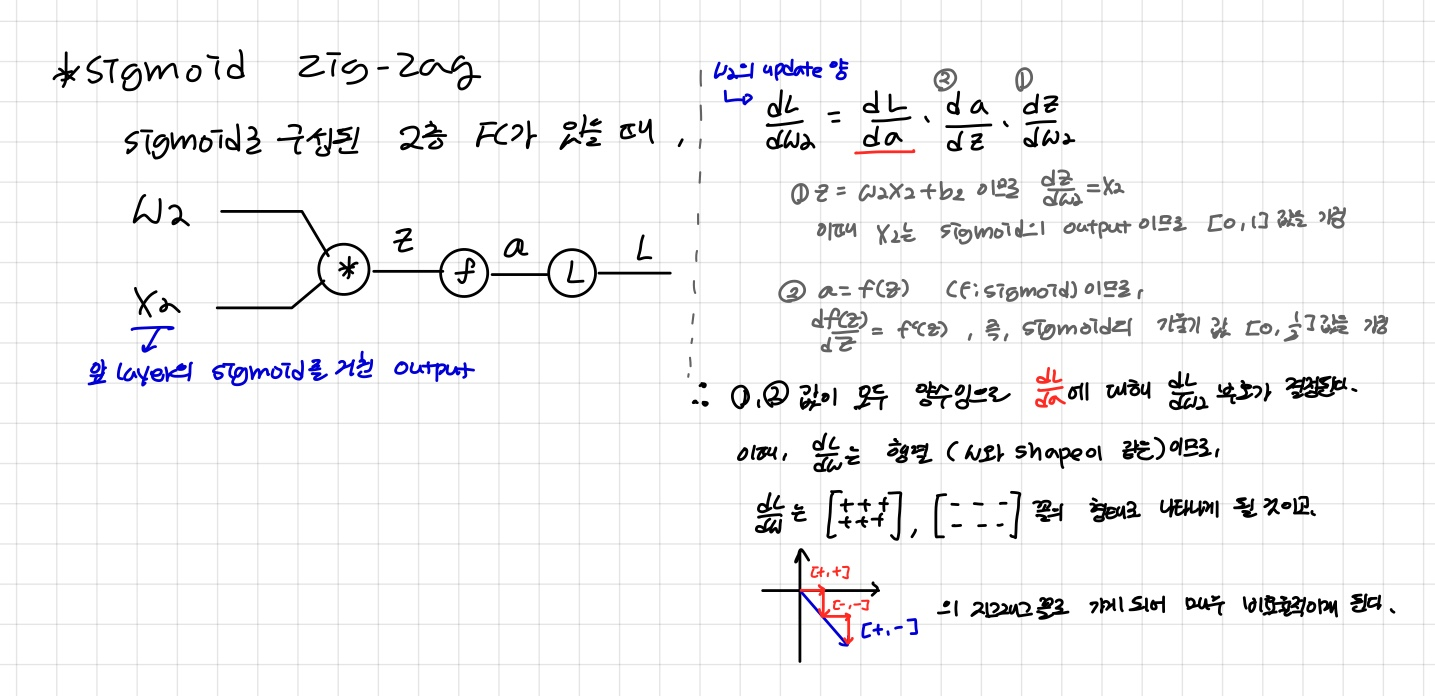
  모두 양수가 되는 경우
  • 시그모이드의 기울기, output값이 모두 양수이기 때문에 가장 앞에 있는 $\frac{\partial L}{\partial w}$에 의해 부호가 결정됨.
  • 따라서 w2의 업데이트 양에 해당하는 $\frac{\partial L}{\partial w2}$는 결국 모두 양, 혹은 음이기 때문에 지그재그를 그리는 형태를 띄게 된다. 이는 매우 비효율적인 방식이다.

위와 같은 문제로 인해서 시그모이드 함수는 보통 쓰지 활성화 함수로 쓰지 않음. 마지막에 결과값을 반환하는 데에 이용함.

(2) tanh

1. zero centered output 문제는 해결
2. vanishing problem 해결 못함: -1 또는 1에서 포화되기 때문

(3) ReLu

1. 음의 영역에서 시그모이드와 같은 문제가 나타남
   
   ex) dead ReLu: 입력값이 -10, 0일 때 gradien가 0, 즉 기울기가 소실된 상태에 빠진다
   • 가중치 초기화에서 dead ReLu가 되어버리면 업데이트가 안될 수 있음
   • learning rate를 크게 설정할 경우 자주 발생. 이러한 경우 w가 크게 비약해 학습이 안될 수 있음
   • 제시된 해결법: 약간의 bias 부여 (시도를 하는 경우도 있고 안하는 경우도 있음)
2. non zero-centered

(4) Leaky ReLu

1. vanishing gradient 해결
   음수 부분에서 경미한 기울기를 부여해 기울기 소실 문제를 해결함

2) Preprocess the data: 데이터 전처리

1. zero-centering & normalize
   : 이미지 데이터에서는 픽셀의 범위가 0~255로 동일하기 때문에 zero-centering 만 수행함
   zero centering을 하면 지그재그 현상(가중치가 전부 음수 혹은 양수가 되어서 업데이트가 일방향으로, 비효율적으로 진행되는 현상)을 피할 수 있기 때문. 따라서 zero-mean으로 전처리
   하지만 이는 첫 번째 레이어에만 효과가 있음. 이후 네트워크가 깊어질 수록 활성화 함수에 의해 처리되는 값이 양수만 나오기 때문

2. PCA & Whitening
   이미지 데이터에선 수행하지 않음: 공간적 구조를 기반으로 이미지를 다루기 때문

3) Weight initialization

1. what happens when W=0 init is used?

• 전부 죽어서 학습 안됨: 일부 정답
• 뉴런이 모두 죽는 것이 아니라 똑같은 수행을 하게 됨 ⇒ layer가 소용 없음, gradient의 업데이트도 일어나지 않음

2. 첫 번째 아이디어: small random numbers - 가장 첫 번째 가중치에 작은 랜덤 값을 부여

• 강의 예시: tanh을 활용할 경우
  • layer가 깊어질 수록 편차가 사라져 모든 값이 0에 수렴하는 현상이 일어남
  • 1보다 작은 값을 이용해 가중치를 랜덤하게 설정하다보니 곱할 수록 0에 수렴하게 되는 것
  • gradient의 업데이트도 잘 이뤄지지 않음
  • 가중치에 1을 곱해 0에 수렴하지 않게 하는 경우?
    • explode하게 됨

3. Xavier initialization의 방식

• tanh을 활용할 때, 랜덤한 가우시안 분포 값에서 np.sqrt(fan_in)으로 나눠 스케일링함. 상대적으로 값을 조절하며 초기화 가능하기 때문에 위의 두 방식보다 합리적
• ReLu는 zero-mean이 아니기 때문에 이 방식을 사용하면 음수인 경우 문제가 발생함.
  • 뉴런의 절반이 죽는다는 점에서 착안해 2를 나눈 np.sqrt(fan_in/2)를 활용함. 이렇게 하면 결과가 나아짐

4) Batch Normalization

1. 가우시안 범위 내에서 activation 값을 뽑고자 하는 아이디어에서 기인함
   현재 batch에서의 평균, 분산을 활용해 훈련의 처음부터 batch normalization을 취하여 모든 층이 정규분포를 따르도록 하는 방식

2. 사용

• ConV 층과 FC층 후, 활성화 함수를 거치기 전에 batch norm을 넣어줌
  • 두 레이어의 차이: activation map에서의 spatial location 정보가 중요한 ConV 층에서는 activation map 당 한 개의 평균과 표준편차를 사용해 normalization을 수행
• 이런 식으로 normalization을 진행할 경우, tanh을 예로 들면 tanh에서 linear한 부분으로 범위를 강제할 수 있음. 즉, saturate 되는 경우를 어느 정도 통제하는 것.
• 본래 값으로 변경하고 싶을 땐 감마를 곱한 후(scaling) 베타를 더한다(shifting).
• regulation 효과도 있음
• 선형 변환이기 때문에 공간은 변하지 않음

5) Babysitting the Learning Process

network architecture을 구성하는 방법, 학습 과정을 보는 방법, 하이퍼 파라미터 조정 방법
1. 데이터 전처리
2. architecture 구성
3. loss 함수 지정 or regularization
4. Sanity check (train set에서 일부만 활용)

• 이때 overfitting이 나오면 제대로 동작하고 있다는 의미로 생각하면 됨

5. 전체 데이터 학습, loss를 확인하며 learning rate 조정

6) Hyperparameter Optimization

(1) Cross-validation

넓은 범위에서 좁은 범위로 좁혀가며 hyperparameter 조정

(2) Random search vs Grid search

random search가 나음, grid는 일정 간격을 가지고 있기 때문에 best case를 찾지 못할 가능성이 큼
grid의 경우 hyperparameter의 값이 많아질 수록 차원의 수가 늘어나 계산 비용이 크게 든다. 따라서 차원이 4개 이상인 경우엔 random search를 하는 것이 더 효과적임.

3. 회고

이제까지 배운 내용을 정리할 수 있었다. 미적분 내용을 보면서 이해안되는 부분이 있었는데 LMS에서 설명한 부분하고 강의에서 설명한 부분하고 비교하면서 보니 이해가 됐다. 여러 가지 질문에 대해서도 다는 아니더라도 몇 가지 정도는 바로 답을 떠올리고 답할 수 있게 되었다. 완벽하진 않지만 공부가 되어가는 느낌이다.