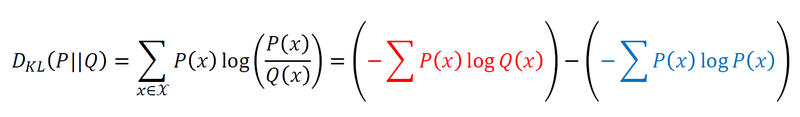1. 정보이론 톺아보기
정보이론이란?
'정보'라는 추상적인 개념을 정량화하며, 정보의 저장과 통신을 연구하는 분야
1) Information Content
- <Deep Learning>(Goodfellow, Bengio, Courville)에서 말하는 정보의 정량성
- 어떤 사건이 일어날 가능성이 높을 경우 정보량은 낮음
- 반드시 일어나는 사건은 정보량이 없는 것과 같음
- 일어날 가능성이 낮은 사건은 정보량이 높음
- 두 가지 독립된 사건이 있을 때, 전체 정보량은 각각의 정보량을 더한 것과 같음
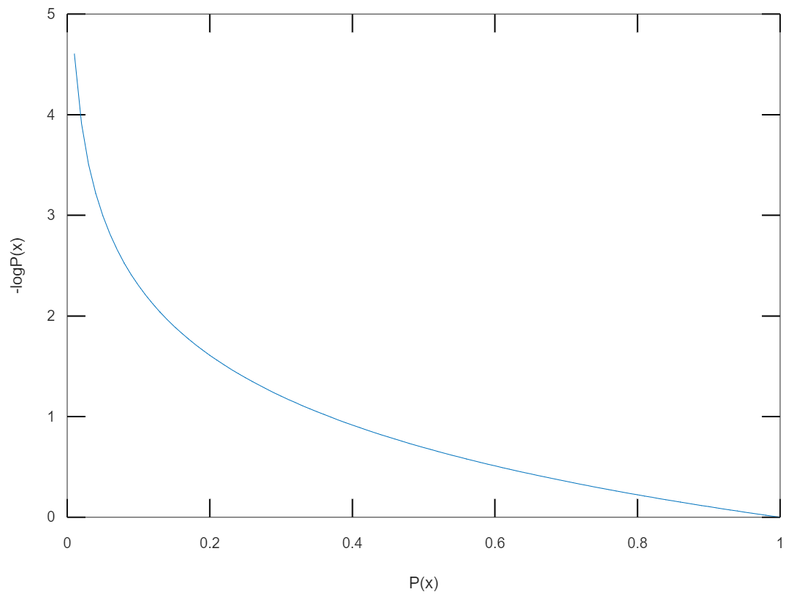
- information content(정보량)과 사건 x가 일어날 확률 의 관계
- 와 의 관계
2) Entropy
-
의미
특정 확률분포를 따르는 사건들의 정보량 기댓값
(확률변수가 가지는 모든 경우의 수에 대한 정보량을 구한 후 평균을 낸 값) -
이산 확률 변수의 경우
여러 색깔의 공이 있다고 가정했을 때
- 엔트로피가 가장 높은 경우 = 공의 색깔이 모두 다른 경우 = 불확실성이 높음
- 엔트로피가 가장 낮을 경우 = 공의 색깔이 모두 같은 경우 = 불확실성이 낮음
- 공의 색깔이 균등할 수록 엔트로피는 증가
균등분포
- 모든 경우의 수 각각의 확률이 같을 때
- 연속 확률 변수(미분 엔트로피, differential entropy)의 경우
적분의 형태로 정의
3) Kullback Leibler Divergence
- 머신러닝 모델 종류
- 결정 모델: 실제 데이터 분포를 모델링하지 않고 결정 경계만 학습
- ex) 0보다 작으면 데이터를 1로 분류, 0보다 크면 2로 분류
- 생성 모델: 데이터의 실제 분포를 간접적으로 모델링하는 방식. 데이터와 모델에서 도출 가능한 여러 확률 분포와 베이즈 이론을 활용함.
- 클백-라이블러 발산
-
생성 모델을 학습시킬 때, 실제 분포와 머신러닝이 나타내는 확률 분포 사이의 차이를 나타내는 지표
-
: 데이터가 따르는 실제 확률 분포
-
: 모델이 나타내는 확률 분포
-
이산 확률 변수인 경우
-
연속 확률 변수인 경우
- 특징
- 거리함수와 비슷한 성질: 두 확률 분포의 차이를 나타내기 때문
- ✔✔✔🤔
- non-symmetric: (거리함수와 다른 점)
머신러닝에서는 두 확률 분포의 차이를 줄이는 방향 = $가 최소가 되는 방향
으로 학습시킴
- 파란색 부분은 고정값이기 때문에 빨간색 값을 조절하는 것 = 빨간색 값을 최소화
- 빨간색은 P(x)에 대한 Q(x)의 교차 엔트로피식
- 파란색은 P(x)에 대한 P(x)의 엔트로피식
- Cross Entropy
P(x)에 대한 Q(x)의 교차 엔트로피 식
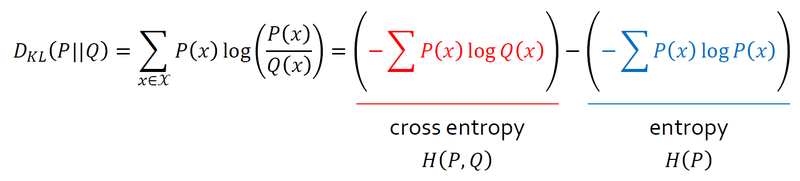
- KL divergence를 최소화하는 것은 곧 교차 엔트로피를 최소화하는 것과 같다.
4) Cross Entropy Loss
- cross entropy: 손실함수의 한 종류
ex) 3개()로 분류하는 문제가 있다고 할 때, 어떤 데이터의 출력값이 다음과 같다고 가정한다.
위의 결과는 곧 다음과 같은 의미이다.
데이터가 실제로 2번 클래스에 속하는 경우, 데이터의 실제 확률 분포는 one-hot encoding과 같은 [0, 1, 0]이다.
cross entropy를 이용하면 다음과 같은 결과가 나온다.
- Likelihood와의 관계
- 모델의 파라미터를 θ로 놓으면 모델이 표현하는 확률분포는 로, 데이터의 실제 분포는 로 표현할 수 있음
- 는 데이터셋, 파라미터가 있을 대 예측값의 분포를 나타냄. 따라서 모델의 likelihood와 같음
X와 는 데이터셋에 의해 결정되기 때문에 모델의 식이 바뀌어도 변하지 않음
따라서 바꿀 수 있는 부분은 이다. 따라서 cross entropy를 최소화하는 파라미터 값을 구하는 것은 결국 negative log likelihood를 최소화하는 파라미터를 구하는 것과 같다.
5) Decision Tree와 Entropy
- 의사결정 트리
- 보유한 데이터에서 특정 기준으로 전체 데이터를 나눴을 때, 나누기 이전과 비교해 엔트로피의 감소 여부를 따진다. 이때 엔트로피가 감소하면 그만큼 모델 내부에서 정보 이득을 얻었다고 보는 관점.
- 엔트로피의 증가가 정보 손실량이라고 정의하는 것과 반대되는 관점
- : 전체 사건의 집합
- : 분류 기준이 될 수 있는 속성(feature)의 집합
- : 는 에 속하는 속성(ex 가 Outlook일 때 는 Sunny)
- : 속성을 가진 의 부분 집합
- : 집합 X의 크기(원소의 개수)
- : X라는 사건 집합이 지닌 엔트로피
- 는 분류 기준을 채택함으로써 정보 이득의 양을 의미함
- 의사결정 트리에서의 entropy
- 깊이를 지정하는 것이 overfitting을 막을 수 있음
- Random Forest: Decision Tree를 앙상블함. DT의 단점 보완
2. 회고
수식이 많이 나왔지만 다른 날보단 이해가 잘 됐다. 그래도 기본적인 통계공부가 필요함을 느낀다.