[DL] Transformer

*해당 포스팅은 <딥 러닝을 이용한 자연어 처리 입문>을 참고하여 정리했습니다. 항상 원문이 더 뛰어납니다.

Attention 모델이 장기의존성 문제를 해결했지만, 아직 남은 문제가 있습니다. 병렬처리 문제입니다. attention 모델도 결국 time-step마다 input되는 값을 처리하는 모델이기 때문에 데이터를 순차적으로 처리할 수 밖에 없습니다. 이번에 정리할 transformer는 이러한 문제를 해결하기 위해 등장한 모델입니다.

transformer 모델은 모든 토큰을 동시에 입력받아 병렬 처리하기 때문에 GPU 연산에 최적화되어 있습니다.

1. Transformer의 구조

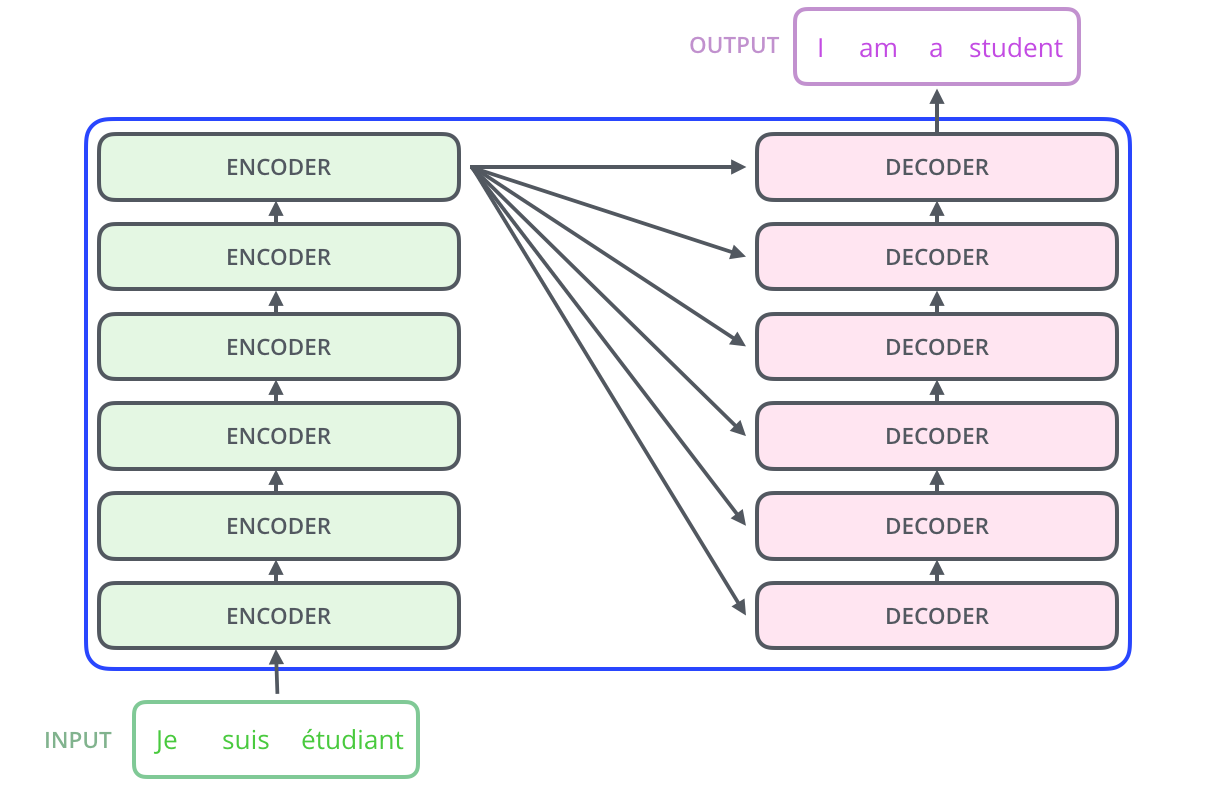
transformer의 구조를 시각화한 이미지입니다. transformer는 attention 모델처럼 인코더에서 입력 시퀀스를 입력받고, 디코더에서 출력 시퀀스를 출력하는 인코더-디코더 구조입니다. 대신 attention 모델이 각 time-step마다 하나의 메모리 셀(인코더)를 가지고 있었다면, transformer는 n개의 셀(인코더)를 가질 수 있습니다. 위 이미지는 인코더와 디코더를 각각 6개 사용하고 있습니다.

이제 이 구조 안에서 입력 시퀀스가 어떻게 처리되는지 자세히 살펴보도록 하겠습니다.

2. Transformer 인코더 연산 과정

입력 과정부터 하나씩 살펴보겠습니다.

1) Positional Encoding

Transformer는 병렬화를 위해 모든 단어 벡터를 동시에 입력받습니다. 시퀀스의 모든 토큰이 동시에 입력되기 때문에 어떤 단어가 어디에 위치하는지 컴퓨터는 알 수 없습니다. 그렇기 때문에 순서 정보를 전달하기 위해 순서 정보를 담은 벡터를 단어 토큰의 임베딩 벡터와 함께 전달해야 합니다. 단어의 상대적인 위치 정보를 담은 벡터를 만드는 과정을 Positional Encoding이라고 합니다.

임베딩 벡터가 Positional Encoding과 더해지는 과정을 시각화한 이미지입니다. transformer는 위치 정보를 가진 값을 만들기 위해 아래 수식을 사용합니다.

다소 복잡한 수식이지만, 사인 함수와 코사인 함수의 파동 형태의 그래프를 떠올려보면 positional encoding이 작동하는 방식에 대해 힌트를 얻을 수 있습니다. 이 파동 형태의 값이 임베딩 벡터에 더해지기 때문에 순서 정보가 생기는 것입니다. 임베딩 벡터 내의 각 차원의 인덱스가 짝수인 경우에는 sin 함수를, 홀수인 경우에는 cos 함수를 사용합니다. 중요한 것은 이 과정이 행렬 단위로 이루어진다는 것입니다. 임베딩 벡터와 positional encoding의 덧셈은 임베딩 벡터가 모여 만들어진 문장 행렬과 positional 행렬의 덧셈 연산을 통해 이루어집니다.

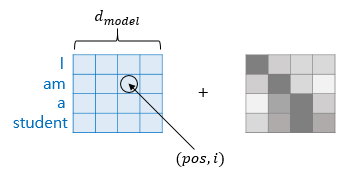
위 이미지로 행렬 단위로 연산이 이루어지는 과정을 확인하실 수 있습니다.

2) Self-Attention

Position-encoding을 통해 순서정보를 갖게 된 임베딩 벡터는 인코더에서 Self-Attention 연산을 거칩니다. Transformer에서는 총 세번의 Attention을 거치게 됩니다. Self-Attention은 인코더에서 진행되는 첫 번째 Attention입니다.

인코딩의 attention이 Self-Attention인 이유는 Query, Key, Value의 출처가 같기 때문입니다. 시퀀스 행렬에 각각 Query, Key, Value 가중치 행렬을 내적하여 Query, Key, Value 벡터(행렬)을 만들어냅니다. 즉, 이 세 값의 출처는 모두 input된 시퀀스 행렬입니다. 각각의 벡터는 아래와 같은 역할을 합니다.

• 쿼리(q)는 분석하고자 하는 단어에 대한 가중치 벡터입니다.
• 키(k)는 각 단어가 쿼리에 해당하는 단어와 얼마나 연관있는 지를 비교하기 위한 가중치 벡터입니다.
• 밸류(v)는 각 단어의 의미를 살려주기 위한 가중치 벡터입니다.

The animal didn't cross the street because it was too tired

위 문장으로 쿼리, 키, 밸류가 어떻게 동작하는지 보겠습니다. 위 문장을 제대로 번역하려면 It이 무엇을 의미하는지 알아야 합니다. 컴퓨터는 It이 animal을 뜻하는지, street을 뜻하는지 알길이 없습니다. 이때 쿼리-키-밸류 연산으로 It과 가까운 단어를 찾아줍니다. 아래 이미지를 보겠습니다. 'It'이 어떤 단어와 가장 연관되어 있는지를 시각화한 그림입니다.

쿼리, 키, 밸류로 연관 관계를 찾는 연산과정입니다. attention 매커니즘과 동일합니다.

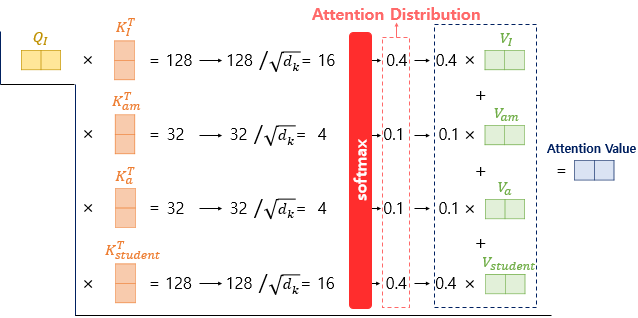
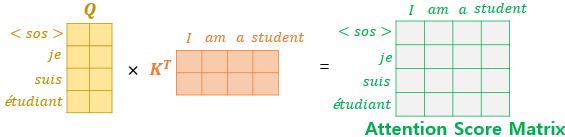
1. 특정 단어의 쿼리 벡터와 모든 단어의 키 벡터를 내적합니다. 내적의 결과를 Attention Score라고 합니다.
2. Attention Score를 쿼리, 키, 밸류 벡터의 차원인 $d_k$의 제곱근으로 나눠줍니다. 만약 임베딩 벡터의 차원이 512이고, 시퀀스를 병렬로 처리하기 위해 분할된 head가 8이라면, $d_k$는 64(512/8)입니다. $d_k$의 제곱근으로 Attention Score를 나누어 계산값을 안정적으로 만들어주는 보정을 합니다.
3. Attention Score에 소프트맥스 함수를 취해서 Attention distribution을 구합니다. 그리고 각 Attention Weight에 밸류를 가중합하여 최종적으로 Attention Value를 구합니다.
4. 위 과정은 벡터 차원에서 이뤄지는 것이 아니라 행렬 단위로 이루어집니다. 즉 병렬 계산입니다. 아래는 이 과정을 한 눈에 볼 수 있도록 정리된 이미지입니다.

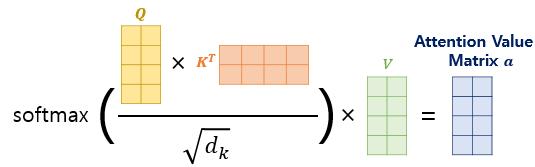
3) Multi-Head Attention

위와 같은 Self-Attention은 한 번에 이뤄지지 않습니다. 이게 무슨 말인가 하면, 임베딩 벡터가 512 차원이고, 시퀀스의 길이가 20인 데이터는 20 512 차원의 시퀀스 행렬이 됩니다. Transformer는 20 512 차원의 시퀀스를 한 번에 계산하지 않습니다. 차원을 여러개로 나누어 Attention을 수행합니다. num_head가 8이라면 시퀀스 행렬은 20 * 64로 변하여 각각 Attention이 수행된 다음에 마지막에 출력되는 각각의 Attention Value를 Attention Head라고 합니다. 8개의 Attention Head는 Concatenate되어 하나의 행렬로 출력됩니다.

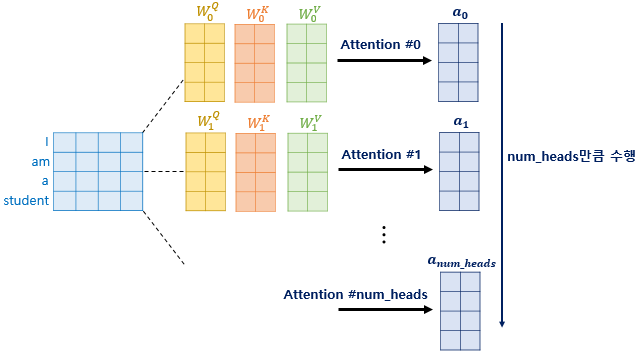
이때 시퀀스 행렬과 내적되는 가중치 행렬의 값은 모두 다릅니다. 여기서 병렬 Attention의 효과가 발생합니다. 각각 다른 가중치로 시퀀스 행렬을 내적함으로써 쿼리 벡터를 다양한 각도에서 바라볼 수 있게 합니다. 첫 번째 Attention Head가 It과 Animal의 연관도를 높게 봤다면, 두 번째 Attention Head는 It과 tired의 연관도를 높게 볼 수 있습니다. 각 Attention Head가 Query를 다양한 각도에서 바라봄으로써 Query와 Key의 관계 간에 빈틈이 없어지는 것입니다.

4) Layer Normalization & Skip Connection

Multi-Head Attention에서 출력된 벡터는 Layer normalization과 skip connection을 거칩니다. 인코더, 디코더에 내장되어 있는 서브 레이어에서 출력된 모든 벡터는 Layer normalization과 skip connection을 거치게 됩니다. Layer normalization의 효과는 Batch normalization과 유사합니다. 출력된 벡터를 정규화하여 더 빠르고 안정적으로 학습할 수 있도록 합니다.

skip connection은 역전파 과정에서 정보가 소실되지 않도록 하는 역할을 합니다. 활성 함수를 거치지 않은 x를 f(x)에 더함으로써 역전파 과정에서도 1 이상의 값을 보존할 수 있도록 합니다. 이렇게 하면 층이 깊어짐에 따라 발생하는 기울기 소실 문제를 어느정도 해결할 수 있습니다.

5) Feed Forward Neural Network

정규화된 출력값은 FFNN 층으로 들어갑니다. 아직 디코더를 설명하지 않았지만 디코더에도 FFNN층이 있습니다. 첫 번째 가중치 행렬을 지날 때 FFNN 층에 들어갔던 Attention value의 차원이 늘어납니다. 차원이 늘어난 상태로 ReLu 함수를 통과한 뒤 두 번째 가중치 행렬과 곱해짐으로써 원래의 차원으로 돌아옵니다.

3. Transformer 디코더 연산 과정

여기까지가 인코더 내에서 이뤄지는 연산입니다. 이제 디코더로 넘어가보겠습니다. 앞서 6개의 인코더 층이 있다고 가정했는데요. Attention 연산을 순차적으로 마친 마지막 6번째 출력값을 디코더에 전달하게 됩니다.

1) Masked Self-Attention

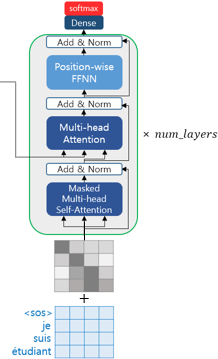
위 그림에서 보듯이 디코더도 인코더와 동일하게 Positional Encoding을 거친 후 문장 행렬이 입력됩니다. 다른 점은 t시점의 단어보다 뒤에 있는 t+1, t+2의 단어들을 마스킹한다는 점입니다.

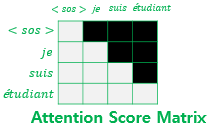
RNN과 같은 seq2seq 모델은 단어가 순차적으로 입력됩니다. 그래서 신경망은 다음 단어를 예측할 때 이전 시점에 입력된 단어들만 참고할 수 있습니다. 하지만 Transformer는 모든 단어가 병렬로 입력됩니다. 현재 시점의 단어를 예측할 때 미래 시점의 단어도 참고할 수 있는 누수가 일어나게 되는 것입니다. 이러한 누수를 막기 위해 디코더의 Self-Attention은 미래 시점의 단어가 마스킹된 시퀀스 행렬을 사용해야 합니다..

마스킹이 적용되는 과정은 다음과 같습니다.

1. 디코더의 첫 번째 서브층인 Multi-Head (self) Attention에서 인코더의 Attention과 같은 연산을 진행합니다. 쿼리 행렬과 키 행렬을 내적하고, 내적한 행렬(Attention Score)를 행렬 차원의 제곱근으로 나눕니다.
2. 보정된 Attention Score에 소프트맥스 함수를 적용하기 전에 가려주고자 하는 요소에만 $-\infty$에 해당하는 매우 작은 수를 더합니다.

3. 마스킹된 값은 Softmax를 취했을 때 0이 나오게 되므로 Value 계산에 반영되지 않습니다.

2) Encoder-Decoder Attention

이제 디코더의 두 번째 Attention입니다. 디코더에서 Masked Self-Attention 층을 지난 벡터는 Encoder-Decoder Attention 층으로 입력됩니다. 이 층에서는 self-Attention이 일어나지 않습니다. Encoder-Decoder attention은 Query는 Decoder 행렬이고, Key와 Value는 인코더 행렬입니다.

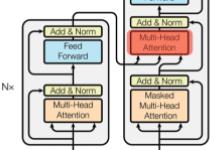
번역을 예로 들자면, 이 층에서는 번역할 문장과 번역된 문장 간의 연관성을 연산하는 것입니다. 번역할 문장과 번역되는 문장의 정보 관계를 엮어주는 부분입니다. 쿼리 행렬(벡터)는 Decoder의 Masked Self-Attention에서 출력된 벡터를 사용하고, 키와 밸류 행렬(벡터)는 인코더의 가장 마지막 블록에서 사용했던 값을 그대로 사용합니다.

쿼리, 키, 벨류 행렬을 가져온 뒤의 연산 과정은 Self-Attention 과정과 동일합니다.

3) Linear & Softmax Layer

Transformer 모델의 마지막 부분입니다. Decoder의 FFNN 층까지 통과한 벡터는 Linear 층을 지나 Softmax를 통해 예측할 단어의 확률을 구하고, 확률에 따라 단어 혹은 시퀀스를 리턴합니다.

4. 정리

Transformer는 인코더에서 시퀀스 안에서 단어들 간의 연관성을 구하고(Self Attention), 디코더에서는 input data와 target data 간의 연관성을 구해서(Encoder-Decoder Attendtion) 예측의 정확도를 높입니다. 그 과정에서 순서 정보를 부여하기 위해 Positional Encoding을 하고, 데이터의 누수를 막기 위해 Masking을 하는 등의 과정이 있지만, Transformer 모델의 핵심은 행렬 단위로 처리되는 Self Attention과 Encoder-Decoder Attention입니다.