
딥러닝에 관한 첫 포스팅입니다. 딥러닝에 사용하는 모델 중 가장 기본적인 피드 포워드 신경망으로 인공신경망의 기본 구조에 대해 정리하도록 하겠습니다.
1. 퍼셉트론
퍼셉트론은 인공 신경망을 이루는 가장 기본 단위입니다. 노드라고도 부르는 이 퍼셉트론은 인간의 세포에서 뉴런과 비슷한 역할을 합니다. 인간의 뉴런은 외부로부터 자극을 받아서 해당 자극에 대해 반응을 할지(1), 혹은 반응하지 않을지(0)를 결정합니다. 반응을 하기로 결정했다면 다음 뉴런에 자극을 전달하고, 자극은 받은 신체 기관은 자극에 대한 적절한 반응을 보입니다. 만약에 처음 보는 자극이라면 학습이 필요하겠죠.
인공신경망의 퍼셉트론도 뉴런과 비슷한 알고리즘으로 움직입니다. 인공신경망 모델은 신호(이미지, 숫자, 영상 등)를 받아서 적절한 Target 값을 도출하는 학습하는 지도 학습 알고리즘입니다. 그리고 그 신호를 Target까지 전달하는 역할을 퍼셉트론이 수행합니다.
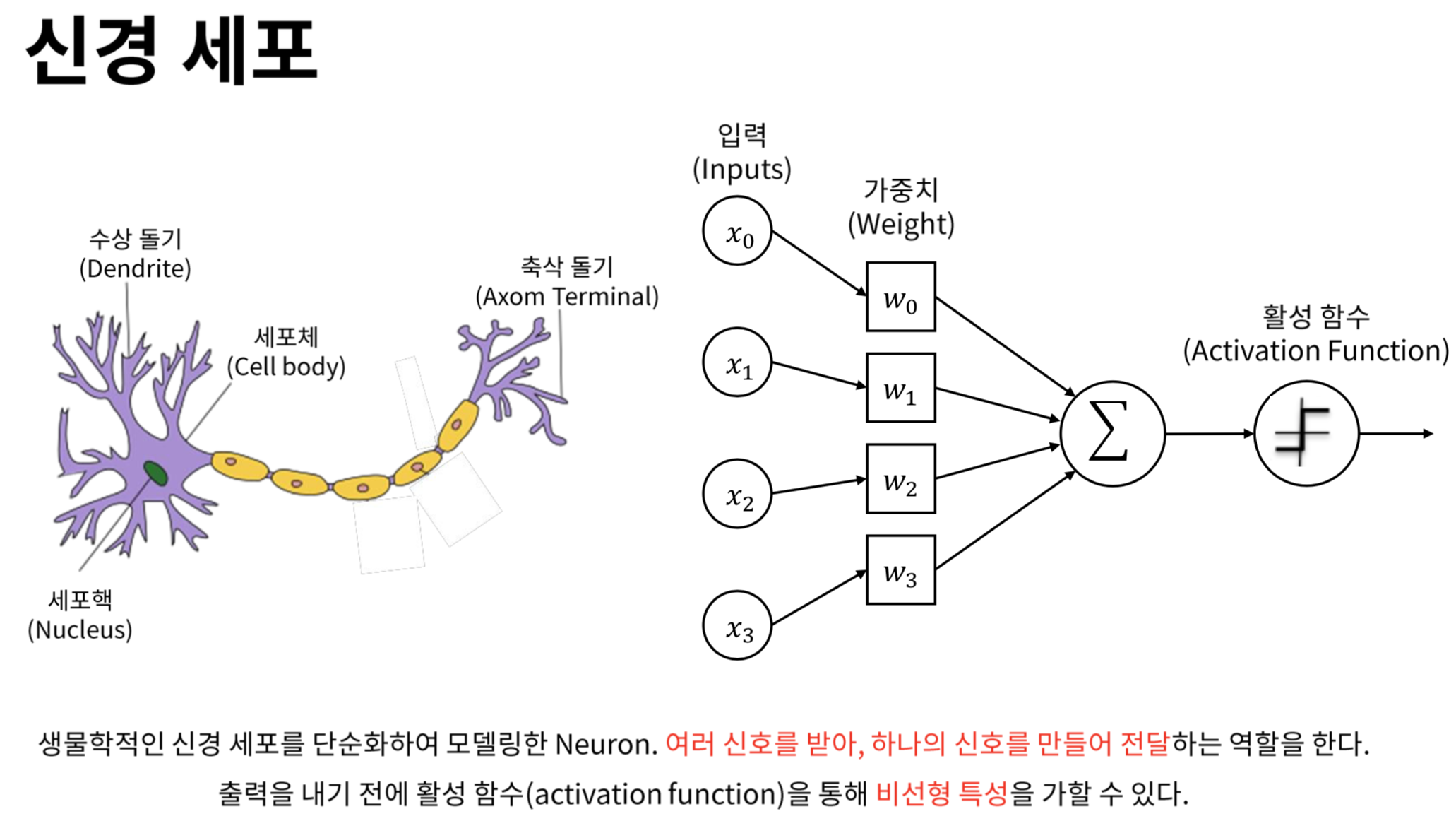
간단히 정리해보겠습니다.
- 퍼셉트론은 인공 신경망을 이루는 가장 기본 단위입니다.
- 다수의 신호를 입력받아서 하나의 신호를 출력하는 구조입니다.
- 퍼셉트론은 크게 가중치-편향 연산과 활성화 함수 부분으로 나눌 수 있습니다.
- 가중치 편향 연산(가중합) : 입력한 신호에 가중치를 곱한 뒤 모두 더하는 과정
- 활성화 함수 : 가중합을 얼마만큼의 신호로 출력할지 결정하는 함수
2. 활성화 함수
퍼셉트론을 여러 신호를 입력받아서 하나의 신호를 출력하는 단위라고 설명했습니다. 다시 신체에 비유하자면, 이 신호를 최종 신체 기관에 전달할지 말지 결정하는 게이트가 필요합니다. 익숙하거나 무시할만한 자극이라면 굳이 신체 기관에 전달하지 않아도 되겠죠. 인공신경망에서 이 역할을 활성화 함수가 합니다.
- 활성화 함수는 가중치가 곱해진 입력 신호의 총합(가중합)을 얼마만큼의 신호로 출력할지 연산하는 함수입니다.
- 보통 임계값을 기준으로 출력값이 변화합니다.
- 활성화 함수 몇 가지를 소개하겠습니다.
- 계단 함수 : 계단함수는 0을 넘기면 1, 그렇지 읺으면 0을 출력합니다. 인간의 신체 기능과 가장 유사하지만 미분이 되지 않기 때문에 인공신경망에서 사용하지 않는 함수입니다.
- 시그모이드 함수 : 미분이 불가능한 계단 함수의 단점을 보완하는 함수입니다. 입력 신호에 대해 0~1 사이의 실수로 출력합니다.
- ReLu 함수 : 시그모이드 함수는 기울기 소실이 일어난다는 단점이 있습니다. 시그모이드 함수의 단점을 보완하기 위해 ReLu 함수를 사용합니다. 0을 넘기면 입력된 값을 그대로 출력하고, 그렇지 않으면 0을 출력합니다.
- softmax 함수 : 출력층에서 사용하는 활성화 함수입니다. 다중 분류 문제에 적용할 수 있도록 시그모이드 함수를 일반화한 함수입니다. 가중합을 소프트맥스 함수에 통과시키면 n개의 클래스에 대해 확률값을 반환합니다. sum(n)은 1입니다.
3. 다층 퍼셉트론
퍼셉트론과 퍼셉트론의 중요한 기능 중 하나인 활성화 함수를 알았으니 이제, 인공신경망의 구조에 대해 정리해보겠습니다. 인공 신경망은 퍼셉트론을 깊게 쌓은 모델을 일컫습니다. 퍼셉트론을 하나만 활용하면 단층 퍼셉트론이라고 부르고 두개 이상을 활용하면 다층 퍼셉트론이라고 부릅니다. 이 다층 퍼셉트론부터를 인공 신경망이라고 부르며, 딥러닝 모델이라고도 부릅니다.
그럼 굳이 퍼셉트론을 다층으로 쌓는 이유가 있어야 하겠습니다. 단층 퍼셉트론으로는 입력받는 데이터의 특징을 추출하는데 명확한 한계가 발생합니다.
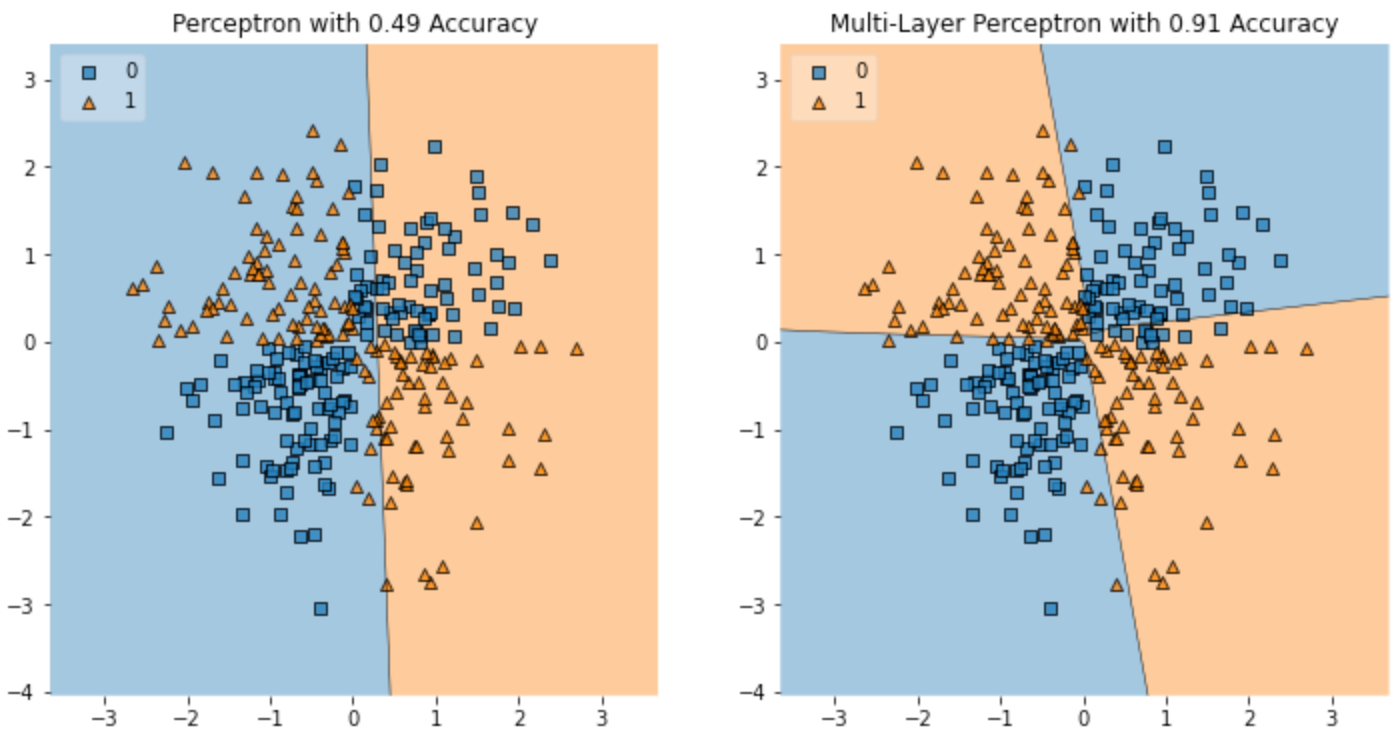
왼쪽 이미지를 보면 하나의 선으로는 위와 같은 특징의 데이터를 제대로 분할하지 못합니다. 제대로 분할하려면 적어도 두 개 이상의 선이 필요합니다. 이 하나의 선은 퍼셉트론 하나를 의미합니다. 선이 하나인 단층 퍼셉트론이 풀지 못하는 위와 같은 문제 유형을 배타적 논리합 구조라고 하며, 배타적 논리합 구조를 해결하기 위해 두 개 이상의 선을 가진 다층 퍼셉트론을 이용합니다.
1) 단층 퍼셉트론의 한계
- 단층 퍼셉트론은 활성화 함수에 의해 정해진 기준에 따라 0 또는 1을 출력합니다.
- 즉 단층 퍼셉트론은 위의 첫 번째 그래프와 같이 직선에 따라 입력된 데이터의 특성 영역을 둘로 나눕니다.
- 문제는 하나의 직선으로 입력 데이터의 특성을 나누지 못할 떄입니다.
- 배타적 논리합 구조(XOR gate)에서는 하나의 직선으로 데이터의 특성을 구분하지 못합니다.
- 이와 같은 단층 퍼셉트론의 한계를 보여주는 그래프가 두 번째 그래프입니다.
2) 단층 퍼셉트론의 한계를 극복하기 위한 다층 퍼셉트론
- 단층 퍼셉트론의 위와 같은 한계를 극복하기 위해 퍼셉트론을 다층으로 쌓아올릴 수 있습니다.
- 하나의 선으로 데이터를 구분하지 못한다면 두 번째 그래프처럼 여러개의 선을 그어 데이터를 구분하면 되기 때문입니다.
- 이를 다층 퍼셉트론이라고 부릅니다.
- model1보다 model2의 성능이 더 좋은 이유는 퍼셉트론을 다층으로 쌓아 입력된 데이터의 특징을 하나 이상의 선으로 구분했기 때문입니다. 즉, 다층 퍼셉트론을 사용하면 입력 데이터의 특징을 더욱 잘 추출할 수 있습니다.
4. 다층 퍼셉트론 구조의 인공신경망
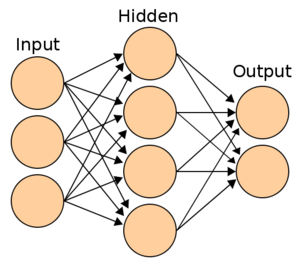
위 이미지는 2개 이상의 퍼셉트론으로 만든 2층 신경망입니다. 보통 입력층(input)은 활성화 함수가 없기 때문에 층을 셀 때 포함하지 않습니다. 기본적으로 인공신경망은 위와 같이 입력층 - 은닉층 - 출력층으로 이루어져 있습니다. 각각의 원이 하나의 퍼셉트론이며, 한 층에 1개 이상의 퍼셉트론이 있습니다. 그럼 각 층별로 어떤 일을 하는지 살펴보겠습니다.
- 입력층
- 데이터셋이 입력되는 층입니다.
- 입력되는 데이터셋의 특성에 따라 입력층 노드의 수가 결정됩니다.
- 신경망의 층수를 셀 때 입력층은 포함하지 않습니다.
- 은닉층
- 입력층으로부터 입력된 신호가 연산되는 층입니다.
- 입력층과 출력층 사이에 있는 층을 은닉층이라고 부릅니다.
- 은닉층에서 일어나는 계산의 결과를 사용자가 볼 수 없기 때문에 '은닉층'이라고 부릅니다.
- 은닉층은 데이터셋의 특성 수와 상관 없이 노드 수를 구성할 수 있습니다.
- 출력층
- 가장 마지막에 위치한 층이며 은닉층 연산을 마친 값이 출력되는 층입니다.
- 이진 분류 문제에는 시그모이드 함수를 사용합니다.
- 다중 분류 문제에는 소프트 맥스 함수를 사용합니다.
- 회귀 문제에는 활성화 함수가 없습니다. 노드 수는 출력값의 특성 수와 동일하게 설정합니다.
5. keras를 이용한 인공신경망 구현
import pandas as pd
import tensorflow as tf
#데이터 로드
mnist = tf.keras.datasets.mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
#이미지 정규화
X_train, X_test = X_train / 255.0, X_test / 255.0
#타겟값 확인
pd.unique(y_train)
#신경망 layer 구성
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape = (28, 28)),
tf.keras.layers.Dense(100, activation = 'relu'),
tf.keras.layers.Dense(10, activation = 'softmax')])
#신경망 요약
model.summary()
#모델 컴파일
#sparse_categorical_crossentropy : ordinal 형식의 다중분류 문제에 적합한 손실함수
model.compile(optimizer = 'adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
#모델 학습
model.fit(X_train, y_train, epochs=5)
# 모델 평가
model.evaluate(X_test, y_test, verbose=2)