[DL] 인공신경망 학습

지난 포스팅에서는 인공신경망의 개념과 구조에 대해 정리했습니다. 다른 머신러닝 모델과 마찬가지로 딥러닝 모델도 학습 과정이 필요한 지도 모델입니다. 입력값이 모델을 거쳐 출력되는 결과와 실제 target 간의 차이를 줄이는 학습 과정이 딥러닝 모델에도 필수입니다. 이번 포스팅에서는 인공신경망이 어떻게 신호를 학습하는지 정리해보도록 하겠습니다.

신경망 학습 과정

기본적인 신경망의 학습 과정은 다음과 같습니다. 먼저 전체적인 과정을 본 다음 하나씩 파고들어가 보겠습니다.

1. 신경망에 데이터가 입력되면 각 층에서 가중치 및 활성화 함수 연산을 반복 수행합니다.
2. 1의 과정을 모든 층에서 반복한 후에 출력층에서 계산된 값을 출력합니다.
3. 손실 함수를 사용하여 예측값과 실제값의 차이를 계산합니다.
4. 역적파 과정에서 경사하강법을 통해 각 가중치를 갱신합니다.
5. 학습 중지 기준을 만족할 때까지 1~4의 과정을 반복합니다.

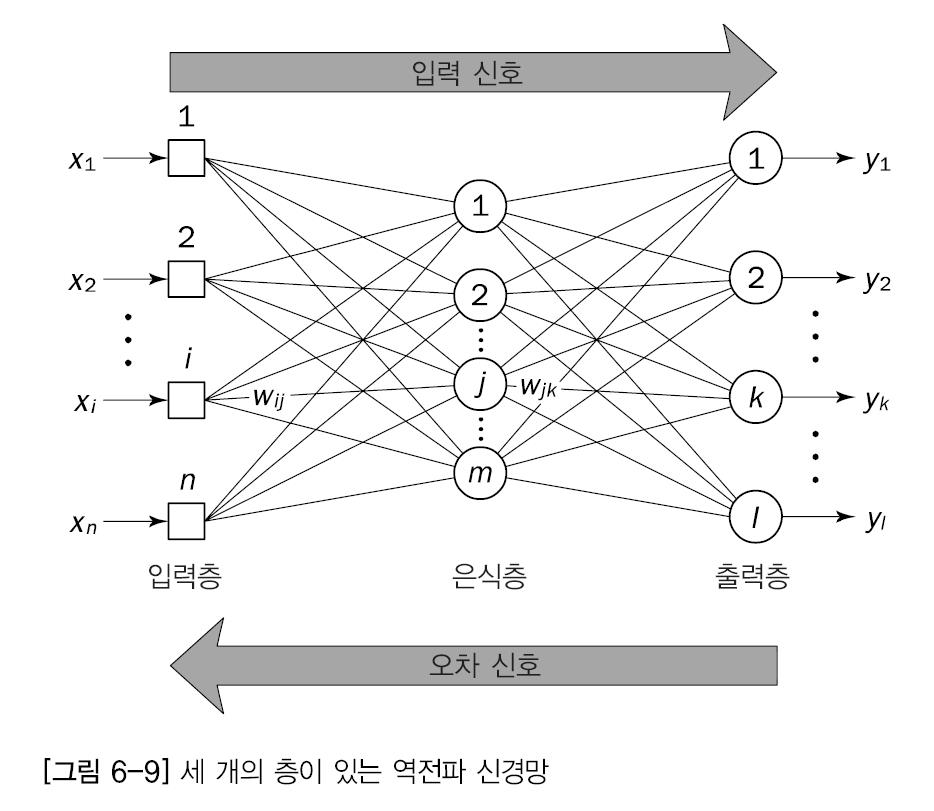
1) 순전파(1~2번 과정)

신경망 학습 과정 중 1~2번 과정을 순전파라고 부릅니다. 입력층에서 출력층까지 인공신경망의 순서대로 입력 데이터가 연산되기 때문에 순전파라고 부릅니다. 순전파 과정에서 퍼셉트론은 다수의 신호를 입력으로 받아서 가중치 연산을 거친 뒤 하나의 신호로 출력합니다.

2) 오차 연산(3번 과정)

입력층과 은닉층을 거쳐 출력층에서 최종 활성화 함수를 거치면 출력값이 나옵니다. 활성화 함수를 거쳐 최종값이 출력되면 타겟데이터와 비교하여 Loss(오차)를 계산합니다. 손실함수를 잘 정의해야 가중치가 제대로 갱신될 수 있습니다. 자주 사용하는 손실 함수 몇 가지를 소개합니다.

• Binary Crossentropy : 이진 분류에 사용하는 손실함수입니다. keras에서는 입력값으로 0 또는 1을 입력 받습니다.
• Categorical Crossentropy : 다중 분류 중 원핫인코딩 타겟값에 적용하는 손실 함수입니다.
  원핫인코딩 방식이기 때문에 '0'에 해당하는 타겟값은 loss 계산에서 사라집니다. 10개의 타겟 확률 중 하나의 값에 대한 loss func만 남게 됩니다.
• Sparse Categorical Crossentropy : 다중 분류 중 정수형 타겟값에 적용하는 손실 함수입니다. Categorical Crossentropy의 차이는 타겟값의 형식입니다.
• MeanSquaredError : 회귀에 사용하는 손실 함수입니다. 잔차를 제곱한 뒤 평균을 낸 값입니다. 잔차를 제곱하기 때문에 작은 오차에 민감한 것이 특징입니다.

3) 역전파(4번 과정)

3번 과정에서 연산한 오차를 줄이기 위해서 어떻게 해야할까요? 왔던 방향을 다시 되돌아가면서 손실을 최소화하는 방향으로 가중치와 편향을 조정해야 합니다. 중요하지 않은 특성의 가중치와 편향의 크기를 줄이는 건데요. 순서대로 살펴보겠습니다.

1. 미분으로 각 가중치가 loss에 미치는 영향(기울기)를 알 수 있음
2. loss를 0으로 만드는 방향으로 각 변수를 조정함(Gradient Dscent)
3. 미분값(기울기)가 양수이면 음의 방향으로, 음수이면 양의 방향으로 조정이 진행됨
4. 현재 가중치가 변화함에 따라 순전파의 출력값이 변하고, 역전파로 돌아올 때의 기울기도 변화하게 됨
5. 기울기가 변화한 값을 반영하게 현재 가중치가 다시 조정되고, 기울기(미분)이 0이 되어 가중치 조정이 일어나지 않을 때까지 오차역전파를 통한 가중치 조정이 진행됨

역전파는 순전파로 왔던 과정을 다시 돌아가는 과정입니다. 구해진 손실 정보를 출력층부터 입력층까지 전달해서 각 가중치를 얼마나 업데이트해야할 지 구하는 과정인데요. 이때 편미분과 Chain rule을 적용하여 각 가중치 영향력을 조정해나갑니다.

• $\frac{\partial J(\theta)}{\partial \theta_i} = \frac{\partial J(\theta)}{\partial \theta_x} \cdot \frac{\partial \theta_x}{\partial \theta_i} = \frac{\partial J(\theta)}{\partial \theta_x} \cdot \frac{\partial \theta_x}{\partial \theta_y} \cdot \frac{\partial \theta_y}{\partial \theta_i}$

출력층의 손실값인 J의 미분으로부터 식이 계속 분화하는 모습을 볼 수 있습니다. 순전파 과정에서 연산되었던 결과들이 미분되는 과정입니다. 다음 경사하강법 파트에서 이 과정을 좀 더 자세히 보겠습니다.

4) 경사하강법

경사하강법은 역전파 과정에서 타겟 값과 출력 값의 오차를 줄여나가는 방법 중 하나입니다. 매 Iteration 마다 가중치의 비용 함수를 미분하여 경사가 작아질 수 있도록 가중치를 갱신하는 방법입니다. 이때, 가중치의 비용 함수를 미분한 값이란, 가중치 매개변수의 값을 아주 조금 변화시켰을 때, 손실 함수가 어떻게 변하는지를 나타내는 구한다는 뜻입니다. 이와 같은 값을 구하는 방법을 옵티마이저라고 부르며, 경사하강법(GD)도 이 옵티마이저 중에 하나입니다.

자주 사용하는 옵티마이저를 소개하겠습니다.

• GD
  • 모든 데이터에 대한 손실 함수의 기울기를 계산한 후에 가중치를 업데이트함
  • Iteration 마다 모든 데이터를 다 사용하는 방식으로 데이터의 양이 많다면 매우 많은 시간이 걸림
• 확률적 경사 하강법(SGD)
  • 전체 데이터에서 하나의 데이터를 뽑아서 신경망에 입력한 후 손실을 계산함
  • 손실 정보를 역전파하여 신경망의 가중치를 업데이트함
  • Iteration 마다 1개의 데이터만 사용하기 때문에 가중치를 빠르게 업데이트할 수 있는 장점이 있지만, 1개의 데이터만 학습하기 때문에 극단치에 취약한 불안정한 경사 하강을 보임
• 미니 배치(Mini-batch) 경사 하강법
  • N개의 데이터로 미니 배치를 구성하여 해당 미니 배치를 신경망에 입력한 후에 이 결과를 바탕으로 가중치를 업데이트함
  • 즉 Iteration 마다 N개(=배치 사이즈)의 데이터를 사용함
  • 미니 배치의 크기를 배치 사이즈라고 하며, 일반적으로 2의 배수로 설정함
  • 데이터의 수 = Batch_size * lteration
• 모멘텀
  • GD와 SGD는 기울기가 0이 되는 지점(이전에서 가중치를 더이상 업데이트하지 않고 멈춤
  • (S)GD의 이런 특성 때문에 손실 함수가 global minimum이 아니라 local minimum에서 멈출 가능성이 높음
  • 모멘텀은 v(속도, 관성)이라는 변수에 의해서 기울기가 0이 되어도 학습을 멈추지 않고 진행 방향으로 학습을 더 진행함
• AdaGrad
  • 학습을 진행하면서 학습률을 점차 줄여가는 방법
  • 처음에는 크게 학습하다가 조금씩 작게 학습함
  • 이때 전체 학습률을 일괄적으로 낮추지 않고, 각각의 가중치 편향에 맞춰 학습률을 조정함
  • 기존 기울기 값을 제곱하여 더한 h를 역수로 취해서 학습률을 조정하는데, 많이 움직인 값은 학습률을 많이 조정한다는 뜻임
• Adam
  • AdaGrad와 모멘텀의 특징을 결합한 옵티마이저
  • global minimum을 찾는데 특화되어 있으며, 각 매개변수의 편향에도 유연하게 대처할 수 있음