[ML] 평가지표

1. R2 score

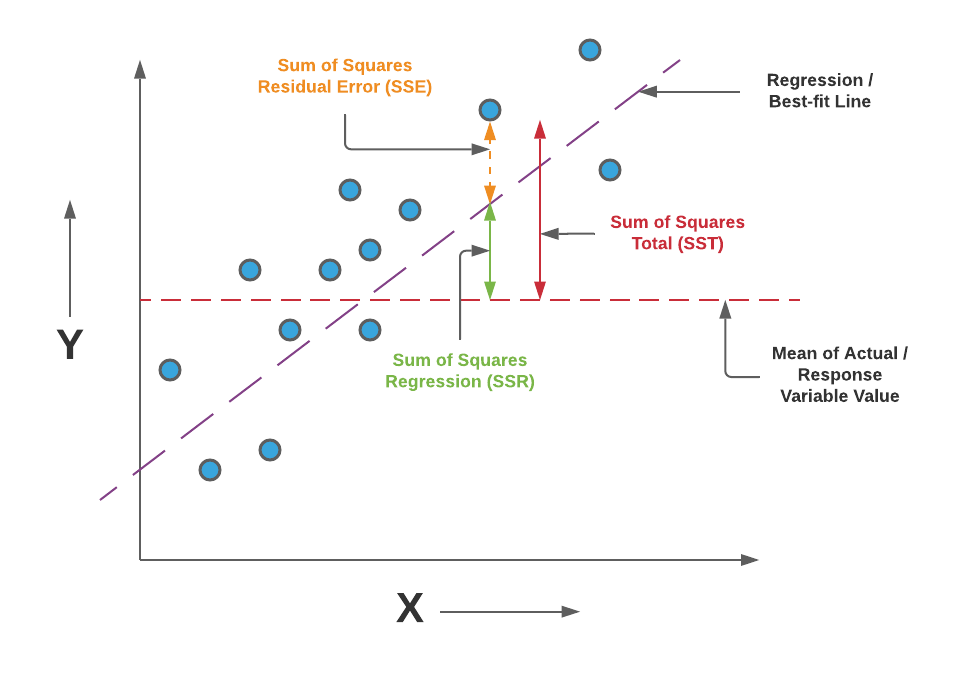
• R2(결정계수)는 회귀모델에서 사용하는 평가지표입니다. 0~1 사이의 값으로 표현되기 때문에 모델의 설명력을 직관적으로 이해할 수 있습니다.
• 데이터의 평균에서 각 데이터까지의 거리(SST)와 평균에서 각 데이터까지의 거리(SSR)의 비율을 의미합니다.
• 0~1까지로 표현되는데, 1은 두 거리가 같다는 의미로 모델과 데이터가 완전히 일치하는 것을 의미합니다.

2. MAE

• 결정계수와 마찬가지로 회귀모델을 평가할 때 자주 사용하는 평가지표입니다.
• 예측에서 실제 데이터의 차이를 절대값으로 환산하고 모두 더한 뒤 평균을 내서 계산합니다.
• 뒤에서 설명할 MSE보다 잔차에 덜 민감하지만, 스케일에 변화를 주지 않고 기존의 스케일을 그대로 활용하기 때문에 그 값을 이해하고 해석하기 쉽다는 장점이 있습니다.

3. MSE

• R2, MAE와 함께 회귀모델 평가에 사용합니다.
• 잔차를 제곱한 뒤 평균을 낸 값입니다.
• 잔차를 제곱하기 때문에 작은 오차에 민감한 것이 특징입니다.

4. RMSE

• MSE의 단점을 상쇄하기 위해 MSE에 루트를 씌운 평가지표입니다.

5. Accuracy

• 올바르게 예측한 수(TP + TN) / 전체 예측수(P+N)

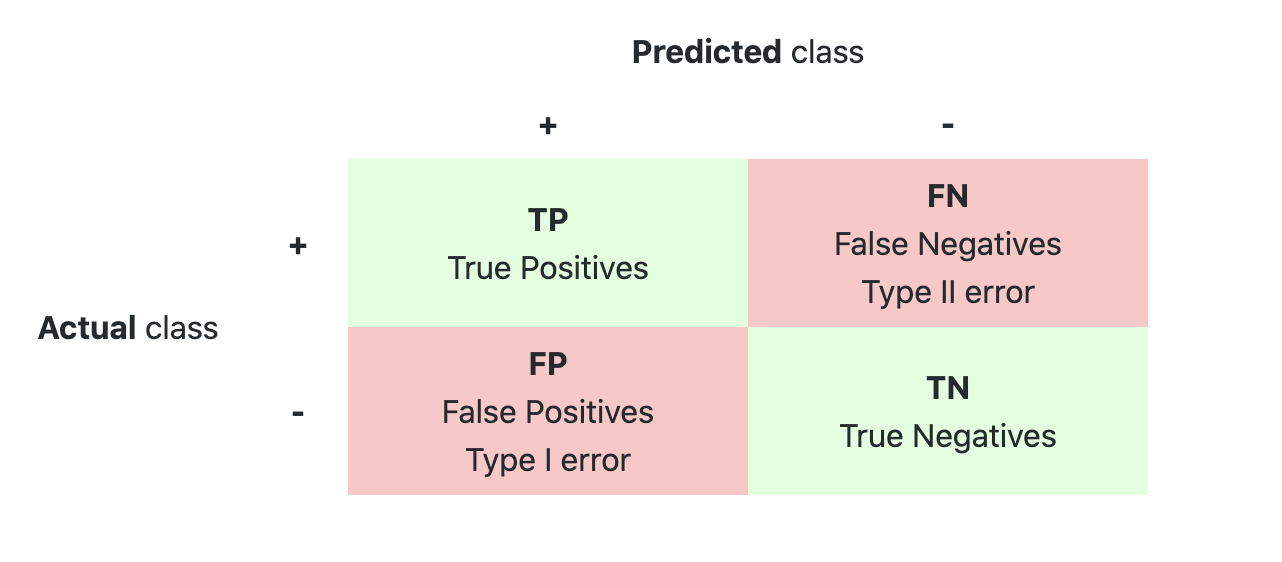
6. F1 score

• 정밀도(Precision)는 Positive로 예측한 경우 중 올바르게 Positive를 맞춘 비율입니다.
• Positive로 판단하는 임계값을 올리면 precision의 값이 올라갑니다.
• Positive 예측 기준을 올리면 더 엄밀한 기준으로 양성을 판단하기 때문입니다.
• 대신 Recall의 점수가 낮아집니다.

  $\large \frac{TP}{TP + FP}$

• 재현율(Recall)은 실제 Positive인 것 중 올바르게 Positive를 맞춘 것의 비율입니다.
• Positive로 판단하는 임계값을 낮추면 Recall의 점수가 올라갑니다.
• 기준이 낮아지면 더 많은 관측치가 양성의 범주 안에 들어오고, 그만큼 '실제 Positive'의 수가 많아지기 때문입니다.
• 대신 Recall의 점수가 낮아집니다.

  $\large \frac{TP}{TP + FN}$

• F1점수(F1 score)는 정밀도와 재현율의 조화평균입니다.
• 재현율에 정밀도의 2배 가중치를 부여하려면 beta값을 2로 조정하면 됩니다.
• 반대로 정밀도에 재현율의 2배 가중치를 부여하려면 beta값을 0.5로 조정하면 됩니다.

  • $2\cdot\large\frac{precision\cdot recall}{precision + recall}$
  • $(1+beta^2)\cdot\large\frac{precision\cdot recall}{beta^2\cdot precision + recall}$

7. ROC - AUC score

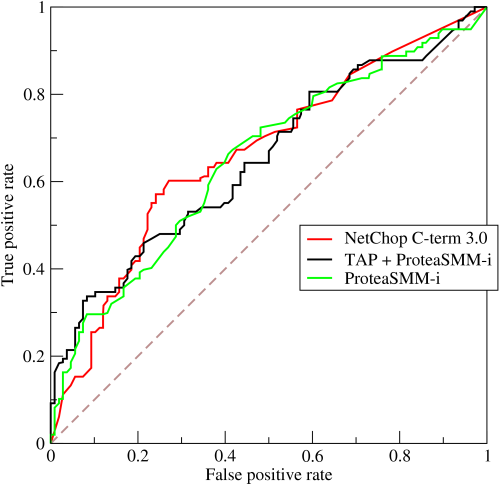
• ROC curve는 TPR(True Positive Rate)와 FPR(False Positive Rate)의 관계를 보여주는 곡선입니다.
• Positive로 판단하는 임계값을 낮추면 재현율(y축)은 상승합니다. 하지만 동시에 x축(위양성률, FPR)도 함께 상승합니다.
• 이때 ROC curve에서 위양성률은 최소화하면서 재현율을 최대화하는 지점을 찾을 수 있습니다. 그리고 그 지점의 임계값이 최적의 임계값입니다.
• AUC는 ROC curve 아래의 면적을 의미합니다. 0~1의 값을 가지며, 1에 가까울 수록 위양성률은 최소화하면서 재현율을 최대화하는 모델이라는 것을 의미합니다. 그리고 이 면적의 값을 이진분류에서 ROC-AUC score로 활용합니다.
• ROC curve는 이진분류문제에서만 사용할 수 있습니다. 다중분류문제에서는 각 클래스를 이진클래스 분류문제로 변환하여 구할 수 있습니다.

  3-class(A, B, C) 문제 -> A vs (B,C), B vs (A,C), C vs (A,B) 로 나누어 수행