
1. 단순선형회귀모델이 성립하기 위해 필요한 전제 조건
- 종속변수와 독립변수 간에 선형관계가 존재할 것
- 독립변수와 오차항 간에 상관관계가 없을 것
- 오차항의 기대값은 0
- 오차항의 분산은 모든 관찰치에서 일정할 것
- 오차항 간에 상관관계가 없을 것
- 오차항은 정규분포할 것
단순선형회귀모델의 조건은 주로 오차항에 대한 가정인데요. 오차항에 대한 가정이 대부분인 이유는 우리가 그리는 회귀선이 결국 주어진 일부의 데이터로 일종의 변수 간 경향성을 추정한 '추정된 회귀선'이기 때문입니다. 그리고 '추정된 회귀선'은 '모회귀선'과 어느정도 차이가 있을 수 밖에 없습니다. 이 차이가 오차인데요. 아래 식에서 ϵ가 이 오차를 의미합니다.
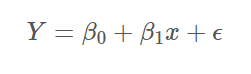
여기서 ϵ은 평균이 0이고 등분산인 정규분포를 가정합니다. 위의 모델에서 무작위로 100개의 data를 10번을 뽑으면, random noise ϵ로 인해 조금씩 다른 10개의 dataset이 뽑히게 됩니다.
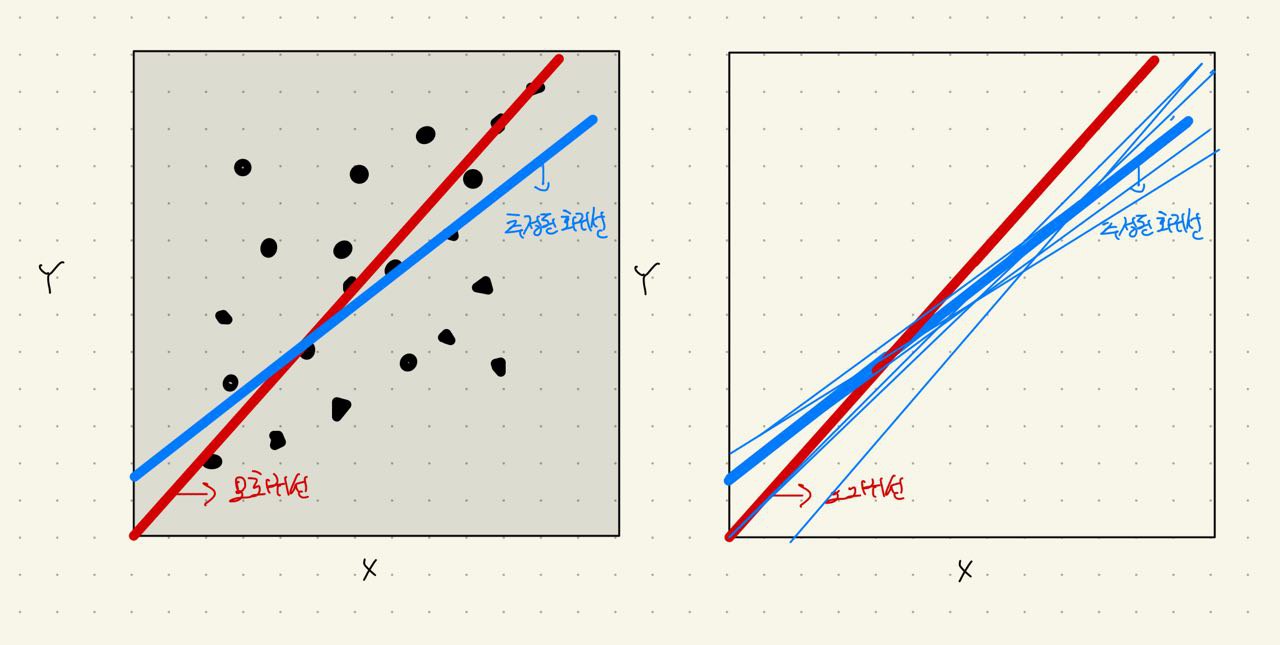
위 그림에서 빨간선이 우리가 실제로는 알지 못하는 '모회귀선'입니다. 그리고 파란선들이 우리가 Y = 2+3X+ϵ로 추정한 n개의 추정선입니다. 이 추정선들이 많아지고 평균을 낸다면 점점 '모회귀선'과 가까워질 것입니다(중심극한정리!).
그렇다면 드는 생각은 '회귀선이 어느정도 오차를 포함하고 있다면 그 모델은 얼마나 믿을만 한가?'입니다. 그리고 이 '얼마나 믿을만한가?'는 우리가 t분포에서 분산(표준편차)으로 유의확률을 구하고 귀무가설을 기각했던 것처럼 '두 변수 간에 서로 관계가 없다(=기울기가 0이다)'라는 귀무가설을 기각하는 방식으로 확인합니다.
그렇기 때문에 선형회귀 모델(더 정확히는 회귀계수. 왜냐면 기울기에 대한 가설검정을 실시한 것이기 때문에)은 신뢰구간을 통해 표현할 수 있습니다. 즉, 선형회귀의 가정이 대부분 오차항에 대한 내용인 이유는 데이터의 선형 모델을 오차항의 분산을 통해 추정하기 때문입니다.
공부하면서 선형회귀선은 오차의 분포가 아니라 오차가 최소화되는 선으로 그려지는 것 아닌가라는 생각이 들었는데, 최소제곱법 자체가 통계적 속성을 가진 방식이라고 하네요! 최소제곱법의 식을 보면 분산을 구하는 식과 유사하다는 것을 알 수 있습니다. 자유도로 나눠주는 과정만 생략되어 있네요.
그리고 위의 가정은 선형회귀선이 설득력을 갖기 위해 필요한 가정이라고 이해하면 어떨까 합니다. 오차가 최소인 지점에 선형회귀선이 그려지는 것과 별개로 선형회귀선이 설명력을 갖기 위해선 '오류는 정규분포를 따른다'라는 가정을 하고, 여기 이 오류들은 일어날 법한 일들이야라고 정당화하는 작업이 필요하다고 생각합니다. 그래야 그 회귀선을 중심으로 퍼진 오차를 정당화할 수 있으니까요.
