[ML] 과적합을 낮춰보자(1) Ridge 회귀

지난 포스팅에 이어 과적합에 대해 정리

과적합이 일어나는 이유는 Train 데이터에 대한 편향이 없기 때문이다. 즉, Train 데이터에 과적합이 일어난 모델은 Train 데이터 외에 다른 모델은 설명할 수 없다. 이 문제를 해결하기 위해서는 편향을 다소 올리더라도 Test(또는 validation) 데이터와의 분산을 줄여야 한다. 즉, Train 학습을 조금 덜 시켜서 다른 모델에도 맞을 수 있도록 조정하는 일반화/정규화/규제(regularization) 작업을 해야한다.

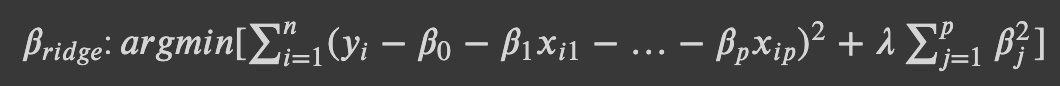
Ridge 회귀를 표현하는 함수다. 기본적인 모습은 데이터와 잔차를 최소화하는 회귀선을 찾는 최소제곱법(OLS)과 같다. 거기에 𝜆가 붙은 항이 추가되었다. 이 항을 잘 뜯어보면 𝜆 뒤에 𝛽가 붙어있다. ridge 함수의 기본 모습은 OLS라고 말했다. 즉 𝛽가 최소가 되는 값을 찾아야 하는데, 뒤에 OLS가 고려해야할 항이 하나 더 생긴 것이다.

• 만약 𝜆가 커지면? 𝜆가 커진만큼 𝛽는 작아져야 한다. 커진 𝜆를 상쇄해서 가장 작은 𝛽를 찾으려면 𝛽가 작아지는 수 밖에 없기 때문이다. 𝜆가 무한히 커지면 𝛽는 0에 수렴한다.

• 만약 𝜆가 작아지다 못해 0에 수렴하면? 𝜆가 작아진만큼 𝛽는 자유로워진다. OLS에 붙은 꼬리가 사라져 사실상 OLS 함수가 되기 때문이다.

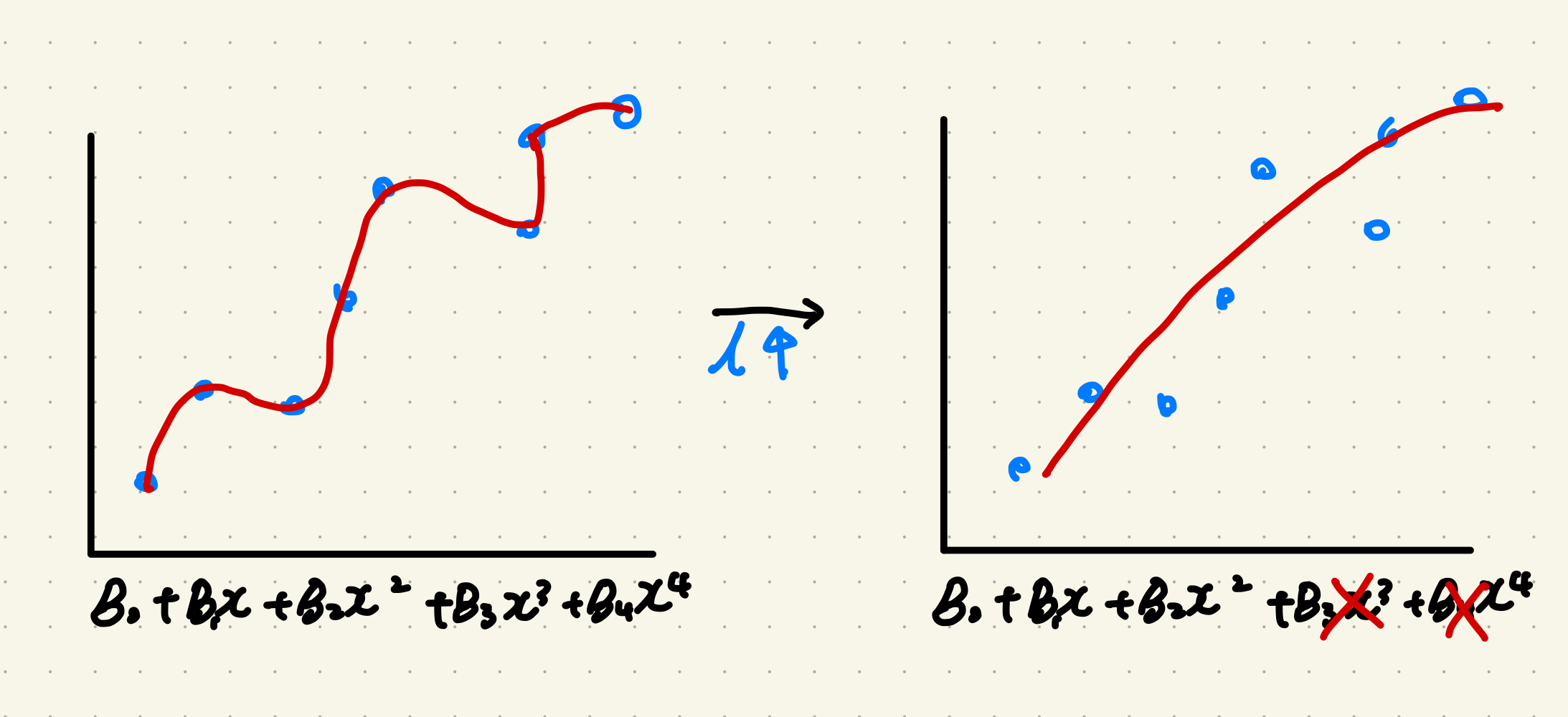
즉 𝜆는 모델의 강도를 조절하는 일종의 패널티값이다. train 데이터를 과하게 학습하면 데이터를 따라 선이 따라 움직이는 선형회귀선이 나오는데, 그 모습을 함수로 표현하면 구부러진 수만큼 차수가 높은 아주 복잡한 식이 나온다. 이때 Ridge 회귀로 𝜆을 올리면 영향력이 작은(회귀계수($b_{i}$)가 다른 $b$보다 낮은) $b$이 0에 수렴해 함수의 복잡도가 내려간다.

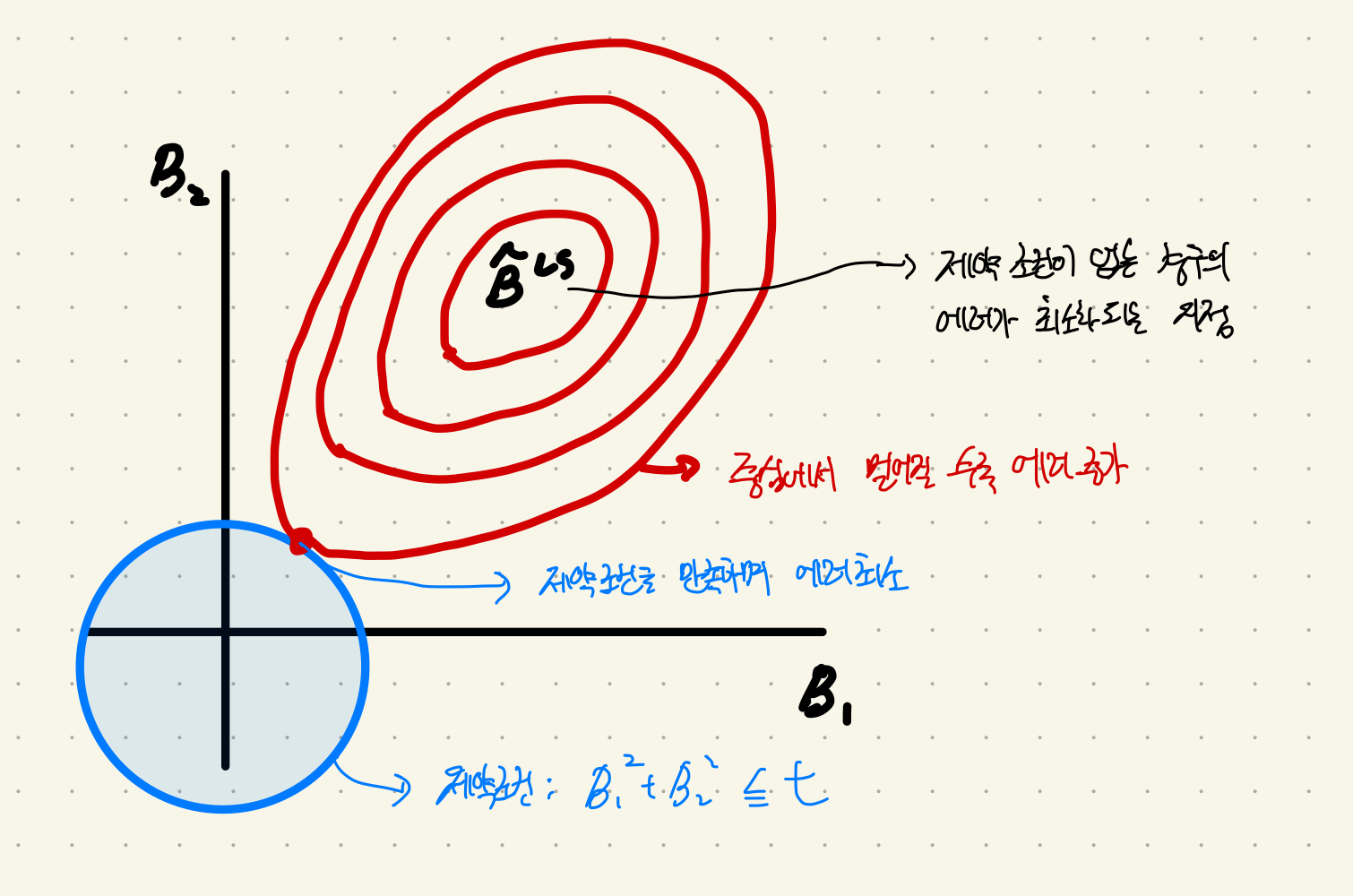
위 그림은 𝜆로 제약 조건이 걸린 OLS가 에러가 최소가 되는 지점을 찾아가는 과정이다. $L^2$ regularization은 제곱으로 제약식을 표현하기 때문에 제약조건의 모습이 원의 형태다. 반면 OLS의 함수는 타원의 모습으로 표현된다(Discriminant of conic equation).

python에서는 scikit이 ridge 회귀를 지원한다.

from sklearn.linear_model import RidgeCV

alphas = [0.01, 0.05, 0.1, 0.2, 1.0, 10.0, 100.0] #alphas = 𝜆
ridge = RidgeCV(alphas=alphas, normalize=True, cv=3) #정규화 진행, cross validation 진행
ridge.fit(X_train, Y_train)
y_pred = ridge.predict(X_test)

print("alpha: ", ridge.alpha_)
print("best score: ", ridge.best_score_)

지금까지 모델의 과적합을 낮추는 방법 중 ridge 회귀에 대해 정리했다. 다음 포스팅에서는 과적합을 낮추는 다른 방법인 feature selection에 대해 정리하겠다.