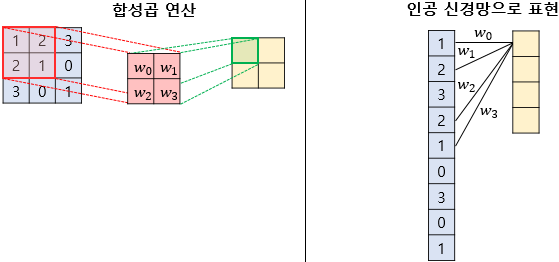
합성곱 신경망은 다층 퍼셉트론을 사용할 때보다 훨씬 적은 수의 가중치를 사용하며 공간적 구조 정보를 보존한다는 특징이 있다.
-
합성곱 신경망의 편향
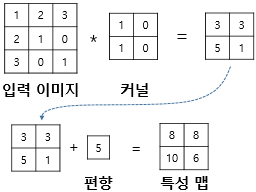
합성곱 신경망에도 편향(bias)를 당연히 추가할 수 있다. 만약, 편향을 사용한다면 커널을 적용한 뒤에 더해진다. 편향은 하나의 값만 존재하며, 커널이 적용된 결과의 모든 원소에 더해진다.
-
다수의 채널을 가질 경우의 합성곱 연산(3차원 텐서의 합성곱 연산)
다수의 채널을 가진 입력 데이터를 가지고 합성곱 연산을 한다고 하면 커널의 채널 수도 입력의 채널 수만큼 존재해야 한다. 다시 말해 입력 데이터의 채널 수와 커널의 채널 수는 같아야 한다. 채널 수가 같으므로 합성곱 연산을 채널마다 수행한다. 그리고 그 결과를 모두 더하여 최종 특성 맵을 얻는다.
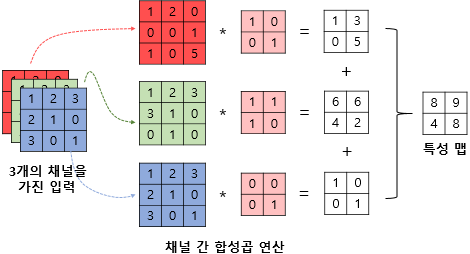
주의할 점은 위의 연산에서 사용되는 커널은 3개의 커널이 아니라 3개의 채널을 가진 1개의 커널이라는 점이다. 합성곱 연산의 결과로 얻은 특성 맵의 채널 차원은 RGB 채널 등과 같은 컬러의 의미를 담고 있지는 않는다.
하나의 입력에 여러 개의 커널을 사용하는 합성곱 연산을 할 수도 있다. 합성곱 연산에서 다수의 커널을 사용할 경우, 사용한 커널 수는 합성곱 연산의 결과로 나오는 특성 맵의 채널 수가 된다. -
풀링(Pooling)
풀링 층에서는 특성 맵을 다운샘플링하여 특성 맵의 크기를 줄이는 풀링 연산이 이루어진다. 풀링 연산에는 일반적으로 최대 풀링(max pooling)과 평균 풀링(average pooling)이 사용된다.
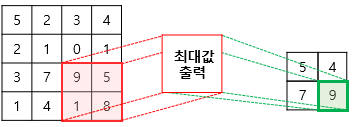
풀링 연산은 커널과 스트라이드 개념이 존재한다는 점에서 합성곱 연산과 유사하지만, 합성곱 연산과의 차이점은 학습해야 할 가중치가 없으며 연산 후에 채널 수가 변하지 않는다는 점이다.
