Attention Mechanism 용어 정리

https://wikidocs.net/22893
dot-product attention(Luong attention)을 기준으로 설명함

• Attention Score
  : 디코더의 현재 시점 t의 hidden state $s_t$를 전치(transpose)한 $s_t^T$와 인코더의 i번째 hidden state $h_i$를 내적한 값
  
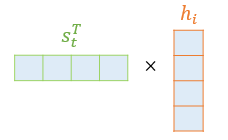
  어텐션 스코어 함수를 정의해보면 다음과 같다.
  $score(s_t, h_i) = s_t^T h_i$

• Attention Distribution(=Attention Vector)과 Attention Weight:
  : $s_t$와 인코더의 모든 hidden state의 attention score의 모음값을 $e^t$라고 정의했을 때, $e^t$의 수식은 다음과 같다.
  
  $e^t = [s_t^T h_1, ..., s_t^T h_N]$
  
  이런 $e^t$에 소프트맥수 함수를 적용하여, 모든 값을 합하면 1이 되는 확률 분포를 얻어내면 이를 어텐션 분포(attention distribution)라고 하며, 각각의 값은 attention weight라고 한다. attention distribution은 종종 attention vector라고도 불린다.
  디코더의 시점 t에서 attention weight의 모음값인 어텐션 분포를 $\alpha^t$라고 할 때, $\alpha^t$를 식으로 정의하면 다음과 같다.
  
  $\alpha^t=softmax(e^t)$
  
  

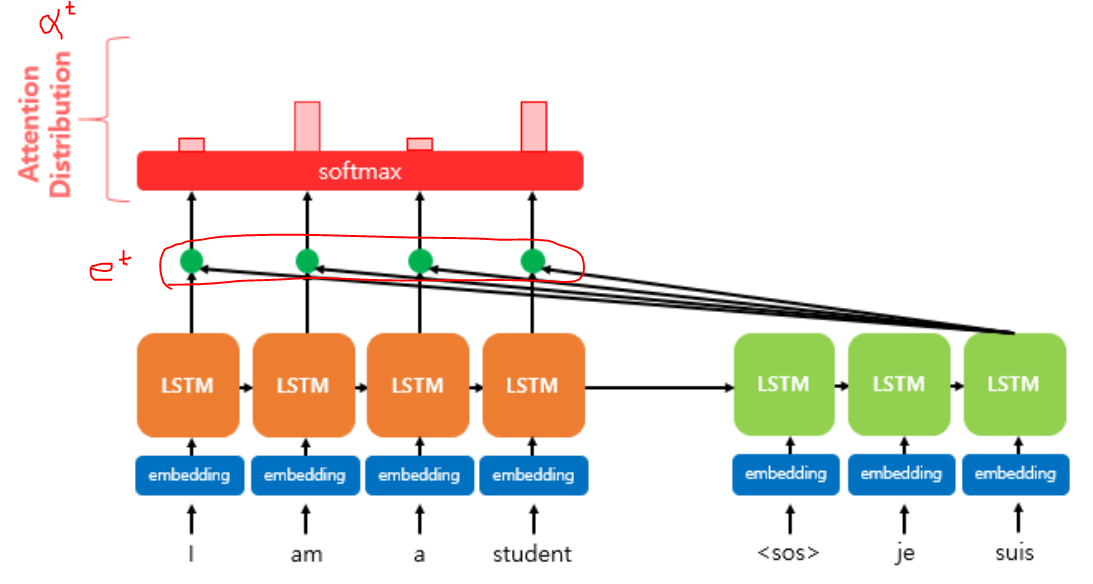
• Attention Value
  : 어텐션의 최종 결과값 attention value를 얻기 위해서 각 인코더의 hidden state와 attention weight들을 곱하고, 최종적으로 모두 더한다. 요약하면 가중합(Weighted Sum)을 진행한다.
  
  $a_t=\sum^N_{i=1}\alpha^t_i h_i$
  
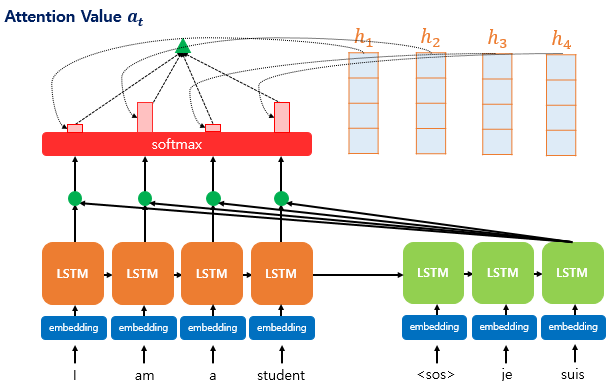
  attention value $a_t$는 디코더의 현재 시점 t에 대한 단일 vector가 된다. 이를 디코더의 t 시점의 hidden state와 concat을 해준다.
  
  
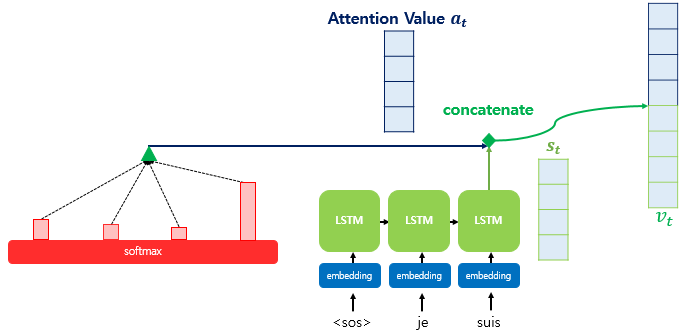
  이후
  $\tilde{s}_t=tanh(W_C[a_t;s_t]+b_c)$
  $\tilde{y}_t=Softmax(W_y \tilde{s}_t+b_y)$
  를 진행한다.
  
  

• Query, Key, Value
  : 디코더의 time t의 hidden state $s_t$가 Query가 되고
  이와 연산되어 attention score를 구하는 재료가 되는 인코더의 i번째 hidden state $h_i$가 Key,
  가중합이 진행되는 인코더의 i번째 hidden state $h_i$가 Value가 된다.