2023.01.17
이전 포스트에서 다룬 MLP 모델을 향상시켜보겠다. DeepLearning101의 3단원에 해당하는 부분들이다. 3-1부터 3-5장까지가 이에 해당하는 부분들이며 3-6은 다른 데이터셋, Fashion MNIST로 훈련을 진행해본다. 이는 아마 다른 포스트로 올라가지 않을까 싶다.
3-1. MNIST MLP Dropout
지금부터 다룰 부분들은 이전 포스트에서 다 다뤘기 때문에 달라지는 부분들만 언급하겠다. 코드를 먼저 살펴보면 다음과 같다.
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(28 * 28, 512)
self.fc2 = nn.Linear(512, 256)
self.fc3 = nn.Linear(256, 10)
self.dropout_prob = 0.5
def forward(self, x):
x = x.view(-1, 28 * 28)
x = self.fc1(x)
x = F.sigmoid(x)
x = F.dropout(x, training = self.training, p = self.dropout_prob)
x = self.fc2(x)
x = F.sigmoid(x)
x = F.dropout(x, training = self.training, p = self.dropout_prob)
x = self.fc3(x)
x = F.log_softmax(x, dim = 1)
return x보면, __init__()에서 self.dropout_prob가 생겼고 forward(x)에서는 F.dropout()라는 새로운 layer가 총 2번 더해진 것을 알 수 있다. 이 Dropout layer은 특정 확률로 계층별 뉴런을 비활성화하는 역할을 수행하는데, 여기서는 50퍼센트의 확률로 이를 진행하는 것을 뜻한다. Dropout을 쓸 때와 쓰지 않았을 때의 차이를 아래 그래프를 통해 한번 살펴보자.
아래 내용을 살펴보면, dropout을 사용하지 않은 모델의 경우 train dataset에서는 과적합이 일어나고 test data 오류가 증가하고 정확도도 향상하지 못하는 것을 알 수 있다. 하지만, dropout을 사용할 경우 비록 train dataset에서의 Loss 값은 안 했을 때보다 좋진 않지만, 과적합은 일어나지 않고 test dataset에 대한 accuracy도 더 좋은 것을 확인할 수 있다.
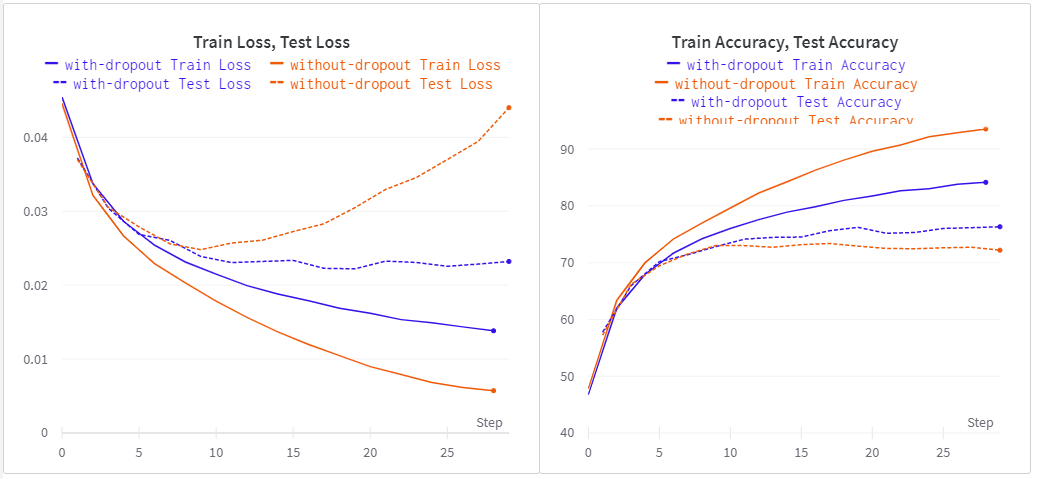
Dropout의 영향을 정리해보면 다음과 같다.
- 정규화되지 않은 네트워크는 데이터셋에 빠르게 overfit하게 된다.
- dropout을 사용하게 되면 모델이 overfitting하게 되는 것으로부터 방지하도록 돕는다. 다만, training accuracy 값이 줄어들게 되고 그것은 모델이 더 오래 훈련되어야 함을 의미한다.
- Dropout을 사용하게 되면 training accuracy는 줄어드나, 전체적인 validation accuracy는 증가하게 되면서 generalization error를 줄이는데 도움을 준다.
그래서 dropout을 사용할 경우 accuracy를 이전 모델과 비교해보면 다음과 같다. 아쉽게도, dropout을 사용했을 때 더 accuracy가 낮다. 그것은 아마 모델은 잘 정규화되어 있는데, 충분한 훈련이 부족했기에 그런 결과가 나왔을 확률이 높다. w/ dropout 그래프의 끝 부분을 보면, 그래도 accuracy가 상승하는 듯한 경향이 있긴 때문이다.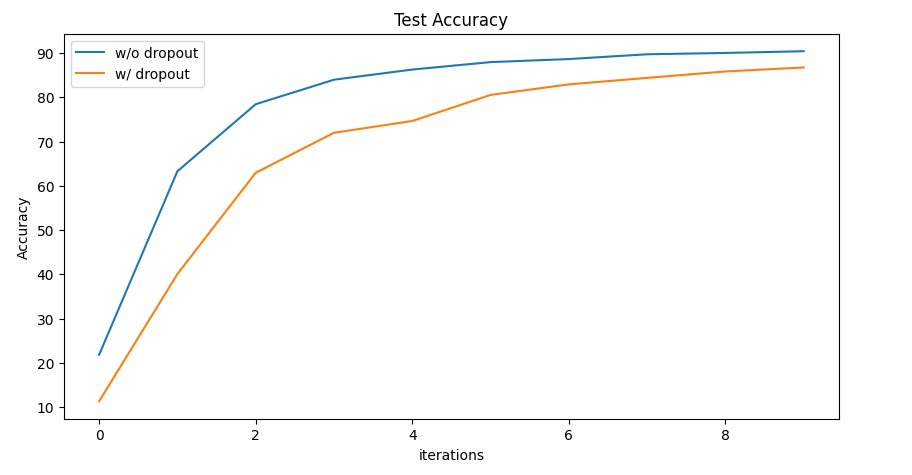
3-2. MNIST MLP Dropout ReLU
위에서 언급한 과적합 문제 말고도 다음과 같은 문제들이 발생할 수 있다.
- Gradient Vanishing
Gradient가 앞단으로 전파되면서 점점 옅어지게 되어 값이 0에 수렴하게 되는 문제이다 - Gradient Exploding
Gradient가 반대로 너무 큰 값 또는 nand값이 나오는 문제이다.
이러한 문제를 해결하기 위한 방법으로는 다음과 같은 방법들이 있다. 추가로, 출처가 자꾸 티스토리인 것은 나도 아쉽지만, 글이 깔끔하고 보기 좋게 정리되어 있어 많이 참고하게 되었다.
- Change activation function
활성화 함수 중 sigmoid에서 이 문제가 발생하기 때문에 ReLU를 사용하기도 한다. - Careful initialization
weight 초기화를 잘 해보자는 의미로, He initialization, Xavier initialization 등을 사용한다. - Small learning Rate
Gradient Exploding을 해결하기 위해 learning rate 값을 작게 할 수 있다. - Batch Normalization
학습 과정을 안전하게 할 수 있으며, 학습 속도의 가속 등 다양한 이점이 있다.
이 장에서는 활성화 함수를 바꾸는 solution에 대해 다뤄볼 것이다. 아래 코드를 보면, 모델에 ReLU 활성화함수를 sigmoid 대신에 넣어줬다.
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(28 * 28, 512)
self.fc2 = nn.Linear(512, 256)
self.fc3 = nn.Linear(256, 10)
self.dropout_prob = 0.5
def forward(self, x):
x = x.view(-1, 28 * 28)
x = self.fc1(x)
x = F.relu(x)
x = F.dropout(x, training = self.training, p = self.dropout_prob)
x = self.fc2(x)
x = F.relu(x)
x = F.dropout(x, training = self.training, p = self.dropout_prob)
x = self.fc3(x)
x = F.log_softmax(x, dim = 1)
return x보면, 모델의 설계에서 F.sigmoid(x) 대신에 F.relu(x)가 쓰이는 것을 확인할 수 있다.
ReLU 함수는 다음과 같은 꼴과 모양을 지니고 있다.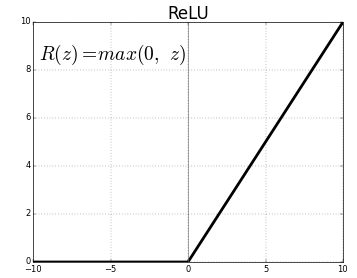
0보다 작은 값은 0을, 0보다 큰 값은 그 값 그대로 출력해주는 함수이다. 이 함수를 은닉층, hidden layer에 넣어주게 되면 기울기 소실(Gradient Vanishing) 문제가 발생하고 활성화 함수 속도가 매우 빠르다는 장점이 존재한다.
기울기 소실 문제
- ReLU 함수는 양수는 그대로, 음수는 0을 반환하기 때문에 특정 양수 값에 수렴하지 않는다.
- 따라서 심층 신경망에서 시그모이드 함수를 활성화 함수로 사용했을 때 발생했던 기울기 소실(Gradient Vanishing) 문제가 발생하지 않게 된다.
활성화 함수 속도가 매우 빠르다
- 아주 단순한 공식이다 보니, 경사 하강 시 다른 활성화 함수에 비해 학습 속도가 매우 빠르다.
- 확률적 경사하강법(SGD)을 쓴다고 할 때, 시그모이드 함수나 하이퍼볼릭 탄젠트 함수에 비해 수렴하는 속도가 약 6배 가까이 빠르다.
- ReLU가 나오기 전에 활성화 함수가 smooth(스무스)해야 가중치 업데이트가 잘 될거라고 생각하여 exp 연산이 들어간 시그모이드나 하이퍼볼릭 탄젠트 함수를 사용했으나, 활성화 함수가 smooth(스무스)한 구간에 도달하는 순간 가중치 업데이트가 매우 느려지게 된다.
- 반대로 ReLU는 편미분시 값이 1로 일정하므로, 가중치 업데이트 속도가 매우 빠르다.
장점만 있을 것 같은 이 ReLU도 단점이 존재한다고 한다.
ReLU 함수의 한계점
- 음수 값이 들어오면 모조리 0으로 반환하므로, 입력값이 음수인 경우 기울기도 모두 0이 되버린다.
- 즉, 가중치가 업데이트되다가 합이 음수가 되는 순간 ReLU는 0을 반환하기 때문에 해당 뉴런은 그 이후로 0만 반환하는 현상이 발생할 수 있다.
- 이러한 Dead Neuron을 생기는 현상을 Dying ReLU 현상이라고 한다.
- 기울기 소실 문제 방지를 위해 쓰이므로 은닉층에서만 사용하는 것을 추천한다.
- ReLU의 출력값은 0 또는 양수, 미분값은 0 또는 1로 양수 혹은 0만을 반환하므로 가중치 업데이트 시 지그제그로 최적의 가중치를 찾아가는 지그재그 현상이 발생한다.
- ReLU는 0에서 미분이 불가능하다. x->0-에서 기울기는 0, x->0+에서 기울기는 1이므로 불연속적이다. 다만 0에 걸릴 확률이 적기 때문에 이를 무시하고 사용하는 것이다.
이에 대한 보충으로 다양한 ReLU variations들이 존재하는데 이는 생략하도록 하겠다.
3-3. MNIST MLP Dropout ReLU BN
이 장에서는 Batch Nomalization layer를 더해준다.nn.BatchNorm1d()를 쓰고 batch_norm1과 batch_norm2로 표현함으로써 더해주는데 각각 1 dimension으로 512, 256이 있다..? 이 숫자에 대해서는 차차 알아봐보도록 하고 일단, 코드는 다음과 같다.
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(28 * 28, 512)
self.fc2 = nn.Linear(512, 256)
self.fc3 = nn.Linear(256, 10)
self.dropout_prob = 0.5
self.batch_norm1 = nn.BatchNorm1d(512)
self.batch_norm2 = nn.BatchNorm1d(256)
def forward(self, x):
x = x.view(-1, 28 * 28)
x = self.fc1(x)
x = self.batch_norm1(x)
x = F.relu(x)
x = F.dropout(x, training = self.training, p = self.dropout_prob)
x = self.fc2(x)
x = self.batch_norm2(x)
x = F.relu(x)
x = F.dropout(x, training = self.training, p = self.dropout_prob)
x = self.fc3(x)
x = F.log_softmax(x, dim = 1)
return xbatch nomalization은 왜 하는지 알아야 한다. 위에서 언급한 gradient를 살릴려는 의도도 있지만, Internal Covariate Shift 문제를 해결하기 위해서 쓰인다. 모델을 학습시키는 게 training dataset을 잘 학습하는 것도 있지만 그것보다 더 궁극적인 목적은 validation dataset에서 얼마나 잘 분류해내느냐에 있다. 만약 모델이 training dataset에만 치우쳐져 있으면 training dataset에서 학습한 2처럼 보이는 3을 3으로 학습한 결과 validation dataset에서 나온 2도 3으로 분류할 수 있다는 것이다. 이거는 그냥 만들어 낸 예시니까, 결론은 training dataset에 치우져진 가중치값들의 분포를 완화시켜주면서도 validation dataset에서 분류를 잘 해내도록 손을 봐줘야 하는 것이다. 그 역할을 하는 것이 바로 batch normalization인 것이다.
Covariate (공변량)이란?
공변량은 우리가 아는 독립변수, 종속변수와 같은 변수 개념이다. 보통 독립변수가 종속변수에 얼마만큼의 영향을 주는지 구하는데, 이때 대개 잡음이 섞여 독립변수와 종속변수 간의 관계를 명확하게 밝히지 못하는 경우가 많다. 이렇게 종속변수에 대해 독립변수와 기타 잡음인자들이 공유하는 변량이 바로 공변량인 것이다.
Covariate shift란?
Covariate shift는 machine learning에서 아래 그림과 같이 training data와 test data의 data distribution이 다른 현상을 의미한다. 그런 의미에서 모델을 학습시킬 때, 입력 값(독립변수, training data)에 대해 분류(종속변수, validation data)를 얼마나 잘하는지를 보고 싶은데, 이러한 관계를 분석하는 방해를 하는 요소들(covariates)의 분포가 어떤 현상에 의해 변하기 때문에 이러한 이름을 갖게 된 것이다.
모델이 위의 사진에 나와있는 training data를 학습한 후, test data를 분류하려고 할때 가중치 분포가 training data와 test data의 관점에서 동일해야 분류가 잘 될 것이다. 이게 다를 경우 overfitting이 나고 분류가 잘 이뤄지지 않게 되는 것이다.
Internal covariate shift란?
학습 과정에서 계층 별로 입력의 데이터 분포가 달라지는 현상을 의미한다. 각 계층에서 입력으로 feature를 받게 되고 그 feature는 convolution이나 fully connected 연산을 거친 뒤 activation function을 적용 받는데, 연산 전/후에 데이터 간 분포가 달라질 수 있다. Batch 단위로 학습을 시킬 경우, Batch 단위간에 데이터 분포의 차이가 존재할 수 있다. 이러한 Batch 간의 데이터 분포가 서로 다른 게 Internal Covariate Shift이다.

이러한 문제는 Batch Normalization으로 해결이 가능하다. Batch normalization은 각 배치 단위 별로 데이터가 다양한 분포를 가지더라도 각 배치별로 평균과 분산을 이용해 정규화하는 것을 뜻한다. 아래 그림을 보면 batch 단위나 layer에 따라서 입력 값의 분포가 모두 다르지마 정규화를 통해 zero mean gaussian 형태로 만들어준다. 이러한 형태가 되면 평균은 0, 표준편차는 1로 데이터의 분포를 조정할 수 있다.
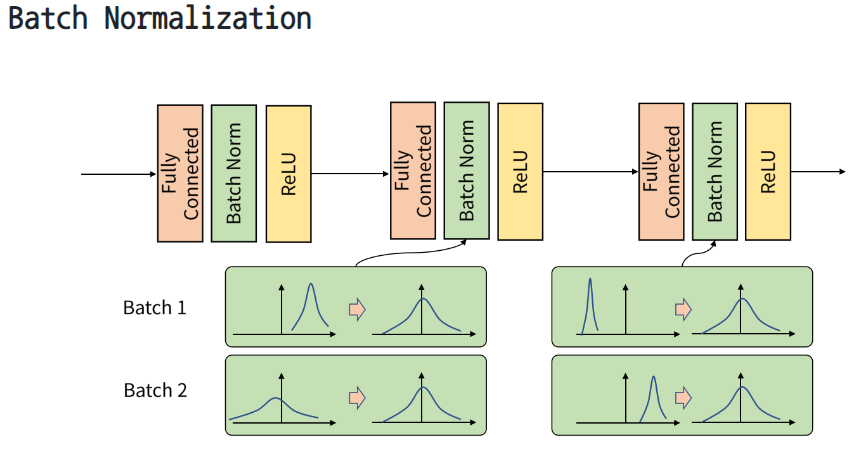
여기서 중요한 건 Batch Normalization이 학습 단계와 추론 단계에서 조금씩 다르게 적용되어야 하는 것이다.
학습 단계의 배치 정규화
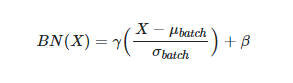
먼저 학습 단계에서는 위의 사진과 같이 정규화를 하게 된다. γ 는 스케일링 역할을 하고 β는 bias이고 이 두 값 모두 backpropagation을 통해 학습을 하게 된다.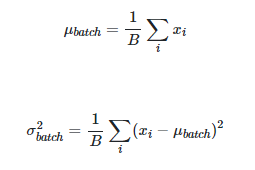

위의 사진을 보면, 평균과 분산 모두 B로 나뉘는 것을 알 수 있다. 각 배치들의 평균과 분산이 표준 정규 분포를 따르기 위함이다. 이렇게 Feature를 정규화하면 생기는 장점이 있는데, Feature들이 모두 동일한 Scale이 되어 learning rate 결정에 유리해진다. Scale이 다르면, gradient descent를 할 때, gradient가 다르게 되고 learning rate에 대해 weight마다 반응하는 정도가 달라지게 된다. gradient 간의 편차가 크면, gradient가 큰 weight은 gradient exploding, 작은 weight은 gradient vanishing 문제가 발생할 수 있다. 정규화를 통해 weight의 반응을 같게 만들어 학습에 더 유리하게 해준다. 추가적으로 normalize 단계에서 입실론이 더해지는 데, 이는 0으로 나뉘는 것을 방지하기 위해 쓰이는 것이다.
다음은 γ,β의 역할을 알아보겠다. BN은 activation function 앞에서 적용되는데, BN이 된 후 weight의 평균은 0, 분산은 1이 된다. 이 상태에서 ReLU 활성화 함수를 돌려버리면, 전체 분포에서 절반이 음수이므로 0이 되어 버린다. 기껏 정규화를 했는데 다 사라져 버리면 의미가 없어져 버리게 된다. 이러한 불상사를 방지하기 위해 γ,β가 정규화 값에 곱해지고 더해지는 것이다. 이 값들은 학습을 통해서 최적화된다.
추론 단계에서 배치 정규화
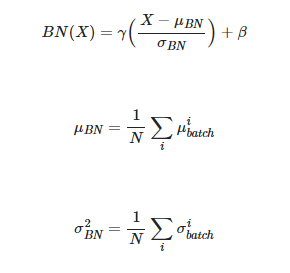
추론 과정에서는 BN에 적용할 평균과 분산에 고정값을 사용한다. 학습 단계에서는 데이터가 배치 단위로 들어와 배치의 평균/분산 값을 구하는 것이 가능하지만, 테스트 단계에서는 배치 단위로 평균/분산을 구하기가 어려워 고정된 평균/분산을 사용한다.
고정된 평균과 분산은 학습 과정에서 이동 평균(moving average) 또는 지수 평균(exponential average)을 통해 계산한 값이다. 이동 평균을 하게 되면 최근 N개 이전의 평균과 분산은 미반영되지만, 지수 평균을 이용하면 전체 데이터가 반영된다. 그리고 이때 사용되는 γ,β는 학습 과정에서 학습한 파라미터이다.
참고로 내가 참고한 사이트에 따르면 이 부분을 강조했는데, 학습 과정과 추론 과정의 알고리즘이 다르므로 framework에서 사용할 때, 학습 과정인지, 추론 과정인지에 따라 다르게 동작하도록 관리하는 것이 중요하다고 했다. 즉, 추론 과정에서는 framework의 옵션을 지정해서 평균과 분산을 moving average/variance를 사용하도록 하는 것이 중요하다고 했습니다.
Batch Normalization의 한계
Batch의 크기가 너무 작으면 잘 동작하지 않는다. 극단적인 예시로 Batch size가 1이라면 평균은 샘플 값이고 표준편차는 0이 되므로 정상적으로 normalization이 잘 되지 않을 것이다. 그리고 너무 작으면, 큰수의 법칙과 중심 극한 이론을 만족하지 못해 평균과 표준 편차가 데이터 전체 분포를 잘 표현하지 못할 수도 있다.
반대로 Batch의 크기가 너무 커도 잘 동작하지 않는다. 너무 큰 경우에는 multi modal 형태의 gaussian mixture 모델 형태가 나타날 수 있기 때문이다 (정규 분포의 봉우리가 여러개 나타나는 형태). 또한 크기가 너무 커서 병렬 연산이 비효율적일 수 있고 gradient를 계산하는 시점이 Batch 단위인데, gradient를 한번에 너무 많이 하게 되어 학습에 악영향이 있을 수 있다. 이 한계를 개선하기 위해 Weight Normalization이나 Layer Normalization을 사용할 수 있는데, 오늘은 여기까지만 하려고 한다.
PyTorch에서 사용법은?
torch.nn.BatchNorm1d나 torch.nn.BatchNorm2d가 대표적인 방법이다. 이 두가지 방법 모두 아래 식을 따른다. 특히 γ와 β는 학습되는 파라미터 이며 기본값은 γ=1,β=0을 초기값으로 학습을 시작한다. 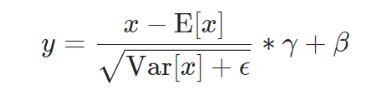
이때의 차이점은 BatchNorm1d는 Input과 Output이 (N,C) 또는 (N,C,L)의 형태를 가지고 BatchNorm2d는 (N,C,W,H)의 형태를 갖는다는 것이다. N은 Batch의 크기, C는 Channel, L은 Length를, H와 W는 각각 Height와 Width를 의미한다. BatchNorm에서 반드시 입력으로 들어가야 하는 인자는 C, 즉 Channel의 수이다. 코드 예시를 살펴보면 다음과 같다.
# With Learnable Parameters
m = nn.BatchNorm1d(100)
input = torch.randn(20, 100)
output = m(input) # print(output.size()) => torch.Size([20, 100])
# With Learnable Parameters
m = nn.BatchNorm2d(100)
input = torch.randn(20, 100, 35, 45)
output = m(input) # print(output.size()) => torch.Size([20, 100, 35, 45])Batch Normalization이 Channel을 기준으로 연산되기 때문에 Channel의 수만 맞춰주면 된다. nn.BatchNorm1d의 경우를 살펴보면 다음과 같다. 평균은 0에 가깝고 표준편차도 또한 1에 가까워진 것을 알 수 있다.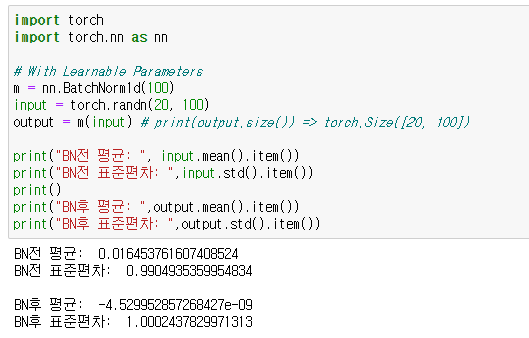
지금까지 훈련한 모델의 test accuracy는 다음과 같다. Activation function을 ReLU로 그리고 Batch Normalization을 사용한 모델의 정확도가 가장 높은 것을 알 수 있다.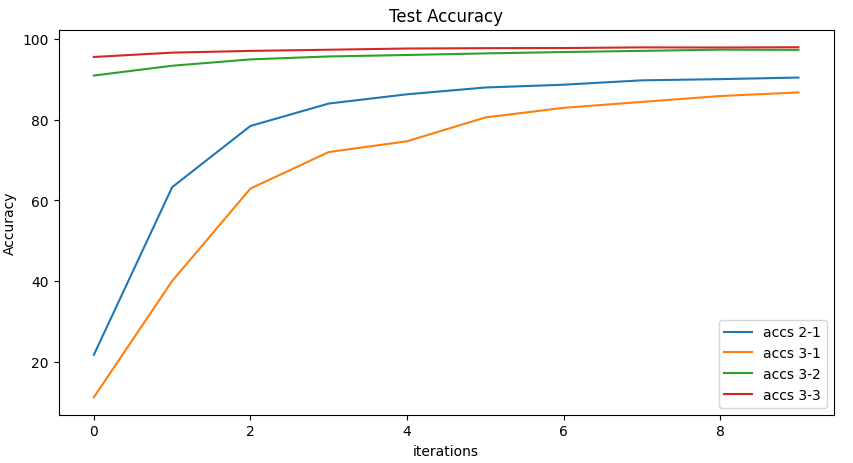
3-4. MNIST MLP Dropout ReLU BN He
모델을 훈련시킬 때, 목적함수를 최적화하기 위해 역전파를 이용해서 가중치(weight)를 조금 변화시킨다. 지금까지 가중치 값들을 변화시키는 것도 중요하지만, 가중치의 초기값도 중요하다. 초기값에 따라서 학습의 진행방향이 달라지기 때문이다. torch.nn.init.uniform_(), torch.nn.init.normal_(), torch.nn.init.xavier_uniform_() 등 다양한 초기값 function들이 존재하는데 그 중 해당 torch.nn.init.kaiming_uniform_()을 사용하고자 한다. 해당 function을 자세히 살펴보면 다음과 같은 parameter들이 존재한다. torch.nn.init.kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
하나하나 살펴보면
- tensor - an n-dimensional torch.Tensor
- a - the negative slope of the rectifier used after this layer (only used in
'leaky-relu') - mode - either
'fan-in'or'fan-out'. Choosing'fan-in'preserves the magnitude of the variance of the weights in the forward pass.'fan-out'preserves the magnitudes in the backwards pass. - nonlinearity - the non-linear function(nn.functional name), recommended to use only
'relu'or'leaky-relu'.
해당 초기화 방식은 He initialization이라고도 불리며, 무작위 초기화가 아닌 레이어의 특성을 고려한 초기화라서 Xavier Initialization과 같이 최근 자주 쓰인다.
3-5. MNIST MLP Dropout ReLU BN HE Adam
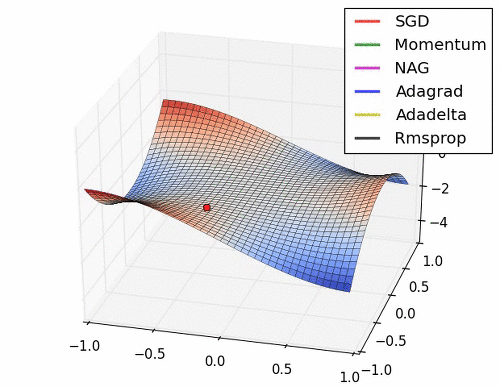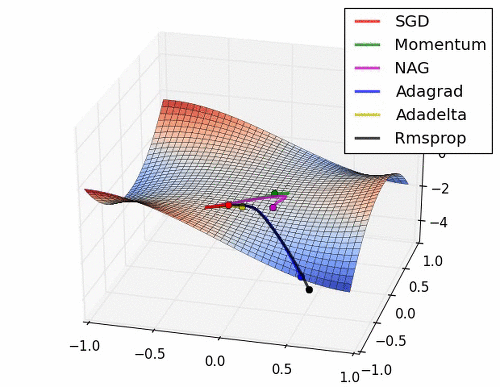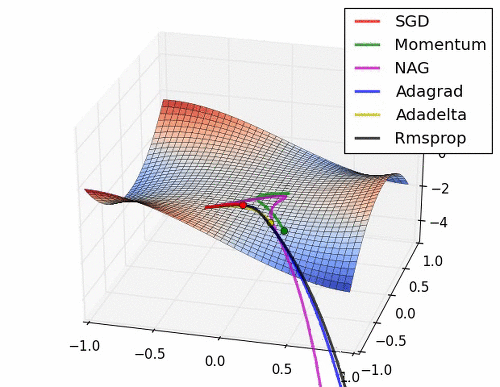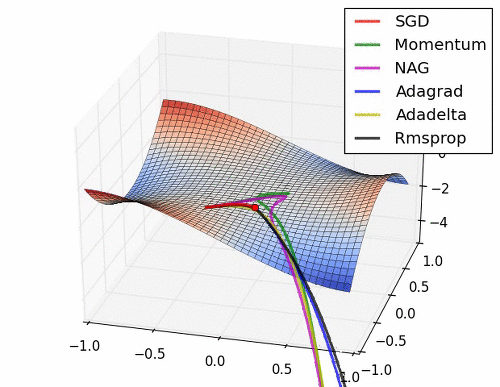
이 부분은 Optimizer에 대한 부분인데.. 내용이 복잡하다. 그래서 사진 몇 장과 움직이는 짤로 대체를 해보도록 하겠다.
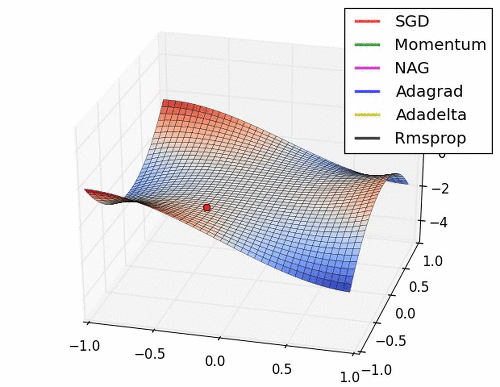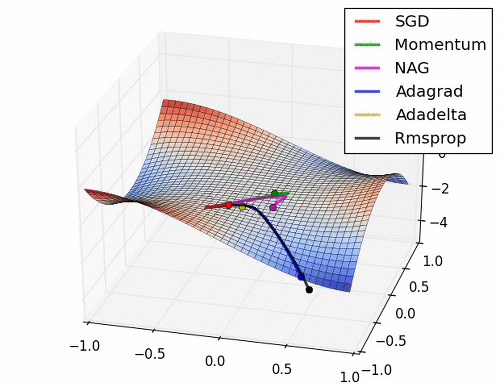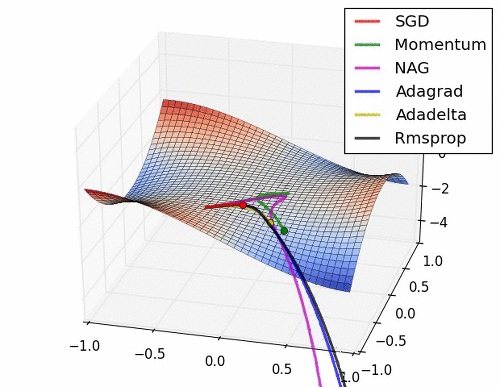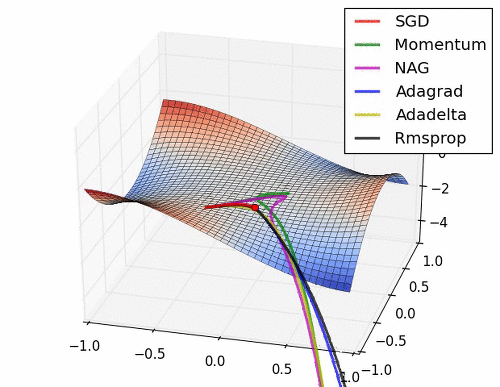
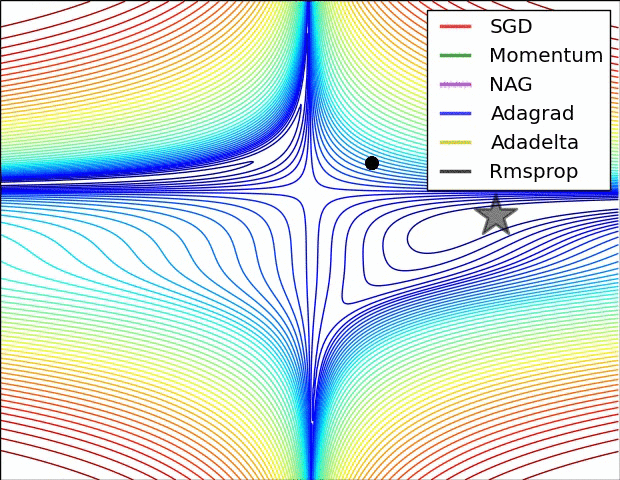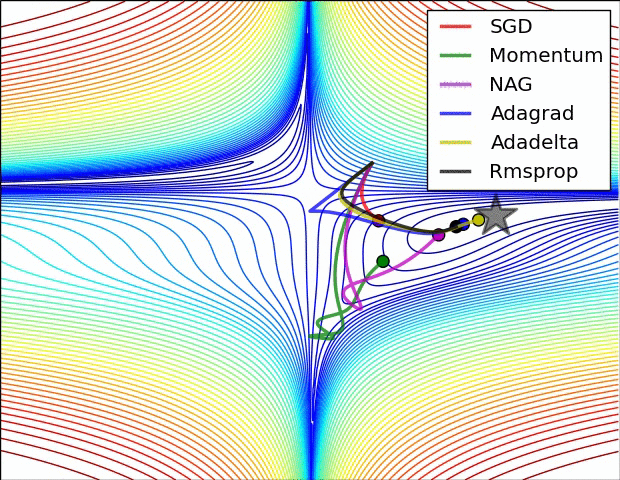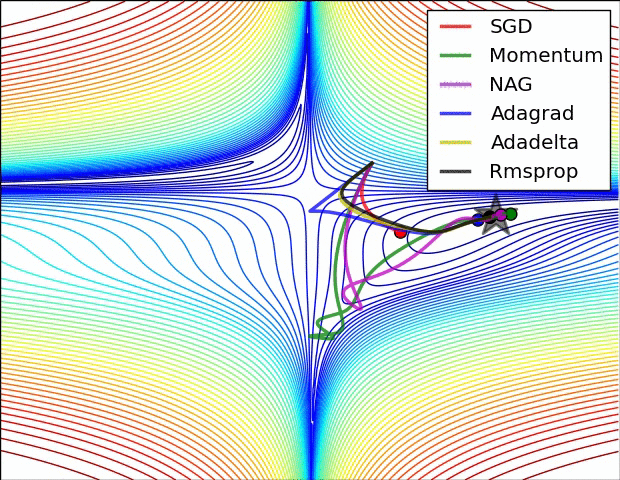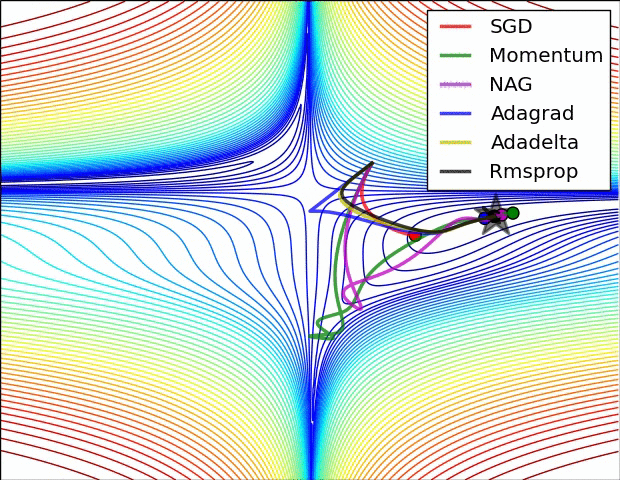
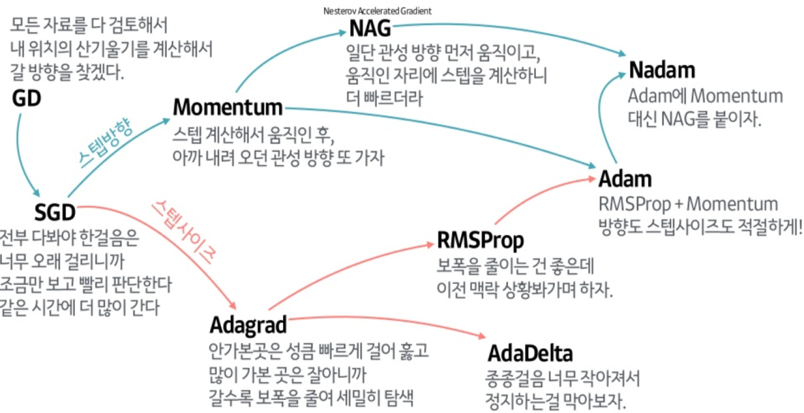
위의 사진들과 짤에서 볼 수 있듯이 SGD는 매우 느리고 다음으로는 Momentum RMSProp 등이 있다. 여기서 장점들만 가져온게 Adam이고 이 기법을 잘 쓰면 되는 것이다.
Adam 기법을 사용했을 때의 정확도 결과를 보여주겠다.
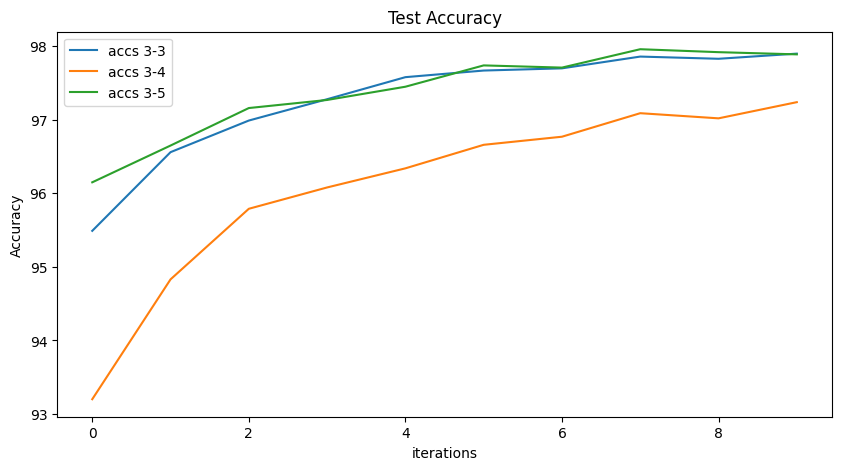
3-5가 Adam 기법을 사용했을 때인데, 처음부터 정확도가 꽤 높으며 훈련이 다 되었을 때에도 성능이 좋은 걸 확인할 수 있다.
출처
https://github.com/Justin-A/DeepLearning101
https://wandb.ai/wandb_fc/korean/reports/---VmlldzoxNDI4NzEy
https://gooopy.tistory.com/55
https://wegonnamakeit.tistory.com/47
https://89douner.tistory.com/44
https://gaussian37.github.io/dl-concept-batchnorm/
https://onevision.tistory.com/entry/Optimizer-%EC%9D%98-%EC%A2%85%EB%A5%98%EC%99%80-%ED%8A%B9%EC%84%B1-Momentum-RMSProp-Adam