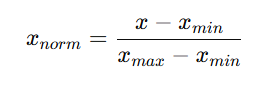데이터 분석 34일
1. 데이터 표준화와 정규화
1) Feature Scaling
- 정의: 서로
다른 단위를 가진 데이터의 값을일정한 범위나분포로 맞추는 것. - 머신러닝 모델(특히 거리 기반 알고리즘인 KNN, SVM, 등)은 변수의 크기에 민감해요.
- 예: 키(cm) = 170, 몸무게(kg) = 70 → 거리 계산 시 키의 영향이 더 커짐.
🔍 왜 표준화(Standardization)와 정규화(Normalization)가 필요할까?
머신러닝 모델은 숫자(데이터)를 기반으로 학습한다. 그런데…
- 어떤 변수는 0~1 사이,
- 어떤 변수는 0~1000 사이,
이렇게 단위나 범위가 다르면, 모델이 일부 변수에만 더 민감하게 반응하게 된다.
특히, 거리 기반 알고리즘(KNN, SVM 등)은 숫자의 크기가 직접적인 영향을 미치기 때문에
데이터의 스케일(크기)을 맞춰주는 것이 중요하다.
2) 표준화 (Standardization)
- 개념: 데이터를 평균이 0, 표준편차가 1인 형태로 바꾸는 것
- 목적: 각 데이터가 얼마나 평균에서 떨어져 있는지를 기준으로 비교
- 주로 사용되는 곳: 선형 회귀, 로지스틱 회귀, KNN 등 대부분의 통계/머신러닝 모델
공식: 𝑧 = (𝑥 − 𝜇) / 𝜎
𝑥: 원래 값, 𝜇: 평균, 𝜎: 표준편차
🔸 예시: 표준화 전 vs 표준화 후
| 항목 | 표준화 전 | 표준화 후 (평균 0, 분산 1) |
|---|---|---|
| A | 60 | -1.41 |
| B | 70 | -0.47 |
| C | 80 | 0.47 |
| D | 90 | 1.41 |
※ 평균 = 75, 표준편차 ≈ 7.07
→ 평균 기준으로 음수, 양수로 분포됨
3) 정규화 (Normalization)
- 개념: 데이터를 0에서 1 사이 범위로 바꾸는 것
- 목적: 각 데이터가 동일한 범위 안에서 비교되도록 함
- 주로 사용되는 곳: 이미지 처리, 딥러닝 입력값 등
공식:
예시:
- 시험 점수: 60점~100점 -> 내가 80점이면
(80 − 60) / (100 − 60) = 0.5
→ 중간 정도 위치
🔸 예시: 정규화 전 vs 정규화 후
| 항목 | 정규화 전 | 정규화 후 (0~1 사이) |
|---|---|---|
| A | 60 | 0.00 |
| B | 70 | 0.25 |
| C | 80 | 0.50 |
| D | 90 | 0.75 |
| E | 100 | 1.00 |
※ 최솟값 = 60, 최댓값 = 100
→ 모든 값이 0~1 사이로 변환됨
🔄 정규화 vs 표준화 요약 비교
| 구분 | 표준화 | 정규화 |
|---|---|---|
| 값 범위 | 평균 0, 표준편차 1 (음수 포함) | 0 ~ 1 |
| 계산 기준 | 평균, 표준편차 | 최솟값, 최댓값 |
| 사용 시점 | 평균,표준편차 의미 있을때, 피쳐가 정규분포를 따를 때 | 값의 절대 크기가 중요할 때, 피쳐의 분포를 모를 때 |
| 이상치 | 비교적 강함 | 매우 취약함 |
| 장점 | 정규분포 가정 시 더 안정적 | 값 범위가 고정되어 빠르게 처리 가능 |
3. 로그 변환 (Log Transformation)
- 개념: 데이터를 로그 형태로 변환해 큰 값의 영향력을 줄이는 것
- 사용 목적:
- 값의 분포가 한쪽으로 치우친 경우 → 정규분포에 가깝게 만듦
- 큰 값의 스케일을 낮추고, 데이터 분포를 평탄화
- 예시:
원래 데이터: [1, 10, 100, 1000]
로그변환 → [0, 1, 2, 3] (log10 기준)
보통 log(값 + 1) 형태로 사용 (0 처리 문제 방지)
4. KNN과 스케일링의 관계
- KNN(K-Nearest Neighbors)는 거리(유클리드 거리 등)를 기준으로 가장 가까운 이웃을 찾는 알고리즘입니다.
- 그런데 어떤 feature가 다른 feature보다 수치적으로 훨씬 크다면, 거리 계산에서 그 feature가 과도하게 큰 영향을 주게 됩니다.
🔸 예시
| 항목 | 키(cm) | 몸무게(kg) | 나이 |
|---|---|---|---|
| 사람 A | 170 | 70 | 30 |
| 사람 B | 175 | 80 | 60 |
→ 나이의 범위가 훨씬 크면 KNN은 나이 차이를 더 크게 반영해서 "가깝다 or 멀다"를 판단함
→ 이를 방지하려면 표준화나 정규화로 모든 feature의 스케일을 맞춰줘야 함
✅ 한 줄 요약!
정규화와 표준화는 모델이 공정하게 판단할 수 있도록 데이터를 '같은 눈높이'로 맞춰주는 과정이다.