1. Deep Learning
딥러닝의 구분
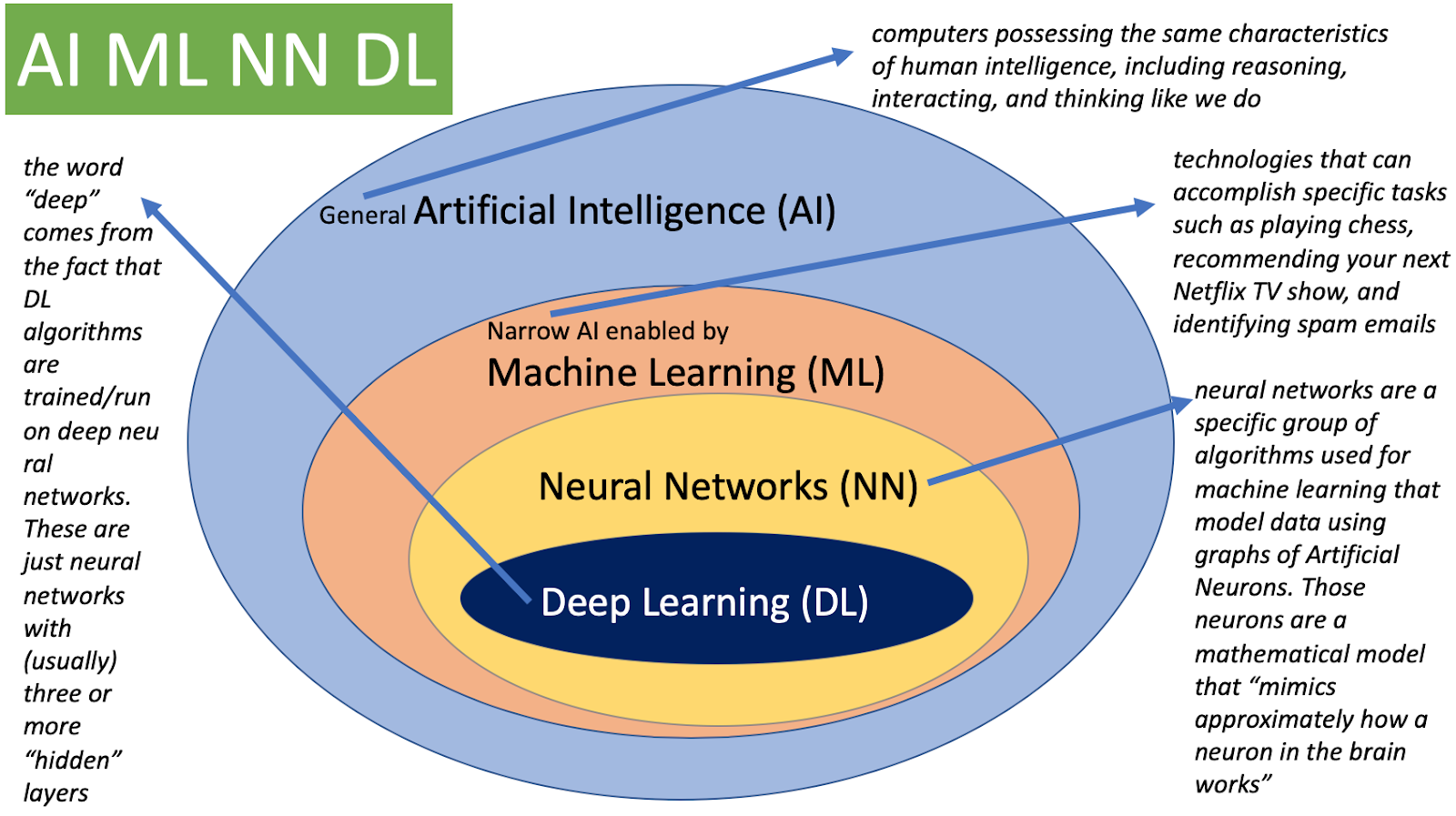
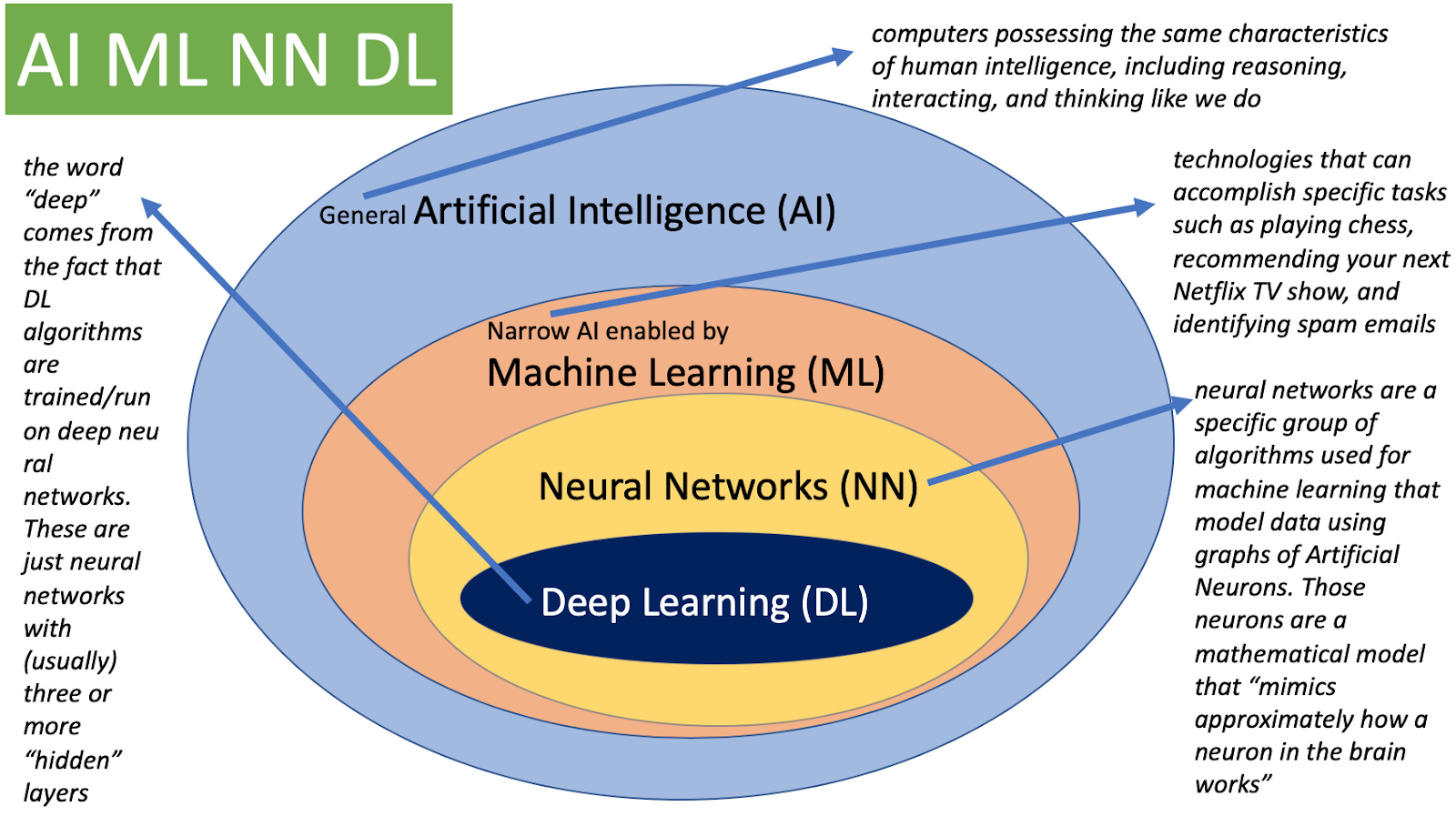
- AI (인공지능)
- Mimic human intelligence, 사람의 지능을 모방
- ML (기계학습)
- Data-driven approach, 데이터를 기반으로 무언가를 (기계)학습
- DL (딥러닝)
- Neural Networks, 그 안에서 뉴럴 네트워크를 사용하여 데이터를 가지고 무언가를 학습하는 세부 분야
딥러닝의 Key Components
- data
- the model can learn from
- model
- how to transform the data
- loss function
- quantifies the bbadness of the model
- algorithm
- to adjust the parameters to minimize the loss
- to adjust the parameters to minimize the loss
기타
- loss function을 줄이기만 하는 것이 목적이 아니라, 모델이 학습하지 않았던 테스트 데이터/실제 사용 환경에서 잘 동작하는 것이 목적..! -> 해당 parameter 값(weight, bias)을 찾는 것이 중요할 것
- 모델의 layer를 깊게 쌓으면 문제가 생기는 이유 또한, train error는 적게 나오지만, test data에서 성능이 잘 안 나오기 때문 (+ 이는 ResNet 등장 후 보완이 됨)
Neural Networks
- 인간의 뇌 구조를 모방한 구조
- 뉴럴 네트워크는 함수를 근사하는 모델(
Function Approximator) - 비선형 변환의 연속
Neural networks are function approximators that stack affine transformations followed by nonlinear transformations.
MLP(다층퍼셉트론) PyTorch로 구현해보기
- Evaluate Function 정의
Eval과정은with torch.no_grad():설정해줘야 함- 전체 Dataset에서 정의한
iterator통해, 돌면서Batch Size만큼 뽑아내며eval과정 처리 .to(device)이용해Batch Size만큼의 X 데이터/y 데이터로부터 예측 값/정답 값 정의view()함수 : 필요 시, reshape
def func_eval(model,data_iter,device):
with torch.no_grad():
model.eval() # evaluate (affects DropOut and BN)
n_total,n_correct = 0,0
for batch_in,batch_out in data_iter:
y_trgt = batch_out.to(device)
model_pred = model(batch_in.view(-1, 28*28).to(device))
_,y_pred = torch.max(model_pred.data,1)
n_correct += (y_pred == y_trgt).sum().item()
n_total += batch_in.size(0)
val_accr = (n_correct/n_total)
model.train() # back to train mode
return val_accr
print ("Done")- Train 코드
-
전체 Dataset에서 정의한
iterator통해, 돌면서Batch Size만큼 뽑아내며train과정 처리 -
[1] 포워드 과정
- (1)위에서 정의한
CustomModel의forward(self, x)함수와 (2)선택한loss함수(크로스엔트로피 등)에 배치를 돌면서피드포워드
- (1)위에서 정의한
-
[2] 옵티마이저 및 로스 업데이트 과정 (
backpropagation)- (1)
옵티마이저.zero_grad()로 값 리셋, (2)출력로스.backward()로 미분값 백워드, (3)옵티마이저.step()로 값 업데이트
- (1)
- code
print ("Start training.")
M.init_param() # initialize parameters
M.train()
EPOCHS,print_every = 10,1
for epoch in range(EPOCHS):
loss_val_sum = 0
for batch_in,batch_out in train_iter:
# Forward path
y_pred = M.forward(batch_in.view(-1, 28*28).to(device))
loss_out = loss(y_pred,batch_out.to(device))
# Update
optm.zero_grad() # reset gradient
loss_out.backward() # backpropagate
optm.step() # optimizer update
loss_val_sum += loss_out
loss_val_avg = loss_val_sum/len(train_iter)
# Print
if ((epoch%print_every)==0) or (epoch==(EPOCHS-1)):
train_accr = func_eval(M,train_iter,device)
test_accr = func_eval(M,test_iter,device)
print ("epoch:[%d] loss:[%.3f] train_accr:[%.3f] test_accr:[%.3f]."%
(epoch,loss_val_avg,train_accr,test_accr))
print ("Done") 2. Optimization
-
Generalization
- 일반화 성능을 높이자
- 학습 데이터 - 테스트 데이터 간 성능의 차이(Generalization Gap)가 적을 때를 지향
- underfitting vs. overfitting 용어와 관련
-
Cross-validations
- 학습 데이터 / 테스트 데이터를 k개로 나누어서, (k-1)개로 training, 1개로 validation 일부만 학습에 사용
- Cross-validations을 이용해 최적의 하이퍼 파라미터 값을 찾고, 이 하이퍼 파라미터 값을 가지고 모델을 학습하는 방법
-
Bias와 Variance
- 편향과 분산
- bias와 variance는 Trade-off 관계를 갖는다.
- Cost를 최소화하는 문제는, 즉, bias, variance, noise 세 가지를 최소화하는 것
- Bootstrapping
- 학습 데이터가 고정되어 있을 때, 그 안에서 subsampling을 통해서 학습 데이터를 여러 개로 만들고, 이를 통해 만든 여러 개의 모델/metric을 통해, 전체 모델의 일치성/불확실성을 파악하는 접근법
선형회귀문제(음성신호 데이터) PyTorch로 optimizer 비교해보기
- optimizers 정의
torch.optim라이브러리 활용해 선언momentum옵티마이저는momentum=(확률값)옵션 추가
- code
### 임포트 : import torch.optim as optim
LEARNING_RATE = 1e-2
# Instantiate models
model_sgd = Model(name='mlp_sgd',xdim=1,hdims=[64,64],ydim=1).to(device)
model_momentum = Model(name='mlp_momentum',xdim=1,hdims=[64,64],ydim=1).to(device)
model_adam = Model(name='mlp_adam',xdim=1,hdims=[64,64],ydim=1).to(device)
# Optimizers
loss = nn.MSELoss()
optm_sgd = optim.SGD(model_sgd.parameters(), lr=LEARNING_RATE)
optm_momentum = optim.SGD(model_momentum.parameters(), lr=LEARNING_RATE, momentum=0.9)
optm_adam = optim.Adam(model_adam.parameters(), lr=LEARNING_RATE)
print ("Done.")- 💡 인사이트
-
Adam
Adam은 짧은 학습 시간부터 성능(정확도)이 확보됨Adam에는adaptive learning개념이 반영된 접근법. (adaptive learning: 어떠한 파라미터에 대해서는 lr을 높이고, 다른 어떠한 파라미터에 대해서는 lr을 줄여나감)- 따라서, 똑같은 lr을 선언해주어도 더 빠르게 성능이 확보될 수 있다..! ✨
- Momentum
Momentum은 학습 시간이 조금 길어지면 성능 확보됨. 반면, SGD는 같은 시간까지도 성능이 확보되지 않음Momentum은 이전 배치의gradient정보를 활용해 현재 배치 턴에서 사용하겠다는 접근법- 이러한 점에서 미니배치일 때,
SGD보다 좋다..! ✨
- SGD
SGD는 데이터에서 큰 특징이 되는 파트 위주로 학습이 잘되고, 세부적으로는 잘 놓치는 모양새를 보임- 하지만,
SGD는 오랜 학습 시간이 흘렀을 때에는 더 좋은 성능을 보일 순 있다.
- 결론:
Adam/rAdam을 초기에 사용하면 어느정도의 성능을 짧은 시간에 효율적으로 확보할 수 있다..! ✨
171개의 댓글
Double your deposit with Linebet’s promo code BNB777! Claim a 100% bonus up to €130. Enjoy free spins, sports bets, and exclusive rewards today.code promo linebet cote d'ivoire
You make so many great points here that I read your article a couple of times. Your views are in accordance with my own for the most part. This is great content for your readers. 五反田 英語 アルバイト
POL88 adalah situs slot online gacor terpercaya dengan RTP tinggi dan game dari provider ternama. Daftar sekarang untuk nikmati jackpot besar serta bonus harian yang banyak. slot gacor
This article was written by a real thinking writer. I agree many of the with the solid points made by the writer. I’ll be back. jay rufer
Keep up the good work , I read few posts on this web site and I conceive that your blog is very interesting and has sets of fantastic information. agenolx
Really a great addition. I have read this marvelous post. Thanks for sharing information about it. I really like that. Thanks so lot for your convene. BATMAN138
Thank you for such a well written article. It’s full of insightful information and entertaining descriptions. Your point of view is the best among many. DeepL
This is my first time i visit here and I found so many interesting stuff in your blog especially it's discussion, thank you. sandibet
A very awesome blog post. We are really grateful for your blog post. You will find a lot of approaches after visiting your post. hptoto alternatif
A very awesome blog post. We are really grateful for your blog post. You will find a lot of approaches after visiting your post. pass prop firm
A very awesome blog post. We are really grateful for your blog post. You will find a lot of approaches after visiting your post. toto login
Thanks for a wonderful share. Your article has proved your hard work and experience you have got in this field. Brilliant .i love it reading. olxtoto
Thanks for a wonderful share. Your article has proved your hard work and experience you have got in this field. Brilliant .i love it reading. situs togel terpercaya
I’m going to read this. I’ll be sure to come back. thanks for sharing. and also This article gives the light in which we can observe the reality. this is very nice one and gives indepth information. thanks for this nice article... hptoto situs slot
Thanks for a wonderful share. Your article has proved your hard work and experience you have got in this field. Brilliant .i love it reading. sandibet
You make so many great points here that I read your article a couple of times. Your views are in accordance with my own for the most part. This is great content for your readers.olxtoto
Excellent article. Very interesting to read. I really love to read such a nice article. Thanks! keep rocking. slot qris
It was wondering if I could use this write-up on my other website, I will link it back to your website though.Great Thanks. Bulenox coupon code
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you.gaspol189
It was wondering if I could use this write-up on my other website, I will link it back to your website though.Great Thanks. bandar toto macau
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you.M88
I admire this article for the well-researched content and excellent wording. I got so involved in this material that I couldn’t stop reading. I am impressed with your work and skill. Thank you so much.situs toto
I admire this article for the well-researched content and excellent wording. I got so involved in this material that I couldn’t stop reading. I am impressed with your work and skill. Thank you so much.situs toto
I admire this article for the well-researched content and excellent wording. I got so involved in this material that I couldn’t stop reading. I am impressed with your work and skill. Thank you so much.situs toto
I admire this article for the well-researched content and excellent wording. I got so involved in this material that I couldn’t stop reading. I am impressed with your work and skill. Thank you so much.situs toto
I think this is an informative post and it is very useful and knowledgeable. therefore, I would like to thank you for the efforts you have made in writing this article.olxtoto
Thanks for a very interesting blog. What else may I get that kind of info written in such a perfect approach? I’ve a undertaking that I am simply now operating on, and I have been at the look out for such info. keluaran toto macau
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you.keytoto
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you.keytoto
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you.olxtoto
Thanks for a wonderful share. Your article has proved your hard work and experience you have got in this field. Brilliant .i love it reading. olxtoto link alternatif
Thanks for a wonderful share. Your article has proved your hard work and experience you have got in this field. Brilliant .i love it reading. toto slot 777 login
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you.olxtoto
This is my first time i visit here. I found so many interesting stuff in your blog especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the enjoyment here keep up the good worktoto togel
This is my first time i visit here and I found so many interesting stuff in your blog especially it's discussion, thank you.toto 4d
Thanks for a wonderful share. Your article has proved your hard work and experience you have got in this field. Brilliant .i love it reading. togel online
Thanks for a very interesting blog. What else may I get that kind of info written in such a perfect approach? I’ve a undertaking that I am simply now operating on, and I have been at the look out for such info.keluaran toto macau
I have read all the comments and suggestions posted by the visitors for this article are very fine,We will wait for your next article so only.Thanks! olxtoto
When your website or blog goes live for the first time, it is exciting. That is until you realize no one but you and your.kantorbola slot
Positive site, where did u come up with the information on this posting? I'm pleased I discovered it though, ill be checking back soon to find out what additional posts you include.situs toto 4d
It was wondering if I could use this write-up on my other website, I will link it back to your website though.Great Thanks. olxtoto login
Thanks For sharing this Superb article.I use this Article to show my assignment in college.it is useful For me Great Work.toto macau
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you. olxtoto
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you. jpdewa
It was wondering if I could use this write-up on my other website, I will link it back to your website though.Great Thanks. slot dax69
I haven’t any word to appreciate this post.....Really i am impressed from this post....the person who create this post it was a great human..thanks for shared this with us. olxtoto link alternatif
Wow, What a Excellent post. I really found this to much informatics. It is what i was searching for.I would like to suggest you that please keep sharing such type of info.Thankssitus slot
Wow, excellent post. I'd like to draft like this too - taking time and real hard work to make a great article. This post has encouraged me to write some posts that I am going to write soon. SoundCloud MP3
I wanted to thank you for this great read!! I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post. olxtoto link
I wanted to thank you for this great read!! I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post. toto macau
Great job for publishing such a beneficial web site. Your web log isn’t only useful but it is additionally really creative too.slot dax69
Positive site, where did u come up with the information on this posting? I'm pleased I discovered it though, ill be checking back soon to find out what additional posts you include. bandar togel terpercaya
Thanks for a very interesting blog. What else may I get that kind of info written in such a perfect approach? I’ve a undertaking that I am simply now operating on, and I have been at the look out for such info.olxtoto togel login
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you. mawartoto
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you. Lotto resmi
I was reading some of your content on this website and I conceive this internet site is really informative ! Keep on putting up. rtp olxtoto
What a fantabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much.prediksi togel online
What a fantabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much. live toto macau
What a fantabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much. olxtoto login slot
This is my first time i visit here. I found so many interesting stuff in your blog especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the enjoyment here keep up the good work olxtoto
This is my first time i visit here. I found so many interesting stuff in your blog especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the enjoyment here keep up the good work olxtoto
I admire this article for the well-researched content and excellent wording. I got so involved in this material that I couldn’t stop reading. I am impressed with your work and skill. Thank you so much有道下载.
I definitely enjoying every little bit of it. It is a great website and nice share. I want to thank you. Good job! You guys do a great blog, and have some great contents. Keep up the good work.link alternatif olxtoto
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you. สล็อตเครดิตฟรี มาใหม่
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you. olxtoto
You there, this is really good post here. Thanks for taking the time to post such valuable information. Quality content is what always gets the visitors coming.
You there, this is really good post here. Thanks for taking the time to post such valuable information. Quality content is what always gets the visitors coming.wps官网
Positive site, where did u come up with the information on this posting? I'm pleased I discovered it though, ill be checking back soon to find out what additional posts you include. วิเคราะห์บอล 7m
We have sell some products of different custom boxes.it is very useful and very low price please visits this site thanks and please share this post with your friends. agenolx, slot online
If more people that write articles really concerned themselves with writing great content like you, more readers would be interested in their writings. Thank you for caring about your content. slot If more people that write articles really concerned themselves with writing great content like you, more readers would be interested in their writings. Thank you for caring about your content.
slotDewapoker[https://www.oraka2.com/properties14-6](부산 출장마사지)[https://www.oraka2.com/properties-1-4](대구 출장마사지)[https://www.oraka2.com/properties14-4](광주 출장마사지)https://www.oraka2.com/properties14-5
What a fantabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much. 토토커뮤니티
What a fantabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much. سایت شرط بندی فارسی
Hey There. I found your blog using msn. This is a very well written article. I’ll be sure to bookmark it and come back to read more of your useful info. Thanks for the post. I’ll definitely return. olxtoto slot Hey There. I found your blog using msn. This is a very well written article. I’ll be sure to bookmark it and come back to read more of your useful info. Thanks for the post. I’ll definitely return. olxtoto alternatif Hey There. I found your blog using msn. This is a very well written article. I’ll be sure to bookmark it and come back to read more of your useful info. Thanks for the post. I’ll definitely return. bebtoto login Hey There. I found your blog using msn. This is a very well written article. I’ll be sure to bookmark it and come back to read more of your useful info. Thanks for the post. I’ll definitely return. slot online dana Hey There. I found your blog using msn. This is a very well written article. I’ll be sure to bookmark it and come back to read more of your useful info. Thanks for the post. I’ll definitely return. pengeluaran macau Hey There. I found your blog using msn. This is a very well written article. I’ll be sure to bookmark it and come back to read more of your useful info. Thanks for the post. I’ll definitely return. toto togel 4d
Took me time to read all the comments, but I really enjoyed the article. It proved to be Very helpful to me and I am sure to all the commenters here! It’s always nice when you can not only be informed, but also entertained! social media management
Took me time to read all the comments, but I really enjoyed the article. It proved to be Very helpful to me and I am sure to all the commenters here! It’s always nice when you can not only be informed, but also entertained! social media management
Took me time to read all the comments, but I really enjoyed the article. It proved to be Very helpful to me and I am sure to all the commenters here! It’s always nice when you can not only be informed, but also entertained! Seafood Buffet Bangkok
What a fantabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much. schlüsselfertige Renovierung
Took me time to read all the comments, but I really enjoyed the article. It proved to be Very helpful to me and I am sure to all the commenters here! It’s always nice when you can not only be informed, but also entertained! Live casino games India
Took me time to read all the comments, but I really enjoyed the article. It proved to be Very helpful to me and I am sure to all the commenters here! It’s always nice when you can not only be informed, but also entertained! betting sites
Took me time to read all the comments, but I really enjoyed the article. It proved to be Very helpful to me and I am sure to all the commenters here! It’s always nice when you can not only be informed, but also entertained! GullyBet payment options
Took me time to read all the comments, but I really enjoyed the article. It proved to be Very helpful to me and I am sure to all the commenters here! It’s always nice when you can not only be informed, but also entertained! Gullybet
I was reading some of your content on this website and I conceive this internet site is really informative ! Keep on putting up. result macau
It is a great website.. The Design looks very good.. Keep working like that!.custom plush keychain singapore
I admire this article for the well-researched content and excellent wording. I got so involved in this material that I couldn’t stop reading. I am impressed with your work and skill. Thank you so much.keluaran sydney lotto
I found so many interesting stuff in your blog especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the enjoyment here! keep up the good work... slot online
I found so many interesting stuff in your blog especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the enjoyment here! keep up the good work... toto slot
Excellent post. I was reviewing this blog continuously, and I am impressed! Extremely helpful information especially this page. Thank you and good luck.situs slot gacor
What a fantabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much. 토토커뮤니티
Positive site, where did u come up with the information on this posting? I'm pleased I discovered it though, ill be checking back soon to find out what additional posts you include.4D
Took me time to read all the comments, but I really enjoyed the article. It proved to be Very helpful to me and I am sure to all the commenters here! It’s always nice when you can not only be informed, but also entertained! limo hire
You have a real ability for writing unique content. I like how you think and the way you represent your views in this article. I agree with your way of thinking. Thank you for sharing.macau jitu This is very interesting content! I have thoroughly enjoyed reading your points and have come to the conclusion that you are right about many of them. You are great. casino88 If you set out to make me think today; mission accomplished! I really like your writing style and how you express your ideas. Thank you. situs slot gacor Thank you for such a well written article. It’s full of insightful information and entertaining descriptions. Your point of view is the best among many. olxtoto alternatif Hey There. I found your blog using msn. This is a very well written article. I’ll be sure to bookmark it and come back to read more of your useful info. Thanks for the post. I’ll definitely return. toto toge Hey There. I found your blog using msn. This is a very well written article. I’ll be sure to bookmark it and come back to read more of your useful info. Thanks for the post. I’ll definitely return. situs toto 176 login
I was reading some of your content on this website and I conceive this internet site is really informative ! Keep on putting up. data sgp
I was reading some of your content on this website and I conceive this internet site is really informative ! Keep on putting up. flowers rio de janeiro
This particular is usually apparently essential and moreover outstanding truth along with for sure fair-minded and moreover admittedly useful My business is looking to find in advance designed for this specific useful stuffs… flowers rio de janeiro
This particular is usually apparently essential and moreover outstanding truth along with for sure fair-minded and moreover admittedly useful My business is looking to find in advance designed for this specific useful stuffs… data sgp
I was reading some of your content on this website and I conceive this internet site is really informative ! Keep on putting up. 토토커뮤니티
I was reading some of your content on this website and I conceive this internet site is really informative ! Keep on putting up. live draw sgp
This particular papers fabulous, and My spouse and i enjoy each of the perform that you have placed into this. I’m sure that you will be making a really useful place. I has been additionally pleased. Good perform! gọi video riêng tư
I found so many interesting stuff in your blog especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the enjoyment here! keep up the good work... slot demo
Excellent .. Amazing .. I’ll bookmark your blog and take the feeds also…I’m happy to find so many useful info here in the post, we need work out more techniques in this regard, thanks for sharing.agen togel
We are really grateful for your blog post. You will find a lot of approaches after visiting your post. I was exactly searching for. Thanks for such post and please keep it up. Great work.miototo togel
Nice post! This is a very nice blog that I will definitively come back to more times this year! Thanks for informative post. 다낭 골프
I am happy to find this post very useful for me, as it contains lot of information. I always prefer to read the quality content and this thing I found in you post. Thanks for sharing.keytoto login
I have seen some great stuff here. Worth bookmarking for revisiting. I surprise how much effort you put to create such a great informative website. Your work is truly appreciated around the clock and the globe.kiko toto
This is such a great resource that you are providing and you give it away for free. I love seeing blog that understand the value of providing a quality resource for free. 먹튀보증 ~~
This is such a great resource that you are providing and you give it away for free. I love seeing blog that understand the value of providing a quality resource for free. situs toto 176
Took me time to read all the comments, but I really enjoyed the article. It proved to be Very helpful to me and I am sure to all the commenters here! It’s always nice when you can not only be informed, but also entertained!베트남유흥
I have read your article, it is very informative and helpful for me.I admire the valuable information you offer in your articles. Thanks for posting it.. 오피스타
It is a good site post without fail. Not too many people would actually, the way you just did. I am impressed that there is so much information about this subject that has been uncovered and you’ve defeated yourself this time, with so much quality. Good Works!situs toto login link alternatif
Excellent blog! I found it while surfing around on Google. Content of this page is unique as well as well researched. Appreciate it.harga toto
Thanks so much for this information. I have to let you know I concur on several of the points you make here and others may require some further review, but I can see your viewpoint.
olxtoto
신용카드 현금화
hp toto
هات بت انفجار
toto togel
toto 4d
All your hard work is much appreciated. Nobody can stop to admire you. Lots of appreciation.harga toto
I recently came across your blog and have been reading along. I thought I would leave my first comment. I don't know what to say except that I have enjoyed reading. Nice blog. I will keep visiting this blog very often. mawartoto resmi
Your work is truly appreciated round the clock and the globe. It is incredibly a comprehensive and helpful blog.seo optimization services
This is such a great resource that you are providing and you give it away for free. I love seeing blog that understand the value of providing a quality resource for free. 역삼오피
This article was written by a real thinking writer. I agree many of the with the solid points made by the writer. I’ll be back. data toto macau
I went to this website, and I believe that you have a plenty of excellent information, I have saved your site to my bookmarks. 오피스타 텔레그램
i read a lot of stuff and i found that the way of writing to clearifing that exactly want to say was very goo
bandar slot online
bocoran macau
4D
keytoto daftar
toto slot
olxtoto 4d
Thanks for the blog loaded with so many information. Stopping by your blog helped me to get what I was looking for. link situs toto
Thank you because you have been willing to share information with us. we will always appreciate all you have done here because I know you are very concerned with our. explicit definition
Thank you because you have been willing to share information with us. we will always appreciate all you have done here because I know you are very concerned with our. 토토프레이
I have bookmarked your blog, the articles are way better than other similar blogs.. thanks for a great blog! olxtoto
You make so many great points here that I read your article a couple of times. Your views are in accordance with my own for the most part. This is great content for your readers. data macau I admire this article for the well-researched content and excellent wording. I got so involved in this material that I couldn’t stop reading. I am impressed with your work and skill. Thank you so much. koi toto Thanks so much for this information. I have to let you know I concur on several of the points you make here and others may require some further review, but I can see your viewpoint. pol88 Very good written article. It will be supportive to anyone who utilizes it, including me. Keep doing what you are doing – can’r wait to read more posts. olxtoto Awesome article! I want people to know just how good this information is in your article. It’s interesting, compelling content. Your views are much like my own concerning this subject. togel online Awesome article! I want people to know just how good this information is in your article. It’s interesting, compelling content. Your views are much like my own concerning this subject. situs toto 176
I admit, I have not been on this web page in a long time... however it was another joy to see It is such an important topic and ignored by so many, even professionals. I thank you to help making people more aware of possible issues.paito sydney lotto
This blog is so nice to me. I will keep on coming here again and again. Visit my link as well..hptoto
This site that has articles as good as this is really worth looking at continuously.
Visit : https://mbcslot88.me/
This site that has articles as good as this is really worth looking at continuously.
Visit : https://mbcslot88.me/
This site that has articles as good as this is really worth looking at continuously.
Visit : https://mbcslot88.me/
Very informative post! There is a lot of information here that can help any business get started with a successful social networking campaign. 오피스타
Very informative post! There is a lot of information here that can help any business get started with a successful social networking campaign. Apex Trader Funding rules
Very informative post! There is a lot of information here that can help any business get started with a successful social networking campaign. kingkong4d
Hey what a brilliant post I have come across and believe me I have been searching out for this similar kind of post for past a week and hardly came across this. Thank you very much and will look for more postings from you.slot online
Positive site, where did u come up with the information on this posting?I have read a few of the articles on your website now, and I really like your style. Thanks a million and please keep up the effective work.pestoto
Your blog provided us with valuable information to work with. Each & every tips of your post are awesome. Thanks a lot for sharing. Keep blogging..pestoto
I admire this article for the well-researched content and excellent wording. I got so involved in this material that I couldn’t stop reading. I am impressed with your work and skill. Thank you so much.slot gacor
I wanted to thank you for this excellent read!! I definitely loved every little bit of it. I have you bookmarked your site to check out the new stuff you post.togel online
I would like to say that this blog really convinced me to do it! Thanks, very good post.pestoto togel
Wow, What a Excellent post. I really found this to much informatics. It is what i was searching for.I would like to suggest you that please keep sharing such type of info.Thankspestoto link
Just admiring your work and wondering how you managed this blog so well. It’s so remarkable that I can't afford to not go through this valuable information whenever I surf the internet!edctoto login
You make so many great points here that I read your article a couple of times. Your views are in accordance with my own for the most part. This is great content for your readers.سایت melbet
Thanks for the blog loaded with so many information. Stopping by your blog helped me to get what I was looking for.سایت رومابت
I recently found many useful information in your website especially this blog page. Among the lots of comments on your articles. Thanks for sharing.slot 4d
Positive site, where did u come up with the information on this posting?I have read a few of the articles on your website now, and I really like your style. Thanks a million and please keep up the effective work.오피스타
I am thankful to you for sharing this plethora of useful information. I found this resource utmost beneficial for me. Thanks a lot for hard work. Situs Toto You delivered such an impressive piece to read, giving every subject enlightenment for us to gain information. Thanks for sharing such information with us due to which my several concepts have been cleared. situs toto Wonderful article. Fascinating to read. I love to read such an excellent article. Thanks! It has made my task more and extra easy. Keep rocking. slot toto Thanks for an interesting blog. What else may I get that sort of info written in such a perfect approach? I have an undertaking that I am just now operating on, and I have been on the lookout for such info. Toto xl
This is such a great resource that you are providing and you give it away for free. I love seeing blog that understand the value of providing a quality resource for free.alexistogel
I have seen some great stuff here. Worth bookmarking for revisiting. I surprise how much effort you put to create such a great informative website. Your work is truly appreciated around the clock and the globe. basket 168
I just couldn't leave your website before telling you that I truly enjoyed the top quality info you present to your visitors? Will be back again frequently to check up on new posts.부산 출장마사지
I just couldn't leave your website before telling you that I truly enjoyed the top quality info you present to your visitors? Will be back again frequently to check up on new posts.giftcardmall
[Cool stuff you have got and you keep update all of us.](slot toto gacor)[https://planeta-animal.org/](rtp olxtoto)[https://goodthingsbeauty.com/](olxtoto slot)[https://createwowmedia.com/](link alternatif situs toto)[https://bokehmasterskit.com/](bandar toto macau)[https://www.alessandrocolla.com/first-event-storming-experiment/](daftar togel)[https://dawgyawp.com/]
Nice to read your article! I am looking forward to sharing your adventures and experiences.slot maxwin
Nice to read your article! I am looking forward to sharing your adventures and experiences.Włoska muzyka
Nice to read your article! I am looking forward to sharing your adventures and experiences.ratu777
Nice to read your article! I am looking forward to sharing your adventures and experiences.link alternatif tok99toto
Nice to read your article! I am looking forward to sharing your adventures and experiences.daftar keongwin
The website is looking bit flashy and it catches the visitors eyes. Design is pretty simple and a good user friendly interface.실시간무료바카라
The website is looking bit flashy and it catches the visitors eyes. Design is pretty simple and a good user friendly interface.olxtoto
The website is looking bit flashy and it catches the visitors eyes. Design is pretty simple and a good user friendly interface.olxtoto
Carry on the great operate, My spouse and i go through number of blogposts for this site along with I do think that your particular world wide web web site can be true exciting and possesses acquired encircles involving amazing data. 신용카드현금화
This is such a great resource that you are providing and you give it away for free. I love seeing blog that understand the value. Im glad to have found this post as its such an interesting one! I am always on the lookout for quality posts and articles so i suppose im lucky to have found this! I hope you will be adding more in the future...인계동호빠
http://www.0956798.xyz
http://www.0956799.xyz
http://www.0956800.xyz
http://www.0956801.xyz
http://www.0956802.xyz
http://www.0956804.xyz
http://www.0956805.xyz
http://www.0956936.xyz
http://www.0956938.xyz
http://www.0956939.xyz
http://www.0956942.xyz
http://www.0956943.xyz
http://www.0956944.xyz
http://www.0956945.xyz
http://www.0956947.xyz
http://www.0956948.xyz
http://www.0956949.xyz
http://www.0956950.xyz
http://www.0956951.xyz
http://www.0956952.xyz
http://www.0956953.xyz
http://www.0956963.xyz
http://www.0956964.xyz
http://www.0956965.xyz
http://www.0956966.xyz
http://www.0956967.xyz
http://www.0956968.xyz
http://www.0956969.xyz
http://www.0956970.xyz
http://www.0956972.xyz
http://www.0956973.xyz
http://www.0956974.xyz
http://www.0956975.xyz
http://www.0956976.xyz
http://www.0956977.xyz
http://www.0956978.xyz
http://www.0956979.xyz
http://www.0956980.xyz
http://www.0956981.xyz
http://www.0956982.xyz
http://www.0957176.xyz
http://www.0957177.xyz
http://www.0957178.xyz
http://www.0957179.xyz
http://www.0957180.xyz
http://www.0957181.xyz
http://www.0957182.xyz
http://www.0957183.xyz
http://www.0957184.xyz
http://www.0957185.xyz
http://www.0957186.xyz
http://www.0957187.xyz
http://www.0957188.xyz
http://www.0957189.xyz
http://www.0957190.xyz
http://www.0957191.xyz
http://www.0957192.xyz
http://www.0957193.xyz
http://www.0957194.xyz
http://www.0957195.xyz
http://www.0957196.xyz
http://www.0957197.xyz
http://www.0957198.xyz
http://www.0957199.xyz
http://www.0957200.xyz
http://www.0957201.xyz
http://www.0957202.xyz
http://www.0957203.xyz
http://www.0957204.xyz
http://www.0957205.xyz
http://www.0957206.xyz
http://www.0957208.xyz
http://www.0957209.xyz
http://www.0957210.xyz
http://www.0957211.xyz
http://www.0957214.xyz
http://www.0957215.xyz
http://www.0957216.xyz
http://www.0957217.xyz
http://www.0957218.xyz
http://www.0957219.xyz
http://www.0957220.xyz
http://www.0957221.xyz
http://www.0957222.xyz
http://www.0957223.xyz
http://www.0957224.xyz
http://www.0957225.xyz
http://www.0957226.xyz
http://www.0957227.xyz
http://www.0957228.xyz
http://www.0957229.xyz
http://www.0957230.xyz
http://www.0957232.xyz
http://www.0957234.xyz
http://www.0957235.xyz
http://www.0957236.xyz
http://www.0957237.xyz
http://www.0957238.xyz
http://www.0957239.xyz
http://www.0957240.xyz
http://www.0957241.xyz
http://www.0957242.xyz
http://www.0957243.xyz
http://www.0957244.xyz
http://www.0957245.xyz
http://www.0957246.xyz
http://www.0957247.xyz
http://www.0957248.xyz
http://www.0957249.xyz
http://www.0957250.xyz
http://www.0957251.xyz
http://www.0957253.xyz
http://www.0957254.xyz
http://www.0957255.xyz
http://www.0957256.xyz
http://www.0957257.xyz
http://www.0957259.xyz
http://www.0957260.xyz
http://www.0957261.xyz
http://www.0957262.xyz
http://www.0957263.xyz
http://www.0957264.xyz
http://www.0957265.xyz
http://www.0957267.xyz
http://www.0957268.xyz
http://www.0957269.xyz
http://www.0957270.xyz
http://www.0957271.xyz
http://www.0957272.xyz
http://www.0957273.xyz
http://www.0957274.xyz
http://www.0957275.xyz
http://www.0957276.xyz
http://www.0957278.xyz
http://www.0957279.xyz
http://www.0957280.xyz
http://www.0957281.xyz
http://www.0957282.xyz
http://www.0957283.xyz
http://www.0957284.xyz
http://www.0957285.xyz
http://www.0957286.xyz
http://www.0957287.xyz
http://www.0957288.xyz
http://www.0957289.xyz
http://www.0957290.xyz
http://www.0957291.xyz
http://www.0957293.xyz
http://www.0957294.xyz
http://www.0957295.xyz
http://www.0957296.xyz
http://www.0957297.xyz
http://www.0957298.xyz
http://www.0957299.xyz
http://www.0957300.xyz
http://www.0957301.xyz
http://www.0957302.xyz
http://www.0957303.xyz
http://www.0957305.xyz
http://www.0957307.xyz
http://www.0957308.xyz
http://www.0957309.xyz
http://www.0957310.xyz
http://www.0957311.xyz
http://www.0957312.xyz
http://www.0957313.xyz
http://www.0957314.xyz
http://www.0957315.xyz
http://www.0957316.xyz
http://www.0957317.xyz
http://www.0957318.xyz
http://www.0957319.xyz
http://www.0957320.xyz
http://www.0957321.xyz
http://www.0957322.xyz
http://www.0957323.xyz
http://www.0957324.xyz
http://www.0957325.xyz
http://www.0957326.xyz
http://www.0957327.xyz
http://www.0957328.xyz
http://www.0957329.xyz
http://www.0957330.xyz
http://www.0957331.xyz
http://www.0957332.xyz
http://www.0957338.xyz
http://www.0957339.xyz
http://www.0957340.xyz
http://www.0957341.xyz
http://www.0957342.xyz
http://www.0957343.xyz
http://www.0957344.xyz
http://www.0957345.xyz
http://www.0957346.xyz
http://www.0957347.xyz
http://www.0957348.xyz
http://www.0957349.xyz
http://www.0957350.xyz
http://www.0957351.xyz
http://www.0957352.xyz
http://www.0957353.xyz
http://www.0957354.xyz
http://www.0957355.xyz
http://www.0957356.xyz
http://www.0957357.xyz
http://www.0957358.xyz
http://www.0957359.xyz
http://www.0957360.xyz
http://www.0957361.xyz
http://www.0957362.xyz
http://www.0957363.xyz
http://www.0957364.xyz
http://www.0957365.xyz
http://www.0957366.xyz
http://www.0957367.xyz
http://www.0957368.xyz
http://www.0957369.xyz
http://www.0957370.xyz
http://www.0957371.xyz
http://www.0957372.xyz
http://www.0957373.xyz
http://www.0957374.xyz
http://www.0957376.xyz
http://www.0957377.xyz
http://www.0957378.xyz
http://www.0957379.xyz
http://www.0957380.xyz
http://www.0957381.xyz
http://www.0957382.xyz
http://www.0957383.xyz
http://www.0957384.xyz
http://www.0957385.xyz
http://www.0957386.xyz
http://www.0957387.xyz
http://www.0957388.xyz
http://www.0957389.xyz
http://www.0957390.xyz
http://www.0957391.xyz
http://www.0957392.xyz
http://www.0957393.xyz
http://www.0957394.xyz
http://www.0957395.xyz
http://www.0957396.xyz
http://www.111g1u.top
http://www.1125297.xyz
http://www.12345683.xyz
http://www.12345754.xyz
http://www.12345760.xyz
http://www.12345761.xyz
http://www.1956959.xyz
http://www.28mmp.top
http://www.39kesc.top
http://www.3ay289t.top
http://www.3jcxu4n.top
http://www.45mwkfp.top
http://www.4e67m9l.top
http://www.58gc.space
http://www.68gtsqo.top
http://www.6ouz339h.top
http://www.6t9t6bgw.top
http://www.737came9g.top
http://www.788ure.top
http://www.7hnvxz.top
http://www.81xqjpl.top
http://www.82wnwls.top
http://www.83awj.top
http://www.8f94xxl.top
http://www.8km1owi.top
http://www.8mbrzyn.top
http://www.8vepego.top
http://www.97kj6hc.top
http://www.990d7sqir.top
http://www.9lpzvnk.top
http://www.9psscjp.top
http://www.9z8wf0sn.top
http://www.adamsilverbillwalton.shop
http://www.apkhere.online
http://www.avodart.online
http://www.b52taixiu.online
http://www.bandarrdewi.site
http://www.biuacg.fun
http://www.bnqddzf.top
http://www.bocoranqq303.online
http://www.burabaitsbs.site
http://www.c88.site
http://www.call-boyjobs.online
http://www.cddnc8x.top
http://www.chengdudingxinrun.top
http://www.chikishevvladimir.site
http://www.classifiedweb.online
http://www.crowltheselinks.top
http://www.crowltheselinksnow.top
http://www.customsplat.com
http://www.daiki.site
http://www.dexfutop.top
http://www.dexi888.top
http://www.dlbpjyg.top
http://www.dxp1739.top
http://www.essaytogethersomalia.online
http://www.essaytogetherum.online
http://www.etheogen.online
http://www.filter9.top
http://www.freedragon.site
http://www.gamingtools.site
http://www.giaydantuongsunhouse.online
http://www.goletera.top
http://www.googlefastindex.top
http://www.googleindexthesedomains.top
http://www.googleindexthisdomain.top
http://www.hami666.top
http://www.herearethevalues.top
http://www.hereisthevalues.top
http://www.hkqtqjc.top
http://www.hnsymy8.top
http://www.hrfbtjrr.top
http://www.htfe.site
http://www.huozi1.top
http://www.ikansar.shop
http://www.increaseseo.site
http://www.itpro0.top
http://www.jeckmer.shop
http://www.jgssc58.top
http://www.kjpcpsl.top
http://www.km8qr83.top
http://www.l65uo.top
http://www.lebanoneyes.online
http://www.lktsh73.top
http://www.load888.top
http://www.lpmvqof.top
http://www.lqngoe.top
http://www.lucentspace.site
http://www.lvbdhl.top
http://www.meecase.top
http://www.minregion.online
http://www.movies123free.top
http://www.nogzufx.top
http://www.noleggio-auto.online
http://www.oaaccba.top
http://www.pljoogt.top
http://www.promaxinv.online
http://www.prrhhwc.top
http://www.pwxxx12.top
http://www.qkpch75.top
http://www.qlhxdcl.top
http://www.read666.top
http://www.reke.online
http://www.rjjdfqt.top
http://www.rkqddwz.top
http://www.rxqtgpl.top
http://www.saastemp.online
http://www.sacloud.online
http://www.samatv.top
http://www.sanderlei.online
http://www.sfmjtor.top
http://www.sifvnuf.top
http://www.sltnbnz.top
http://www.smartworld1dxp.site
http://www.ssc8m93.top
http://www.subvalueshare.top
http://www.suhaochen.top
http://www.tbblpr.top
http://www.tezizone.online
http://www.thisisthebest.top
http://www.tiengruoi.online
http://www.travelwithusa.top
http://www.travelwithusam.top
http://www.twittervideodownloader.online
http://www.uglbjgu.top
http://www.universaltruth.top
http://www.unniversaltruth.top
http://www.vattaro.shop
http://www.viagraprices.top
http://www.votre.space
http://www.w8eh0a.top
http://www.w9wwxk9.top
http://www.want888.top
http://www.websiteranking.online
http://www.wqzzzsl.top
http://www.wso55.online
http://www.wymvcxw.top
http://www.xdwwjms.top
http://www.xirkiuf.top
http://www.xupptop.top
http://www.yiyecao2.top
http://www.yrqqnws.top
http://www.yv7u0n.top
http://www.yx889.top
http://www.yznavai.online
http://www.zjpchzi.top
http://www.aiofunnel.online
http://www.asmonacojersey.online
http://www.atmdomino.online
http://www.bluelinecourierservices.online
http://www.ccblackloadgame.online
http://www.cccartoongame.online
http://www.ccdddgames.online
http://www.ccfianalgame.online
http://www.ccgameanime.online
http://www.ccgamebkk.online
http://www.ccgamedee.online
http://www.ccgamedong.online
http://www.ccgameonlinestation.online
http://www.ccgamestudio.online
http://www.ccgoodgamestation.online
http://www.ccigggame.online
http://www.ccjingjunggame.online
http://www.cckurugamestudio.online
http://www.divinemu.online
http://www.eatpraynurse.online
http://www.ehyderabad.online
http://www.harrytarrantarena.online
http://www.informaticoadomicilio.online
http://www.kevinsnow.online
http://www.kinorupka.online
http://www.lakedoorlogistic.online
http://www.lowiekesfilmfestijn.online
http://www.model-facturi.online
http://www.nhaphotakarabinhbuong.online
http://www.noithatviet.online
http://www.profesionalpro.online
http://www.rcktl.online
http://www.stopncov.online
http://www.sysli.online
http://www.theozonegym.online
http://www.topxhamster.online
http://www.uniquesystems.online
http://www.viagranrx.online
http://www.wapenbroeders-limburg.online
http://www.amwreoth.online
http://www.androidfilmy.online
http://www.androidgps.online
http://www.apartemenjogja.online
http://www.bcbgshop.online
http://www.blessmecreations.online
http://www.brandonlee.online
http://www.careerinfosolutions.online
http://www.careheroes.online
http://www.danitaeke.online
http://www.dazzling-eg.online
http://www.descargalos.online
http://www.dimulcompu.online
http://www.discontinue.online
http://www.downloadfreeprograms.online
http://www.entreirmaos.online
http://www.fimdornascostas.online
http://www.firmabak.online
http://www.fixagencia.online
http://www.fndcars.online
http://www.formuladeatracao.online
http://www.ganjaliveseeds.online
http://www.garmingpshelp.online
http://www.gitraqr.online
http://www.globalfxindex.online
http://www.govtschooljalalsar.online
http://www.halitoglugrup.online
http://www.hdgid.online
http://www.hindisongshub.online
http://www.htibleiden.online
http://www.jamilahmed.online
http://www.jasaceme.online
http://www.kingfilmkis.online
http://www.kinolord-hd.online
http://www.korfbalradio.online
http://www.leenaartscoaching.online
http://www.lorentzapotheek.online
http://www.madesigner.online
http://www.mariusblikslager.online
http://www.mevabesausinh.online
http://www.msantiago.online
http://www.mytrusted.online
http://www.najonchemicals.online
http://www.neemnugitaarles.online
http://www.ninasmikyim.online
http://www.offerstyle.online
http://www.oficialcosmeticosartesanais.online
http://www.opstandingskerk-enschede.online
http://www.patricklewsymptom.online
http://www.peerblog.online
http://www.pokemonfun.online
http://www.prinsessenjurkenshop.online
http://www.qisatkifah.online
http://www.resolvimudar.online
http://www.restontoday.online
http://www.sanatate-viata.online
http://www.sobhaayanaproperty.online
http://www.sobhaayanaresidenceproject.online
http://www.sobhaayanaresidency.online
http://www.srdcwl.online
http://www.srrcwl.online
http://www.szkolanr1.online
http://www.tagomall.online
http://www.teambutler.online
http://www.tesprediksi.online
http://www.theapkpure.online
http://www.thegatget2.online
http://www.thepeacockgarden.online
http://www.tjeerdbroekhuizen.online
http://www.ueber-mich.online
http://www.urpiweb.online
http://www.vergaderingsouburg.online
http://www.vogelverenigingens.online
http://www.vrijetijdsidee.online
http://www.wedinvi.online
http://www.wellthought.online
http://www.werkveldcoaching.online
http://www.westerpaviljoen-rotterdam.online
http://www.whiplash-reflex.online
http://www.ytgy.online
http://www.zezijnterug.online
http://www.zwgdh.online
I recently came across your blog and have been reading along. I thought I would leave my first comment. I don’t know what to say except that I have enjoyed reading. 소액 현금화








i read a lot of stuff and i found that the way of writing to clearifing that exactly want to say was very good so i am impressed and ilike to come again in future..http://wwscc.org/evinfo/pages/1xbet_promo_code_for_registration___sign_up_bonus_india.html