출처 : https://velog.io/@pyose95/Data-Analysis
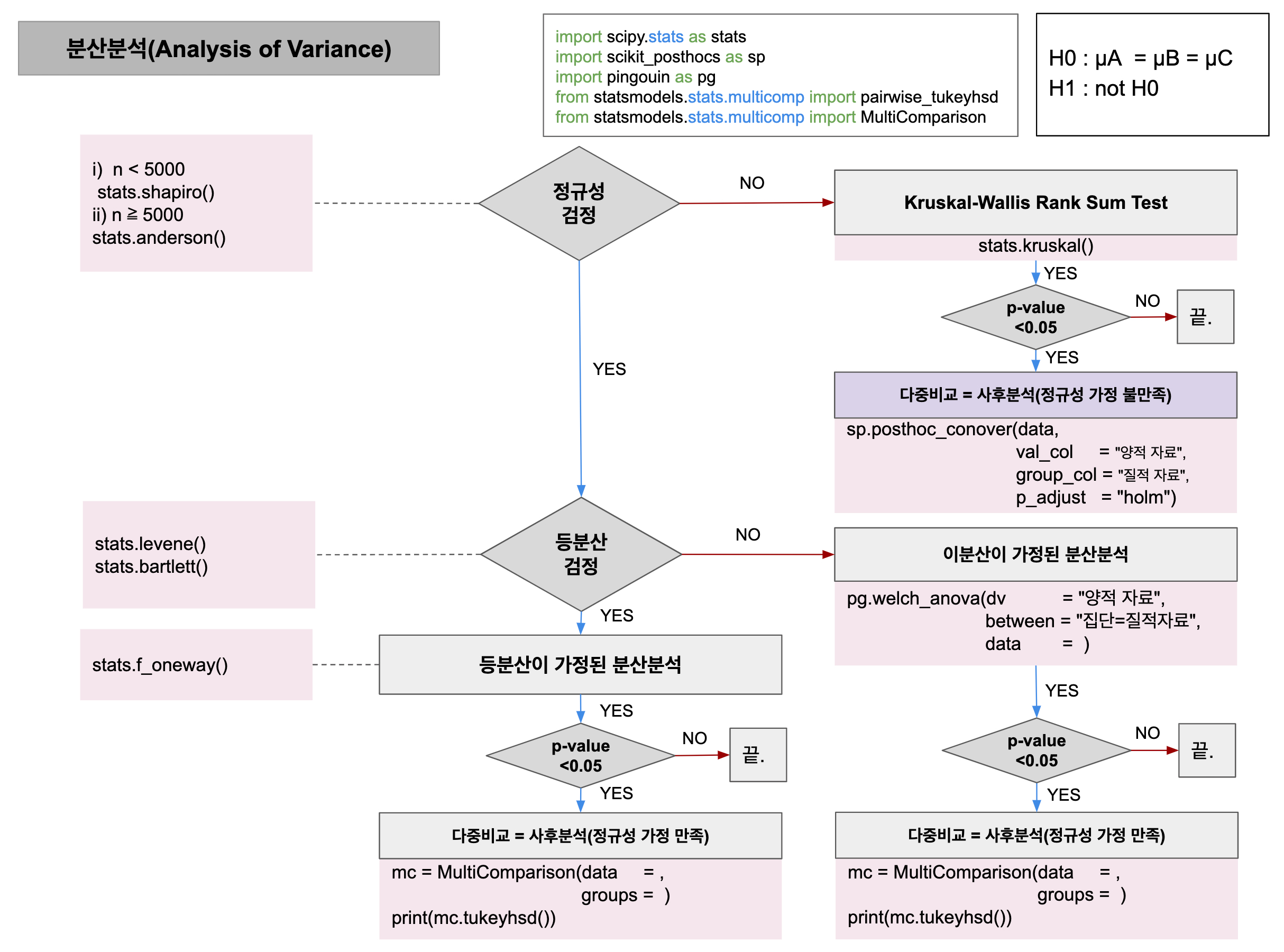
📌세 개 이상의 모집단에 대한 가설검정 – 분산분석(ANOVA, '변량분석'이라고도 한다.)
‘분산분석’이라는 용어는 분산이 발생한 과정을 분석하여 요인에 의한 분산과 요인을 통해 나누어진 각 집단 내의 분산으로 나누고 요인
에 의한 분산이 의미 있는 크기를 크기를 가지는지를 검정하는 것을 의미한다.
세 집단 이상의 평균비교에서는 독립인 두 집단의 평균 비교를 반복하여 실시할 경우에 제1종 오류가 증가하게 되어 문제가 발생한다.
이를 해결하기 위해 Fisher가 개발한 분산분석(ANOVA, ANalysis Of Variance)을 이용하게 된다.
- 독립변수: 범주형, 종속변수: 연속형
- F-value = 그룹 간 분산(variable between group) / 그룹 내 분산 (variable within group)
그룹간 분산이 크고, 그룹내 분산이 작을수록 좋다.
- F 분포 : 서로 다른 두 개 이상의 모집단의 분산이 같은지를 확인할 때 사용함
- 서로 독립인 세 집단의 평균 차이 검정 (일원 분산분석 : oneway anova)
측정값에 영향을 미치는 요인(독립변수)이 1개 : 1개의 요인에 대해 세 개 이상의 그룹의 평균차이 검정
집단 간 분산이 집단 내 분산보다 충분히 큰 것인가를 파악하는 것
- 일원 분산분석이 가장 많이 사용한다.
분산분석(ANOVA) 의 종류에 관련된 내용 사이트 참조
https://bioinformaticsandme.tistory.com/198
❓일원 분산분석, 실습 예제를 통해 알아보자!!
먼저 가설부터 설정해본다.
✍️가설
강남구에 있는 GS 편의점(요인 1개) 3개지역(집단) 알바생의 급여에 대한 평균에 차이가 있는지 검정
- 귀무 : 편의점(요인) 3개지역(집단) 알바생의 급여에 대한 평균에 차이가 없다.
- 대립 : 편의점(요인) 3개지역(집단) 알바생의 급여에 대한 평균에 차이가 있다.
✍️입력
# 필요한 라이브러리 추가
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# 준비되어있던 파일을 이용해 불러와 사용
data = pd.read_csv('../testdata/group3.txt', header=None)
data.columns=['pay', 'shop']
print(data)💻출력
pay shop
0 243 1
1 251 1
2 275 1
3 291 1
4 347 1
5 354 1
6 380 1
7 392 1
8 206 2
9 210 2
10 226 2
11 249 2
12 255 2
13 273 2
14 285 2
15 295 2
16 309 2
17 241 3
18 258 3
19 270 3
20 293 3
21 328 3✍️그룹을 1,2,3 그룹으로 나누고 정규성 확인(shapiro)
# 각 편의점(1,2,3)마다 급여 추출
gr1 = data.loc[data['shop']==1, 'pay']
gr2 = data.loc[data['shop']==2, 'pay']
gr3 = data.loc[data['shop']==3, 'pay']
# 각 편의점의 급여 평균 확인
print(np.mean(gr1))
>> 316.625
print(np.mean(gr2))
>> 256.44444444444446
print(np.mean(gr3))
>> 278.0
# scipy.stats.shapiro() 을 사용하여 정규성 만족 확인
print(stats.shapiro(gr1).pvalue)
>> 0.33368444442749023 > 0.05 : 정규성 만족
print(stats.shapiro(gr2).pvalue)
>> 0.6561092138290405 > 0.05 : 정규성 만족
print(stats.shapiro(gr3).pvalue)
>> 0.832481324672699 > 0.05 : 정규성 만족❗만약 여기서 정규성 만족을 못했다면 Kruskal-Wallis H-검정 테스트 진행
scipy.stats.kruskal(*samples, nan_policy='propagate', axis=0, keepdims=False)
# 정규성 만족 못했을 경우 kruskal() 로 검정 테스트 진행
print(stats.kruskal(gr1, gr2, gr3))
>> KruskalResult(statistic=4.18524374176549, pvalue=0.12336326887166982)위에 정규성 검정을 만족했으니 등분산성 검정을 진행해야한다.
보통 levene 나 bartlett 을 사용한다.
# 등분산성 검정 진행
print(stats.levene(gr1, gr2, gr3).pvalue)
>> 0.045846812634186246
# 0.05 보다 작아 불만족이긴 하나 이정도는 만족으로 봐도 무난하다.
print(stats.bartlett(gr1, gr2, gr3).pvalue)
>> 0.3508032640105436
# 등분산성 만족❗등분산성 만족하지 못했을 경우 welch's anova 검정 사용
from pingouin import welch_anova
# dv = 종속변수, between = 독립변수
print(welch_anova(data=data, dv='pay', between='shop'))
'''
Source ddof1 ddof2 F p-unc np2
0 shop 2 11.064588 2.970386 0.092767 0.280921
p-unc 값이 p-value 이다.
여기서 p-value 는 0.092767 > 0.05 이므로 귀무 채택된다.
편의점(요인) 3개지역(집단) 알바생의 급여에 대한 평균에 차이가 없다.
'''📖일원분산분석
정규성과 등분산성 모두 만족할 경우 일원분산분석 ANOVA 검정을 진행한다.
일원 분산 분석에는 2가지 방법이 있다.
📝일원분산분석 방법1) : anova_lm()
DataFrame형의 데이터를 사용
범주형 데이터를 사용하는 독립변수 앞에는 C를 붙여줘야 한다.
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# 종속변수 ~ C(독립변수)
lmodel = ols('pay ~ C(shop)', data=data).fit()
print(anova_lm(lmodel, typ=1))
'''
df sum_sq mean_sq F PR(>F)
C(shop) 2.0 15515.766414 7757.883207 3.711336 0.043589
Residual 19.0 39716.097222 2090.320906 NaN NaN
* 여기서 PR(>F) 값이 p-value 이다.
p-value(0.043589) < 0.05 이므로 귀무기각이다.
편의점(요인) 3개지역(집단) 알바생의 급여에 대한 평균에 차이가 있다.
'''📝일원분산분석 방법2) : f_oneway()
f_statistic, pvalue = stats.f_oneway(gr1, gr2, gr3)
print('f_statistic:{}, pvalue:{}'.format(f_statistic, pvalue))
'''
f_statistic:3.7113359882669763, pvalue:0.043589334959178244
p-value(0.043589) < 0.05 이므로 귀무기각이다.
편의점(요인) 3개지역(집단) 알바생의 급여에 대한 평균에 차이가 있다.
'''📝분산분석(ANOVA)이 끝난 후에는 이대로 끝난 것이 아니라 어떻게 차이가 나는지? 얼마나 차이가 나는지 확인을 해야하는데 이것을 '사후검정' 이라한다.
사후검정에는 여러가지 종류가 있고 각 종류마다 특징들이 있다.
분석가 판단 하에 올바른 사후검정을 선택해야 하며 여기서는 Tukey 사후검정을 해보겠다.
📖사후검정 Tukey
# Tukey 라이브러리 가져오기
from statsmodels.stats.multicomp import pairwise_tukeyhsd
# endog = 종속변수, groups = 독립변수
tukey_result = pairwise_tukeyhsd(endog=data['pay'], groups=data['shop'])
print(tukey_result)💻 출력결과
Multiple Comparison of Means - Tukey HSD, FWER=0.05
======================================================
group1 group2 meandiff p-adj lower upper reject
------------------------------------------------------
1 2 -60.1806 0.0355 -116.619 -3.7421 True
1 3 -38.625 0.3215 -104.8404 27.5904 False
2 3 21.5556 0.6802 -43.2295 86.3406 False
------------------------------------------------------
* 여기에서 reject 값이 True 일 경우 차이가 있다는 의미이고, False 는 차이가 없다는 의미이다.