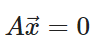※ 시각화와 이해의 편의를 도모하기 위해 벡터와 행렬이 정의되는 체(field)는 실수(real number)로 한정함.
Prerequisites
- 벡터의 기본 연산 (상수배, 덧셈)
- 행렬 곱에 대한 또 다른 시각
- 행렬과 선형 변환
행렬은 선형변환이다

함수(function)의 가장 근본적인 정의

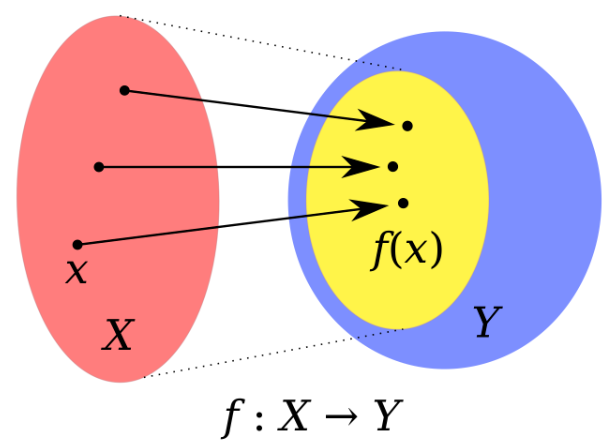
부분공간(subspace)이란?
벡터 공간은 기본적으로 벡터를 원소로 하는 집합(set)이다.
부분 공간이라는 것은 부분 집합의 개념을 벡터 공간에 접목시킨 것으로 볼 수 있다.
즉, 집합에서 부분 집합이 있는 것 처럼 벡터 공간에서도 벡터 공간의 기본 구조를 그대로 유지하는 작은 벡터 공간, 즉 부분 공간이 있다.
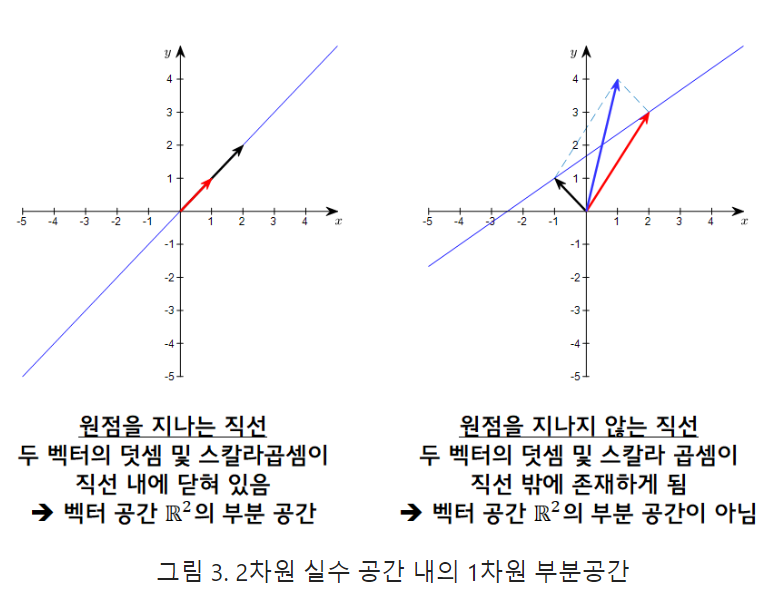
가령, 2차원 실수 공간에서 부분 공간을 하나 생각해보자면 원점을 지나는 직선 상에 있는 모든 벡터들의 집합은 1차원 부분 공간을 이룬다.
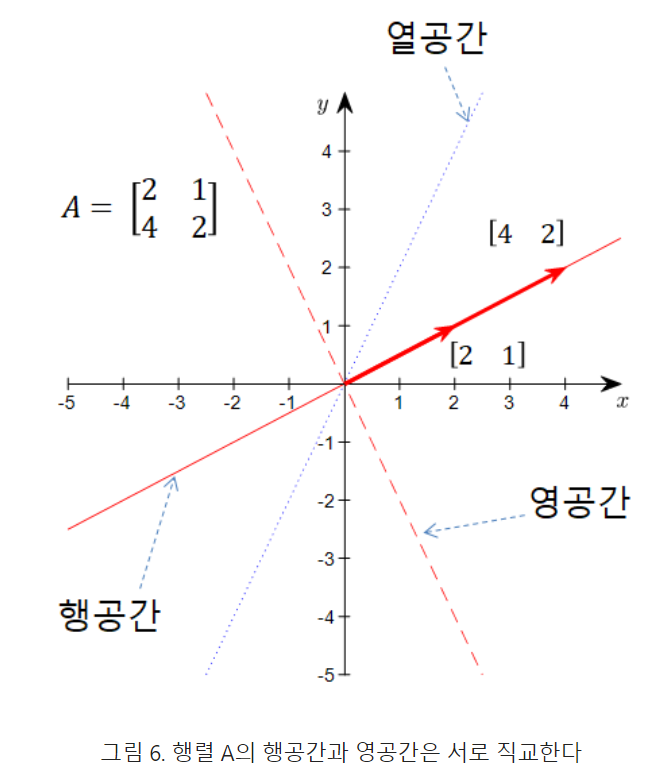
행공간과 열공간
이런 관점에서 보았을 때, 우리에게 주어진 임의의 행렬
A
의 모든 행 혹은 모든 열들의 선형결합으로 구성된(즉, span) 벡터공간은 부분 공간이며 각각을 행공간(row space), 열공간(column space)이라고 부른다.
예를 들어 행렬 A가 아래와 같이 주어져있다고 해보자.
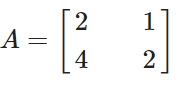
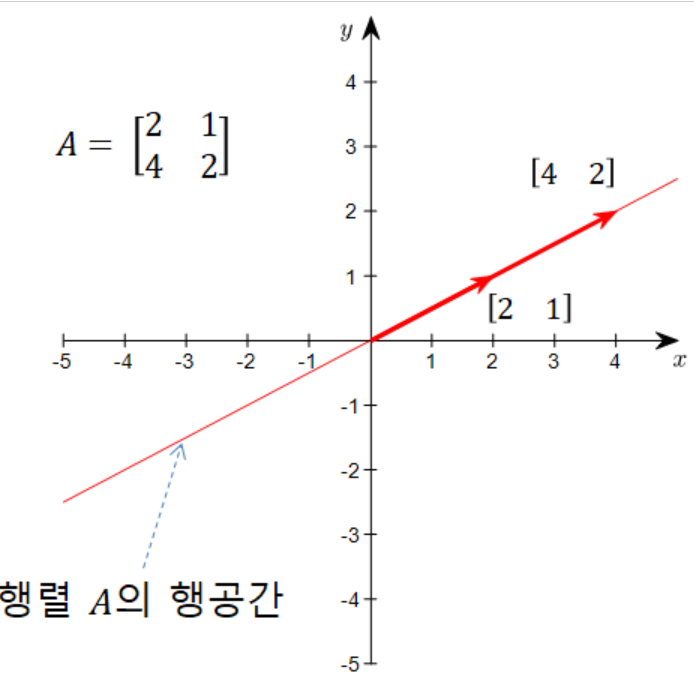
그러면, 행공간은 벡터
[2 1]와 [4 2]의 선형 결합으로 이루어진 선 상에 있는 모든 벡터들의 집합이다
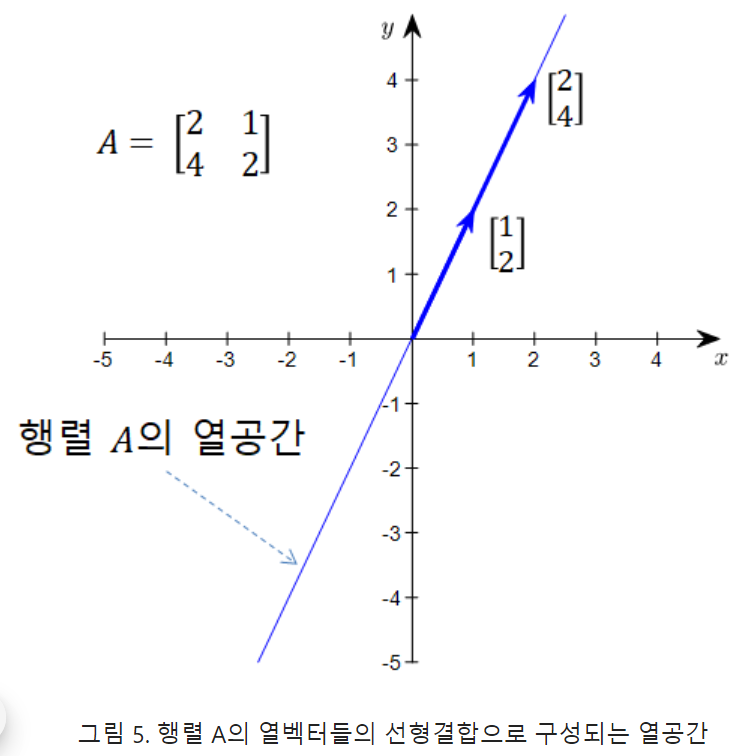
또, 열공간은 벡터
[2 4]T와 [1 2]T의 선형 결합으로 이루어진 선 상에 있는 모든 벡터들의 집합이다.
영공간(null space)
행렬 A에서 즉각적으로 인지하긴 어렵지만 영공간(null space)라는 부분 공간도 존재한다.
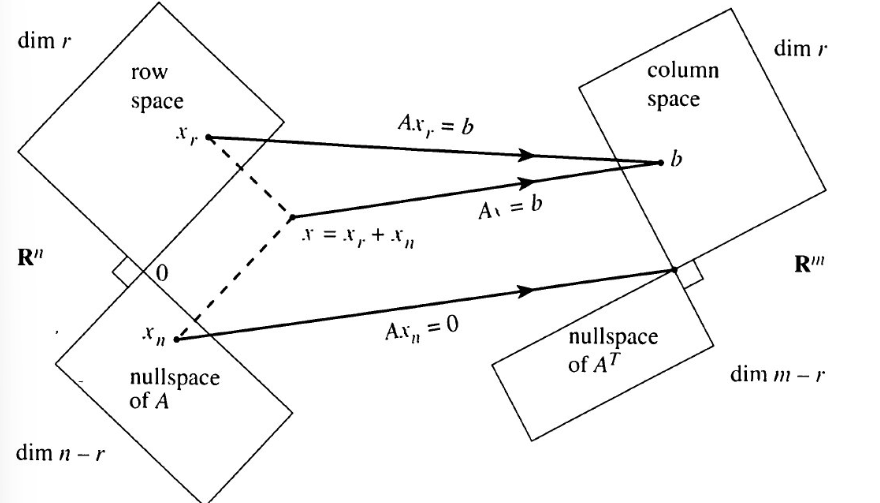
영공간은 아래와 같은 조건을 만족하는
→
x 들의 집합이다.
즉, A라는 선형 변환 후에 모두 0을 출력하게 만들어주는 입력 벡터 x들인 것이다.