LinearAlgebra
1.[선형대수] 스칼라, 벡터, 행렬
해를 찾을 때, Augmented MatrixReduced Echelon FormEchelon FormEigenvalue, EigenvectorEigenproblem, Generalized Eigenproblem
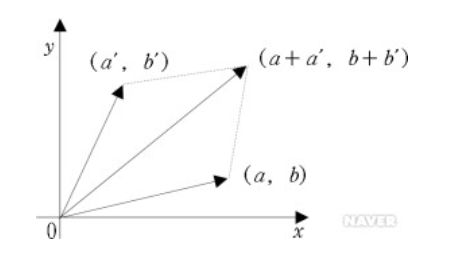
2.[선형대수] 벡터공간 및 부분공간

왜 a, b, c 벡터가 다 원점을 시작점으로 하는가? a, b,c 벡터가 (0,0,0)을 관통하는 직선상에 놓인 세 점ㅇ
3.[선형대수] 여러 행렬 정리
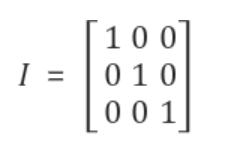
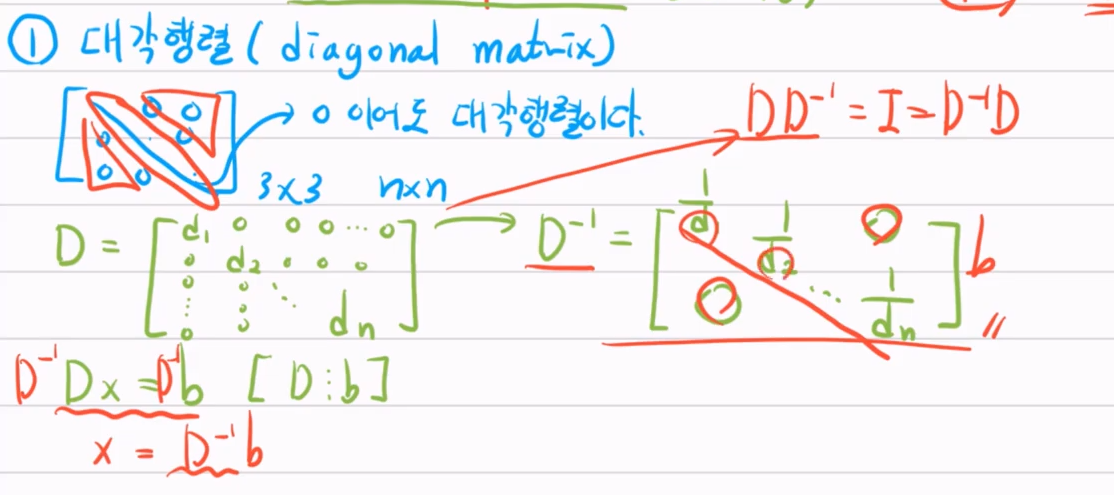
행렬의 대각 원소(Diagonal Component)는 모두 1, 대각 원소가 아닌 원소들은 모두 0으로 이루어진 행렬이때 A-1은 1/A가 아님.기존 행렬의 행의 순서를 교체(치환)해주는 행렬\-> i번째 행과 j번째 행의 순서를 바꿈을 의미함.치환행렬은 단위행렬(I
4.[선형대수] 일차종속 및 독립

정의 : 벡터 공간 V의 원소 v1,v2,v3...vn에 대하여 a1,a2,a3,...an이 임의의 실수일 때, a1v1+a2v2+a3v3+...anvn을 v1,v2,v3...vn의 일차 결합이라 한다. 일차결합으로 인한 최종 결과값(계산된 값) = 생성벡터공간 V의
5.[선형대수] 선형시스템 (선형방정식)
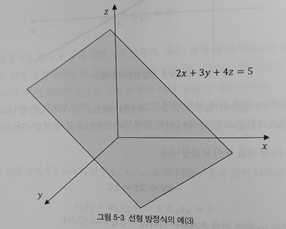
여러 개의 방정식이 주어졌을 때 연립 방정식으로 해(solution)을 수하는 방법을 배웠을 것이다. 행렬을 이용하면 연립방적식의 해를 쉽게 구할 수 있는데, 이때 연립 방정식은 다른 말로 선형 시스템이라고도 한다.본 페이지에서는 선형 방정식과 선형 시스템, 동차 선형
6.[선형대수] 행렬식

행렬식(determinant) = 행렬의 특성을 하나의 숫자로 표현하는 방법 중 하나.= 정사각행렬을 스칼라로 변환하는 함수ex) 행렬식의 절댓값은 해당 행렬이 단위 공간을 얼마나 늘렸는지 혹은 줄였는지를 의미함. 따라서 행렬식의 절댓값이 1이라면 해당 행렬이 단위
7.[선형대수] 기저와 랭크

벡터 공간을 생성하는 선형 독립인 벡터들.기저는 유일하지 않다.(1,0), (0,1)도 기저가 될 수 있으며 (10,0). (0,20)도 기저가 될 수 있다. {s1,s2,s3,,,sn}이 공간 sfmf todtjdgksek.s1,s2,s3,,,sn은 선형 독립(lin
8.[선형대수] 랭크
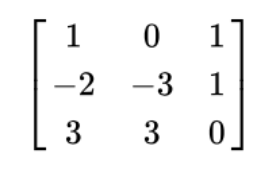
행렬의 랭크는 행렬이 나타낼 수 있는 벡터 공간에서 기저의 개수를 의미하고, 이 기저는 서로 독립인 행또는 열의 벡터의 개수에 의해서 결정된다. 열과 행의 랭크는 서로 같은 값을 가지므로, 행렬의 랭크를 구할 때에는 한쪽의 랭크만 계산하면 되고, 서로 선형 독립인 벡터
9.[선형대수] Gauss Jordan Elimination, Gauss Elimination

가우스 행렬을 이용해 방정식의 해를 구하는 방법 = 가우스 소거법 기약 가우스 행렬을 이용해 방정식의 해를 구하는 방법 = 가우스 조르단 소거법
10.[선형대수] 4개 주요 부분 공간의 관계
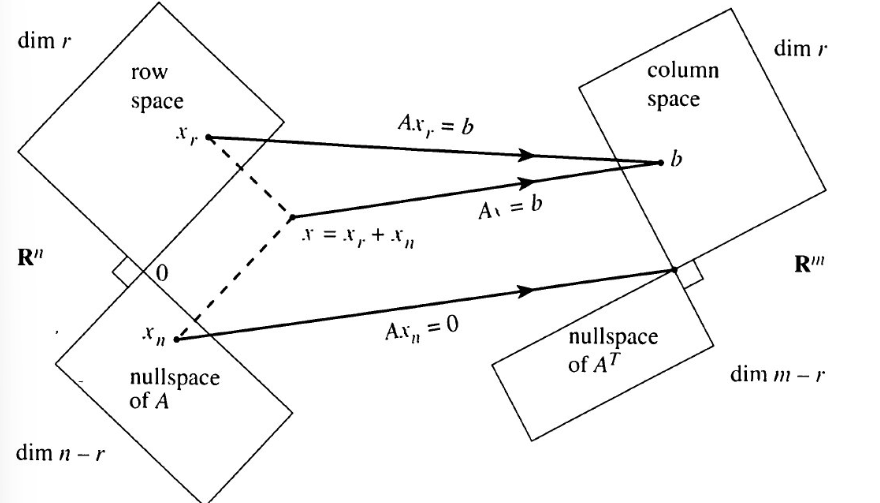
※ 시각화와 이해의 편의를 도모하기 위해 벡터와 행렬이 정의되는 체(field)는 실수(real number)로 한정함.벡터의 기본 연산 (상수배, 덧셈)행렬 곱에 대한 또 다른 시각행렬과 선형 변환벡터 공간은 기본적으로 벡터를 원소로 하는 집합(set)이다.부분 공간
11.[선형대수] 기저의 변환
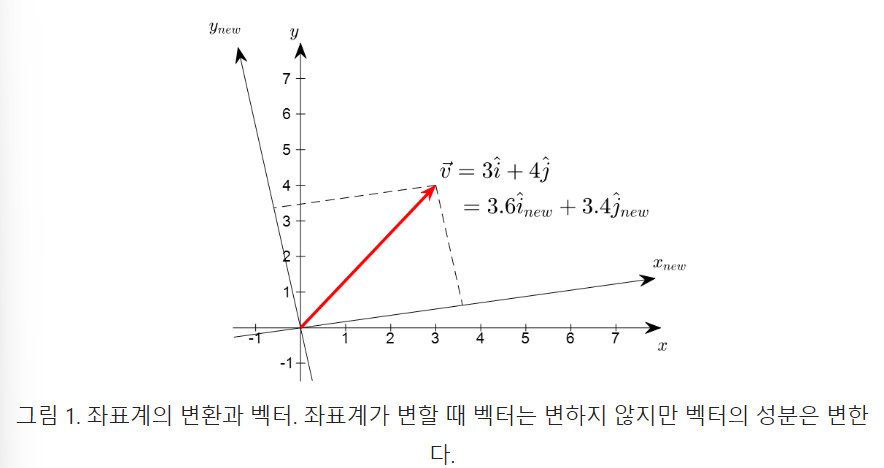
좌표계가 변하더라도 빨간색으로 표시한 화살표는 요지부동(불변성)이다. 하지만, 동시에 다른 좌표계를 통해 본 벡터의 좌표는 (3, 4)에서 (3.6, 3.4)로 바뀐 것(가변성)을 볼 수 있다.좌표평면 상의 어떤 점(즉 벡터)을 표현할 때 우리가 보통 사용하는 좌표계는
12.[선형대수] 행렬 곱
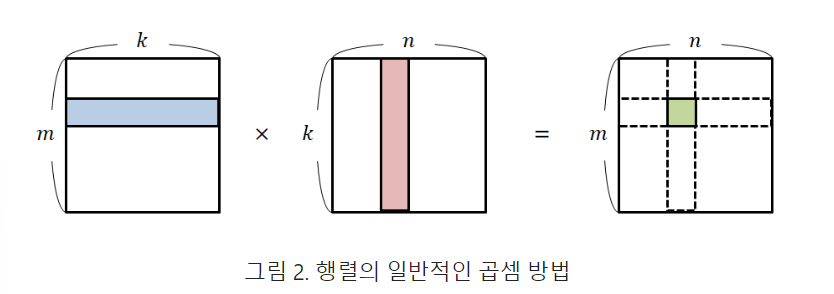
Math Processing Error이것을 잘 뜯어 생각해보면, 왼쪽에 있는 행렬에서 행 하나를 가져오고 오른쪽에 있는 행렬에서 열 하나를 가져와서 계산하게 된다는 것을 알 수 있다.행렬 곱이 이런 방식으로 정의되는 이유는 행렬이 일종의 함수라는 관점에서부터 얻어진다
13.[선형대수] 2. 행렬식_2

'행렬의 주대각 원소의 부호는 항상 +이고, +사이의 원소 부호는 -이다.한 행 또는 열을 선택 (무엇을 선택하든 계산결과값은 달라지지 않음)선택한 열 또는 행의 원소에 대하여 각 원소 1개에 대해 원소가 속하는 열과 행을 제외한 나머지 원소의 행렬식 값을 계산위 A
14.[선형대수] 역행렬

역행렬 역행렬 구하는 방법 adj(A)란 수반행렬이다. 1. 2. 3. 
# 미지수가 n개인 연립일차방정식의 근(해)과 계수(Rank)와의 관계 (2) 오직 하나 존재한다 = 유일한 해를 갖는다 (3) ~이외의 해를 갖는다. # 예제 1. 2. 
\-x+2y = 0과 2ㅌ-4ㅛ = 0 은 같은 식이므로, -x + 2y = 0 을 만족하는 수많은 x와 y 중 하나의 경우의 수만 제시하면 된다.
17.[선형대수] 기저 및 차원
기저를 통해 R2 안에서의 모든 벡터를 생성해낼 수 있다. 독립관계성을 갖는다.특정되어 있지 않다. 3과 같이 기저는 정해져있지 않지만, 기저의 기수는 변하지 않는다.(기저의 개수 = 차원)정리하면 다음과 같다.
18.[선형대수] 고유치 및 고유벡터의 성질

고유치 및 고유벡터의 성질 1 예제 1. 2. 3. 
"움직임"을 표현.방향과 크기만 같다면 두 벡터는 같음.크기가 1인 벡터.상대적이므로 자기자신의 길이로 나누어준다. 덧셈, 뺄셈좌표계에서 두 벡터의 덧셈과 뺄셈
20.[선형대수] 벡터의 내적

벡터의 내적 내적의 정의 내적의 성질 예제 
가역행렬을 갖는 (적당한) Q가 있을 때, 다음 수식을 만족하는 행렬 A와 B를 닮은 행렬이라고 한다.다음 A, Q, Q의 역행렬이 있을 때,A의 닮은 행렬 B는 다음과 같다.따라서, 고유치 1과 3에 따른 각각의 고유벡터는 다음과 같게 된다.
22.[선형대수] LU 분해 (LU decomposition) (1) 특수한 경우
Ref: https://www.youtube.com/watch?v=zM-NXfNsnCo&list=PLdEdazAwz5Q_n47tqf0QY94ASCmWqeGX1&index=31Ax=b에서 해집합 x를 효율적으로 구하기 위해 고안됨 (앨런 튜링).(기존의 방법:
23.선형대수] 대각행렬의 거듭제곱

참고) 귀납법의 사전적 의미추리/추론/논증의 방법 가운데 하나. 통칭 귀납법, 귀납 추론이라고도 한다. 연역논증과 함께 논리학의 두 축을 이루고 있다. 흔히 '구체적 사실로부터 보편적 사실을 추론해내는 방식'이라고 정의되지만, 이것은 귀납 논증의 일례만을 보여주는 것으
24.[선형대수] LU 분해 (LU decomposition) (2) 이론적인 근거들
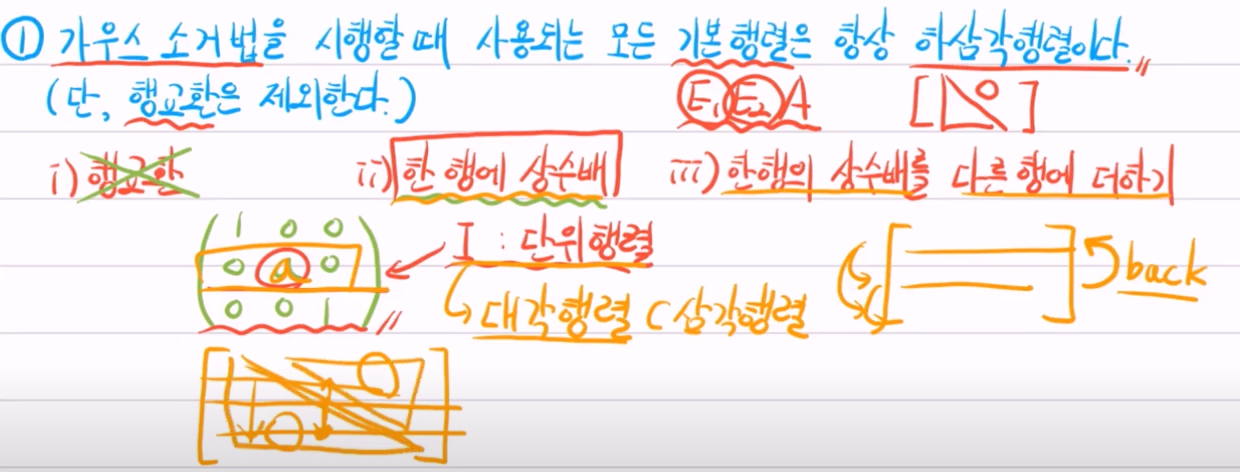
LU 분해
25.[선형대수] LU 분해 (LU decomposition) (3) 성질 및 계산법

LU.분해는 요청이 거듭해서 들어오더라도 빠르게 처리할 수 있음: 가우스소거법을 사용해서 E행렬을 거듭해서 곱해줌