Ref: https://www.youtube.com/watch?v=zM-NXfNsnCo&list=PLdEdazAwz5Q_n47tqf0QY94ASCmWqeGX1&index=31
[LU 분해]
Ax=b에서 해집합 x를 효율적으로 구하기 위해 고안됨 (앨런 튜링).
(기존의 방법: 가우스 조단 소거법)
특수 -> 확장 -> 일반화
특수한 경우
(1) 대각행렬 (diagonal matrix)
대각성분 제외 모두 0인 원소를 갖는 행렬 (대각성분이 0이 아니어도 상관없음)
주의: 대각성분 d1~dn 중 하나라도 0이면 D는 비가역행렬이다.
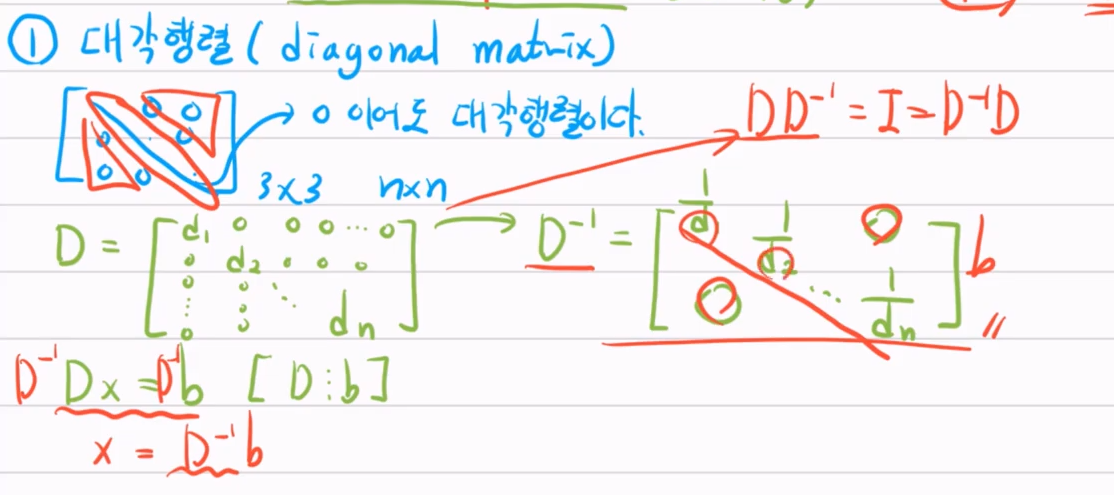
참고: 대각행렬의 성질
대각행렬을 거듭제곱한 결과는 단순히 대각행렬의 대각원소들을 거듭제곱해준 것과 같다.

(2) 삼각행렬 (triangular matrix)
대각원소를 기준으로 아래쪽만 또는 위쪽만 0인 원소를 갖는 행렬 (나머지 부분이 0이 아니어도 상관없음)

이 행렬에서 가우스 조단 소거법을 할 경우 (back = back substitution, forward = forward substitution)
LU 분해의 효율성

=> 행렬의 크기가 커질수록, 속도는 훨씬 빨라짐 (cpu에 따라서도 다르지만, 가우스보단 빠름)
결과적으로 일반적인 행렬 A를 LU로 바꿨을 때 걸리는 시간은 n의 세제곱 정도의 시간이 걸림
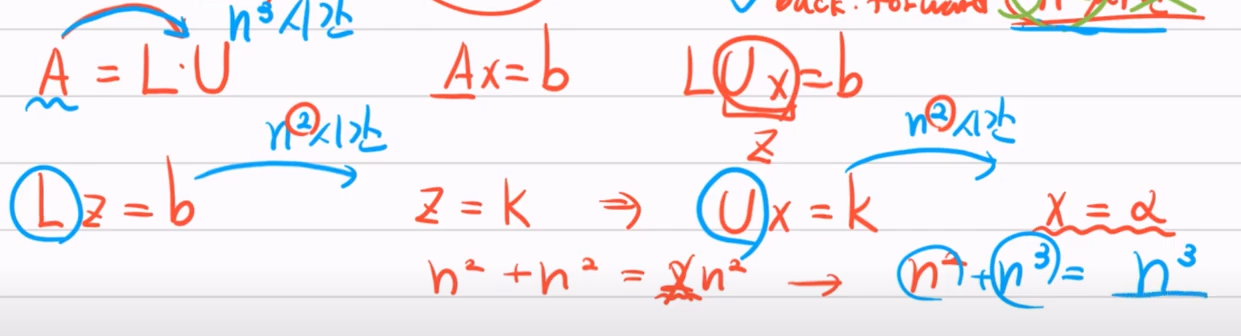
위와 같이 봤을 때는 가우스에 비해 훨씬 빠른 것 같진 않지만, A를 LU로 한번 분해하면 계속 분해할 필요는 없으므로 아래와 같이 방정식을 풀 때에 걸리는 시간 n의 제곱시간만 n번 (n2 x n) 소요됨
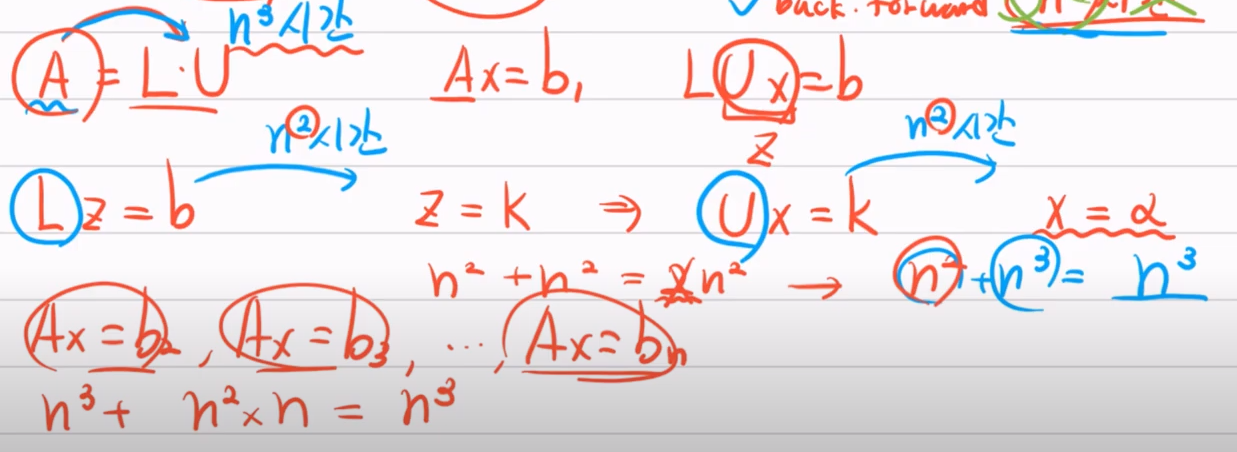
하지만 가우스 조단 소거법의 경우 A행렬을 분해할 때마다 n3의 시간이 n번 소요되므로 결과적으로 n의 네제곱의 시간이 걸리므로 back subsitution, forward substitution 즉 LU분해를 사용하는 것이 훨씬 효율적이다.