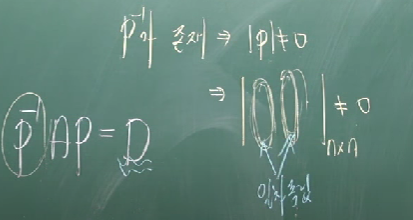닮은 행렬
가역행렬을 갖는 (적당한) Q가 있을 때, 다음 수식을 만족하는 행렬 A와 B를 닮은 행렬이라고 한다.
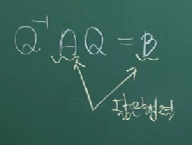
다음 A, Q, Q의 역행렬이 있을 때,
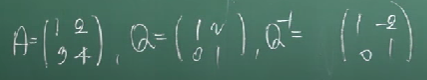
A의 닮은 행렬 B는 다음과 같다.
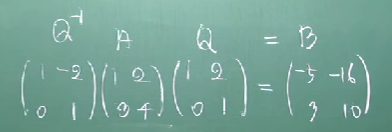
닮은 행렬의 성질
행렬의 대각화
P (대각화시키는 행렬) : A의 고유벡터로 이루어진 행렬
D (대각화 행렬) : A의 고유치로 이루어진 행렬
1. A의 고유치를 구한다.
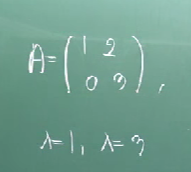
2. 고유치에 따른 고유벡터를 구한다.
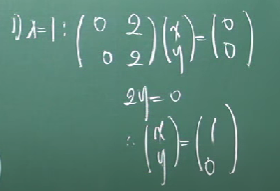
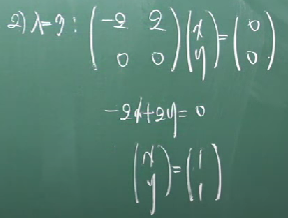
따라서, 고유치 1과 3에 따른 각각의 고유벡터는 다음과 같게 된다.
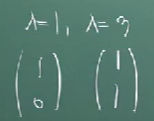
3. A의 고유벡터로 이루어진 P를 구한다.
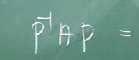
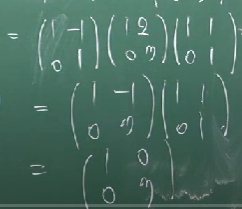
대각화 행렬의 성질
1. 행렬식(determinant)의 값이 같다.
2. trace(주대각원소) 합의 값이 같다.
3. Rank 값이 같다.
4. 고유치의 값이 같다.
예제
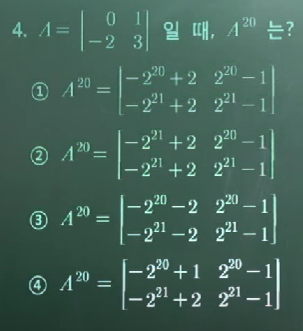
대각화 조건
nxn 정방행렬에서 행렬식의 값이 0이 아니려면 각 열이 서로 일차독립관계여야 한다.
= 일차독립인 고유벡터의 개수가 n개 존재해야 한다.
= 서로 다른 고유치가 n개 존재해야 한다.
veloger