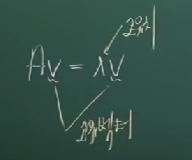
# 고유치 및 고유벡터의 정의
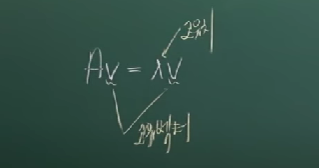
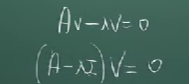
고유치 = 행렬식의 값이 0이 되게 하는 람다값
고유벡터 = 0이 아닌 벡터이고, 행렬식 값이 0이다. (역행렬이 존재하지 않음.)
만약, 역행렬이 존재한다면,
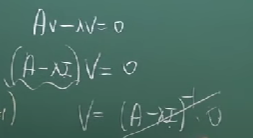
위의 식처럼 전개되고, V는 0이 되므로, 고유벡터는 역행렬이 존재하지 않는다.
고유방정식 = 행렬식의 값이 0이 되게 하는 방정식
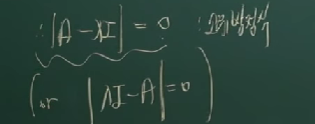
예제 1.
고로, 다음 예제에서 "고유 방정식"은
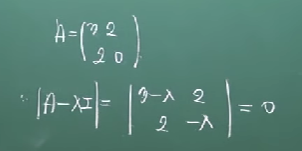
"고유치"는 아래와 같다.
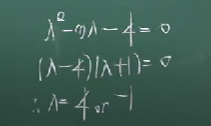
고유치는 4와 -1이 된다.
"고유벡터"는 아래 식을 만족하는 V이다.
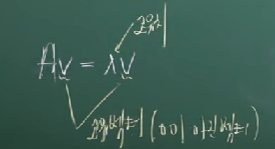
먼저, 고유치가 4일 때의 고유벡터는 아래와 같이 구한다.
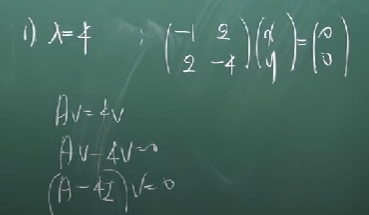
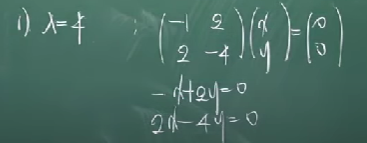
-x+2y = 0과 2x-4y = 0 은 같은 식이므로, -x + 2y = 0 을 만족하는 수많은 x와 y 중 하나의 경우의 수만 제시하면 된다.
두번째로, 고유치가 -1일 때의 고유벡터는 아래와 같이 구한다.
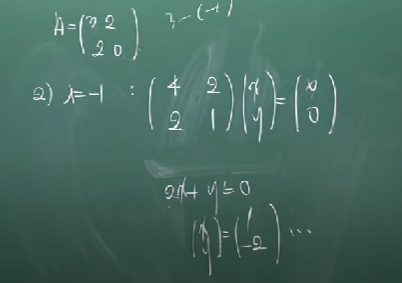
예제 2.
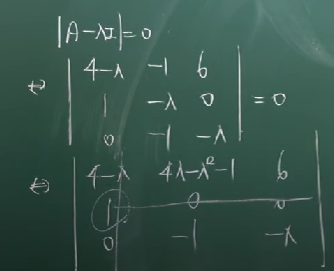
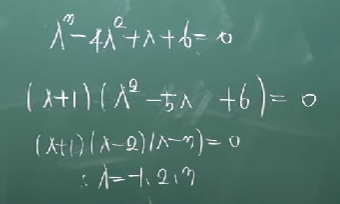
예제 3.
예제 4.
예제 5.
예제 6.
veloger