# 랭크(Rank)
행렬의 랭크는 행렬이 나타낼 수 있는 벡터 공간에서 기저의 개수를 의미하고, 이 기저는 서로 독립인 행또는 열의 벡터의 개수에 의해서 결정된다. 열과 행의 랭크는 서로 같은 값을 가지므로, 행렬의 랭크를 구할 때에는 한쪽의 랭크만 계산하면 되고, 서로 선형 독립인 벡터가 몇 개가 되는지만 확인하면 된다.
# 랭크의 연산 => 연립방정식 풀이 과정의 성질과 동일함.
ex) x-y = 4, 2x-y = -1 => 가감법 / 대입법
행렬식의 경우 위 아래 행을 바꾸거나 실수배를 해주면 결과 값이 달라지지만, 선형방정식을 풀이할 때는 상관이 없다.
랭크는 선형방정식의 성질을 따른다.
=> 위의 식: 계수행렬 / 아래 식: 확대 행렬
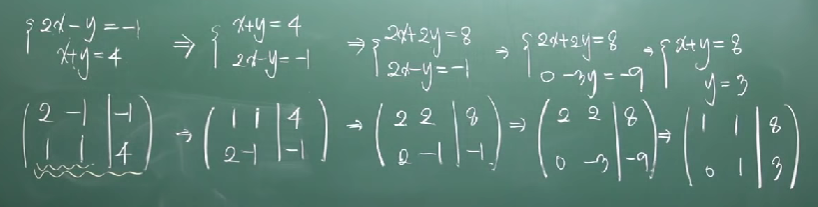
따라서, 랭크 연산에서는
1. 한 행의 실수배를 다른 행에 더하거나 빼도 된다.
2. 각 행의 위치를 서로 바꿔도 된다.
3. 열작업은 불가, 행작업만 가능하다.(행을 공배수로 약분 가능, 0위의 선두 원소는 0이 되면 안됨.)
4. 가우스 소거법 (첫번째 행의 선두 밑에는 모두 0으로 만드는 작업)
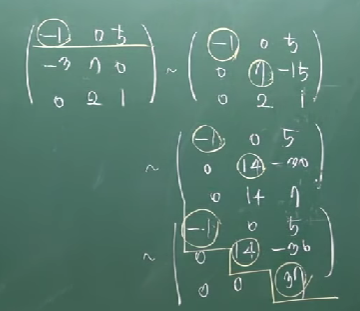
# 결론: 랭크 = 0이 아닌 행의 개수
# 예제
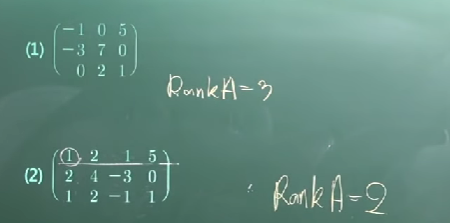
더 많은 Rank에 관한 정의
A라는 행렬의 Column rank는 Column space의 차원을 의미하고 Row rank는 Row space의 차원을 의미한다. 결국 행에서 선형 독립인 벡터의 개수와 열에서 선형 독립인 벡터의 개수를 구분해서 정의하겠다는 소리다.
Full rank
Full Rank는 다름이 아니라, 해당 행렬이 가질 수 있는 최대로 가능한 Rank의 값이 되겠다. 그런데 앞서 말했듯이, 행과 열의 각각의 Rank는 서로 같은 값을 가진다고 하였으므로, 아래와 같이 어느 한 쪽에서 작은 값의 사이즈가 Full Rank의 값이 된다.
예시
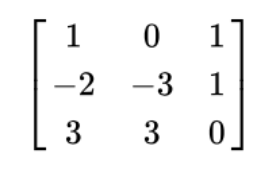
위의 행렬의 경우 랭크는 2이다. 왜냐하면, 첫 번째와 두 번째 열은 서로 선형 독립 관계에 있다고 볼 수 있다. 하지만, 세 번째 열의 경우에는 첫 번째 열에서 두 번째 열을 빼주게 되면 세 번째 열이 된다. 즉, 선형적으로 의존적인 관계가 성립한다. 따라서, 이 행렬의 Rank는 2가 된다.
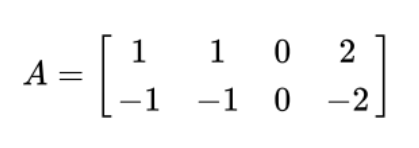
이 경우에도 마찬가지로, 행이든 열이든 하나만 보면 된다. 왜냐하면 이 둘의 랭크는 같은 값을 가질 것이기 때문이다. 위의 행렬의 경우에는 0을 제외 하고 나머지들은 서로 모두 의존적이다. 첫 번째 열은 정확히 두 번째 열과 같고, 네 번째 열은 첫 번째 열의 두 배와 정확히 같기 때문이다. 그런데 세 번째 열이 0의 값을 가지므로, 랭크에서는 제외되지만, 결국 세 번째 열을 제외한 나머지 세 개의 열들은 하나의 기저로 역할을 할 수 있으므로, 하나의 랭크를 가진다고 볼 수 있겠다. 따라서, 위의 행렬의 랭크는 1이다.
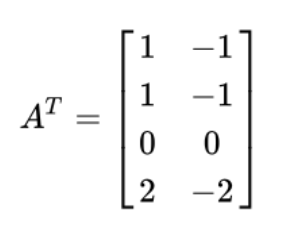
앞의 A행렬의 전치 행렬에 대해서 랭크를 구해보자. 여기서 보면, 열만 보게 되면 두 열은 서로 의존적이라는 것을 쉽게 알 수 있다. 왜냐하면 첫 번째 열에 마이너스 1을 곱하게 되면 두 번째 열이 되기때문이다. 그러므로, 결국 이 벡터 공간을 지배하는 기저는 하나라고 볼 수 있다. 비록 서로 의존적이지만, 이 두 벡터가 하나의 기저로서 작용할 수 있기 때문이다.