여러 개의 방정식이 주어졌을 때 연립 방정식으로 해 (solution)를 구하는 방법을 배웠을 것이다.
행렬을 이용하면 연립방적식의 해를 쉽게 구할 수 있는데, 이때 연립 방정식은 다른 말로 선형 시스템이라고도 한다.
본 페이지에서는 선형 방정식과 선형 시스템, 동차 선형 시스템에 대해 알아보려고 한다.
선형 방정식 (linear equation)
정의: 변수 x, y에 대한 1차 방정식으로 최고차항의 차수가 1인 방정식이다.
선형 방정식의 예
2x + 4y = 8
선형 방정식이 아닌 경우
y = cosx
x + y**1/2 = 2
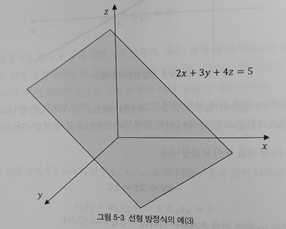
선형 시스템 (linear system)
x + 2y = 8
-2x + 4y = 8
정의: 위와 같은 선형 방정식이 다수 존재하는 경우, 선형 방정식의 집합을 연립 1차 방정식 (system of linear equation) 혹은 선형 시스템 (linear system)이라고 부른다.
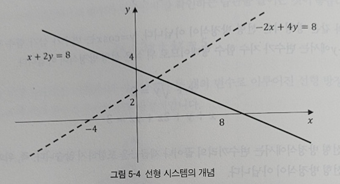
위에서 선형 시스템을 만족시키는 해 (solution)는 두 직선이 만나는 지점에 해당한다.
이 선형시스템이 해를 갖는 경우는 다음 세가지 경우 뿐이고, 항상 선형시스템이 해를 갖는 것은 아니다.
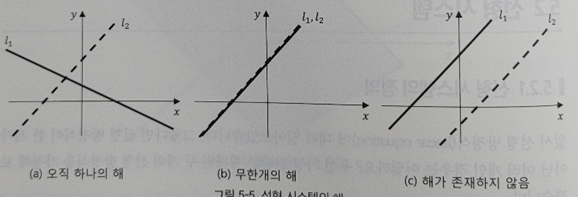
계수 행렬 (coefficient matrix)
- 선형연립방정식의 계수 만으로 이루어진 행렬
- 통상, 선형 연립방정식을 Ax=b 로 나타낼 때, 행렬 A를 말한다.
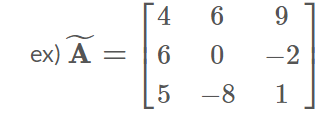
첨가 행렬 (확장행렬; 확대행렬; augmented matrix)
- 계수행렬 및 우변 상수항을 모두 포함한 행렬
- 계수행렬 및 우변 상수항을 모두 포함한 행렬
- 각 행이 선형연립방정식의 하나의 식과 대응되는 행렬
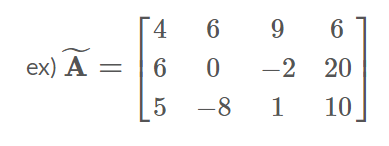
a11x1 + a12x2 + ... + a1pxp = b1
a11x1 + a22x2 + ... + a2pxp = b2
...
an1x1 + an2x2 + ... + anpxp = bn
위와 같은 선형 시스템의 상수 부분만 모아서 행렬 형태로 나타낸 것을 "첨가 행렬"이라고 한다.
=> 첨가행렬을 이용하면 선형 시스템의 해를 보다 쉽게 구할 수 있다.
벡터
- 단 하나의 행, 또는 하나의 열만으로 이루어진 행렬
- 벡터의 성분을 성분(component)라 한다.
- 벡터는 소문자 볼드체 문자 a,b,c,⋯, 또는 a=[aj]로 표현한다.
행벡터(Row Vector)
하나의 행으로 구성된 행렬
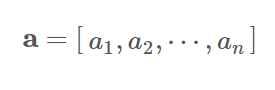
열벡터 (Column Vector)
하나의 열로 구성된 행렬
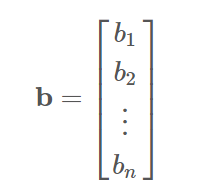
기본 행 연산 (elementary row operation)
- 한 행에 영이 아닌 상수를 "모두 곱한다"(=한 행에 모든 원소에 한해서만)
- 두 행을 교환한다.
- 한 행의 배수를 다른 행에 더한다.
기약행사다리꼴 (RREF, Reduced Row Echelon Form)
아래와 같이 해가 주어져 있는 확장행렬이 대표적인 기약행사다리꼴의 예시이다.
[기약행사다리꼴 예시]
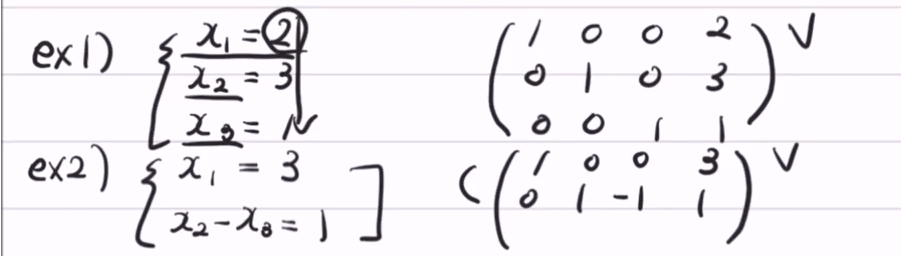

규칙 1. 영행이 아니라면, 각 행에서 처음 등장하는 영이 아닌 수는 1이고, 이를 leading 1이라고 부른다.
두번째 행렬과 같이 모두 0인 행이 존재하는 행렬은 우측의 2행, 3행과 같이 배수를 곱헸을 때 완전히 같아 상쇄되는 행렬이다.
규칙 2. 영행은 항상 맨 아래에 모여있다.
규칙 3. leading 1의 위치는 항상 한칸 이상 뒤로 밀린다.
규칙 4. leading 1이 포함된 열은 leading 1을 제외하면 모두 0이다.