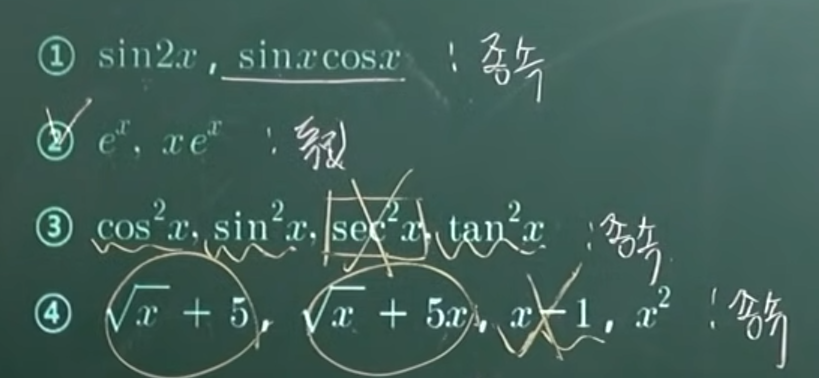일차 종속과 독립
1. 일차결합
정의 : 벡터 공간 V의 원소 v1,v2,v3...vn에 대하여 a1,a2,a3,...an이 임의의 실수일 때, a1v1+a2v2+a3v3+...anvn을 v1,v2,v3...vn의 일차 결합이라 한다.
일차결합으로 인한 최종 결과값(계산된 값) = 생성
벡터공간 V의 부분집합 {v1,v2,v3...vn}과 임의의 실수 a1,a2,a3,...an에 대해, a1v1+a2v2+a3v3+...anvn = 0이라 할 때, a1,a2,a3,...an 에 따라 일차독립 또는 일차 종속으로 구분된다.
- 일차(선형)독립
a1 = a2 = a3 = ... = an = 0이면 {v1, v2, ..., vn}은 일차독립이다.
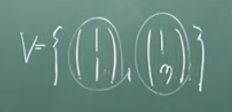
- 일차(선형)종속
a1,a2,a3,...an 중에 적어도 하나 0이 아닌 것이 존재할 때, {v1, v2, ..., vn}은 일차종속이다.
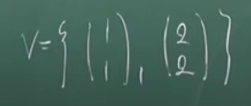
=> "실수배"를 하여 다른 원소가 될 수 있으면 이는 일차종속에 해당한다.
(실수 = 상수)
참고) 삼각함수의 반각, 배각 공식
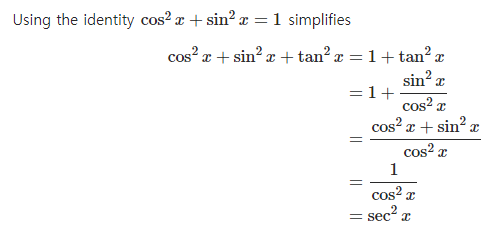
Ex 1)
Ex 2)
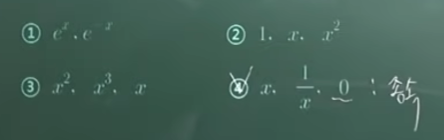
Ex 3)
veloger